【精品试卷】人教版 七年级下册数学 第09章 章末检测(含答案)
第九章 不等式与不等式组
章末检测
(时间:90 分钟 满分:120 分)
一、选择题(本大题共 10 小题,每小题 3 分,共 30 分.在每小题给出的四个选项中,只有一个选项是符
合题目要求的)
1.不等式 x+1>3 的解集是
A.x>1 B.x>–2 C.x>2 D.x<2
2.在数轴上表示不等式 x–1≤0 的解集,正确的是
A. B.
C. D.
3.x 与 3 的和的一半是负数,用不等式表示为
A. 1
2 x+3>0 B. 1
2 x+3<0
C. 1
2 (x+3)<0 D. 1
2 (x+3)>0
4.下列说法中,错误的是
A.x=1 是不等式 x<2 的解
B.–2 是不等式 2x–1<0 的一个解
C.不等式–3x>9 的解集是 x=–3
D.不等式 x<10 的整数解有无数个
5.若– 1
2 a≥b,则 a≤–2b,其根据是
A.不等式的两边加(或减)同一个数(或式子),不等号的方向不变
B.不等式的两边乘(或除以)同一个正数,不等号的方向不变
C.不等式的两边乘(或除以)同一个负数,不等号的方向改变
D.以上答案均不对
6.下列不等式中,不含有 1x 这个解的是
A. 2 1 3x B. 2 1 3x
C. 2 1 3x D. 2 1 3x
7.不等式组
1 1 32
2 3 0
x
x x
的最大整数解为
A.8 B.6 C.5 D.4
8.关于 x 的不等式组 3 1 4 1x x
x m
的解集为 x<3,那么 m 的取值范围为
A.m=3 B.m>3 C.m<3 D.m≥3
9.一次智力测验,有 20 道选择题.评分标准是:对 1 题给 5 分,错 1 题扣 2 分,不答题不给分也不扣分.小
明有两道题未答.至少答对几道题,总分才不会低于 60 分?则小明至少答对的题数是
A.11 道 B.12 道 C.13 道 D.14 道
10.阅读理解:我们把 a b
c d
称作二阶行列式,规定它的运算法则为 a c ad bcb d
,例如 1 3
2 4
=1 4 2 3= 2 ,如果 2 3
1
x
x
0 ,则 x 的取值范围是
A.x>1 B.x<–1 C.x>3 D.x<–3
二、填空题(本大题共 10 小题,每小题 3 分,共 30 分)
11.如果 1
”、“<”或“=”)
12.写出一个解集为 x<–1,且未知数的系数为 2 的一元一次不等式:__________.
13.当 x__________时,式子–2(x–1)的值小于 8.
14.不等式组 1 0
2 3
x
x x
的解集是__________.
15.不等式 2x+5>4x–1 的正整数解是__________.
16.一件商品的进价是 500 元,标价为 600 元,打折销售后要保证获利不低于 8%,则此商品最少打__________
折.
17.某商品的售价是 528 元,商家出售一件这样的商品可获利润是进价的 10%~20%,设进价为 x 元,则 x
的取值范围是__________.
18.已知关于 x 的不等式组 1 2 6
3 4
x
x a
只有两个整数解,则 a 的取值范围__________.
19. 2x 的最小值是 a, 6x 的最大值是 b,则 a+b=__________.
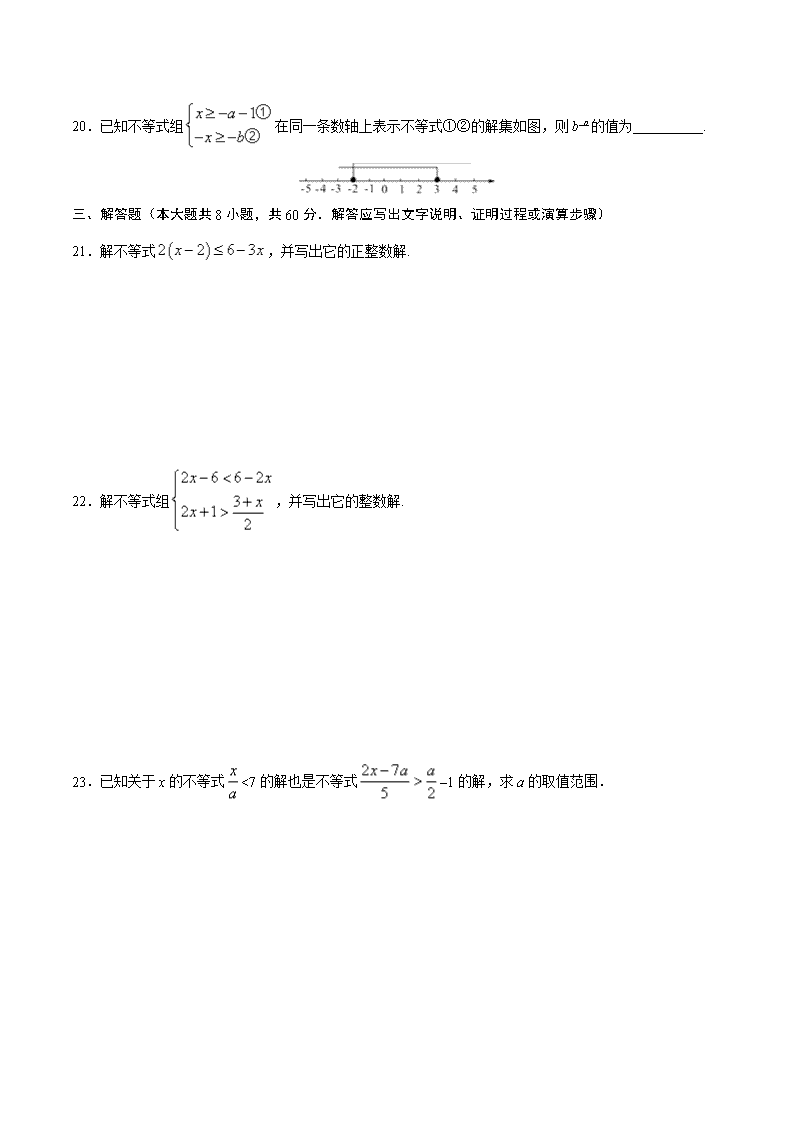
20.已知不等式组 1x a
x b
①
② 在同一条数轴上表示不等式①②的解集如图,则 b–a 的值为__________.
三、解答题(本大题共 8 小题,共 60 分.解答应写出文字说明、证明过程或演算步骤)
21.解不等式 2 2 6 3x x ,并写出它的正整数解.
22.解不等式组
2 6 6 2
32 1 2
x x
xx
,并写出它的整数解.
23.已知关于 x 的不等式 x
a <7 的解也是不等式 2 7
5 2
x a a –1 的解,求 a 的取值范围.
24.解不等式组:
2 6
2
3 1 1
x
x
x x
①
②
③
.
请结合题意,完成本题的解答.
(1)解不等式①,得__________,依据是:__________.
(2)解不等式③,得__________.
(3)把不等式①,②和③的解集在数轴上表示出来.
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集.
25.根据等式和不等式的基本性质,我们可以得到比较两数大小的方法:
(1)若 a–b>0,则 a__________b;
(2)若 a–b=0,则 a__________b;
(3)若 a–b<0,则 a__________b.
这种比较大小的方法称为“求差法比较大小”.
请运用这种方法尝试解决下面的问题:
比较 4+3a2–2b+b2 与 3a2–2b+1 的大小.
26.分子、分母都是整式,并且分母中含有未知数的不等式叫做分式不等式.
小亮在解分式不等式 2 5
3
x
x
>0 时,是这样思考的:
根据“两数相除,同号得正,异号得负”,原分式不等式可转化为下面两个不等式组:
① 2 5 0
3 0
x
x
或② 2 5 0
3 0
x
x
,
解不等式组①,得 x>3,
解不等式组②,得 x<– 5
2 .
所以原分式不等式的解集为 x>3 或 x<– 5
2 .
请你参考小亮思考问题的方法,解分式不等式 3 4
2
x
x
<0.
27.如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程.
(1)在方程①3x–1=0,② 2 1 03 x ,③x–(3x+1)=–5 中,不等式组 2 5
3 1 2
x x
x x
的关联方程是
________;
(2)若不等式组
1 12
1 3 2
x
x x
的一个关联方程的根是整数,则这个关联方程可以是________(写出
一个即可);
(3)若方程 3–x=2x,3+x= 12 2x
都是关于 x 的不等式组 2
2
x x m
x m
的关联方程,直接写出 m 的
取值范围.
28.为降低空气污染,启东飞鹤公交公司决定全部更换节能环保的燃气公交车.计划购买 A 型和 B 型两种
公交车共 10 辆,其中每台的价格,年载客量如表:
A 型 B 型
价格(万元/台) a b
年载客量(万人/年) 60 100
若购买 A 型公交车 1 辆,B 型公交车 2 辆,共需 400 万元;若购买 A 型公交车 2 辆,B 型公交车 1 辆,
共需 350 万元.
(1)求 a,b 的值;
(2)如果该公司购买 A 型和 B 型公交车的总费用不超过 1200 万元,且确保这 10 辆公交车在该线路的
年均载客量总和不少于 680 万人次.请你设计一个方案,使得购车总费用最少.
1.【答案】C
【解析】移项,得 x>3–1,合并同类项,得 x>2.故选 C.
2.【答案】D
【解析】∵x–1≤0,∴x≤1,∴在数轴上可表示为: ,故选 D.
3.【答案】C
【解析】“ x 与 3 的和的一半是负数”用不等式表示为: 1 3 02 x .故选 C.
4.【答案】C
【解析】A、B、D 正确,C.不等式–3x>9 的解集是 x<–3.故选 C.
5.【答案】C
【解析】∵把– 1
2 a≥b 的两边都除以– 1
2
,可得 a≤–2b,∴其根据是:不等式的两边乘(或除以)同一个负
数,不等号的方向改变.故选 C.
6.【答案】A
【解析】由不等式 2x+1<–3 可得 x<–2,所以 x=–1 不是不等式 2x+1<–3 的解;
由 2x–1≥–3 的解集为 x≥–1,可知 x=–1 是不等式 2x+1≥–3 的解;
由–2x+1≥3 的解集为 x≤–1,可知 x=–1 是不等式–2x+1≥3 的解;
由–2x–1≤3 的解集为 x≥–2,可知 x=–1 是不等式–2x–1≤3 的解.
故选 A.
7.【答案】C
【解析】解不等式组
1 1 32
2 3 0
x
x x
得 –8 6x ,所以最大整数解为 5.故选 C.
8.【答案】D
【解析】不等式组变形得: 3x
x m
,由不等式组的解集为 x<3,得到 m 的取值范围为 m≥3,故选 D.
9.【答案】D
【解析】设小明至少答对的题数是 x 道,由题可得 5x–2(20–2–x)≥60,解得 x≥13 5
7
,故答对的题数至
少应为 14.故选 D.
10.【答案】A
【解析】由题意可得 2x−(3−x)>0,解得 x>1.故选 A.
11.【答案】<
【解析】因为 10,x–2<0,(x–1)(x–2)<0,故答案为:<.
12.【答案】2x<–2(答案不唯一)
【解析】两边都乘以 2,得:2x<–2(答案不唯一).故答案为:2x<–2(答案不唯一).
13.【答案】>–3
【解析】由题意得:–2(x–1)<8,整理得:–2x+2<8,移项得:–2x<8–2,合并同类项得:–2x<6,系
数化为 1 得:x>–3.故答案为:>–3.
14.【答案】 3 1x
【解析】 1 0
2 3
x
x x
①
② ,
∵解不等式①得:x<1,解不等式②得:x>−3,
∴不等式组的解集为:−3–1–5,
合并同类项,得:–2x>–6,
系数化成 1 得:x<3.
则正整数解是:1,2.
故答案是:1,2.
16.【答案】9
【解析】设可以打 x 折.那么(600×10
x –500)÷500≥8%,解得 x≥9.
故答案为:9.
17.【答案】440≤x≤480
【解析】根据:售价=进价×(1+利润率),可得:进价=
1
售价
利润率 ,商品可获利润(10%~20%),
即售价至少是进价(1+10%)倍,最多是进价的 1+20%倍,据此可到不等式组:
528
1 20% ≤x≤ 528
1 10%
,解得 440≤x≤480.∴x 的取值范围是 440≤x≤480.故答案为:440≤x≤480.
18.【答案】4– 12 2
,由②得 x≤ 4
3
a ,∴– 12 2 3
2
x 得: 1
3x .
∴不等式组的解集为 1 33 x .
又 x 为整数,∴x=1,2.
∴原不等式组的整数解为 1,2.
23.【解析】解不等式 2 7 15 2
x a a > ,得:x 19 5
4 2a > .
∵关于 x 的不等式 x
a
7 的解也是不等式 2 7 15 2
x a a > 的解,故 a<0,
所以不等式 x
a
7 的解集是 x>7a.
所以 7a 19 5
4 2a ,解得:a 10
9
.
∵a<0,∴ 10
9
a<0.
24.【解析】(1)解不等式①,得 x≥–3,依据是:不等式的性质 3,
故答案为:x≥–3;不等式的性质 3;
(2)解不等式③,得 x<2,故答案为:x<2;
(3)把不等式①,②和③的解集在数轴上表示出来,如图所示:
(4)从图中可以找出三个不等式解集的公共部分,得不等式组的解集为:–20,所以 a–b+b>0+b,即 a>b;
(2)因为 a–b=0,所以 a–b+b=0+b,即 a=b;
(3)因为 a–b<0,所以 a–b+b<0+b,即 a0,所以 4+3a2–2b+b2>3a2–2b+1.
26.【解析】根据“两数相除,同号得正,异号得负”,原分式不等式可转化为下面两个不等式组:
① 3 4 0
2 0
x
x
或② 3 4 0
2 0
x
x
,
解不等式组①,得 4
3
查看更多