- 2021-10-25 发布 |
- 37.5 KB |
- 17页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
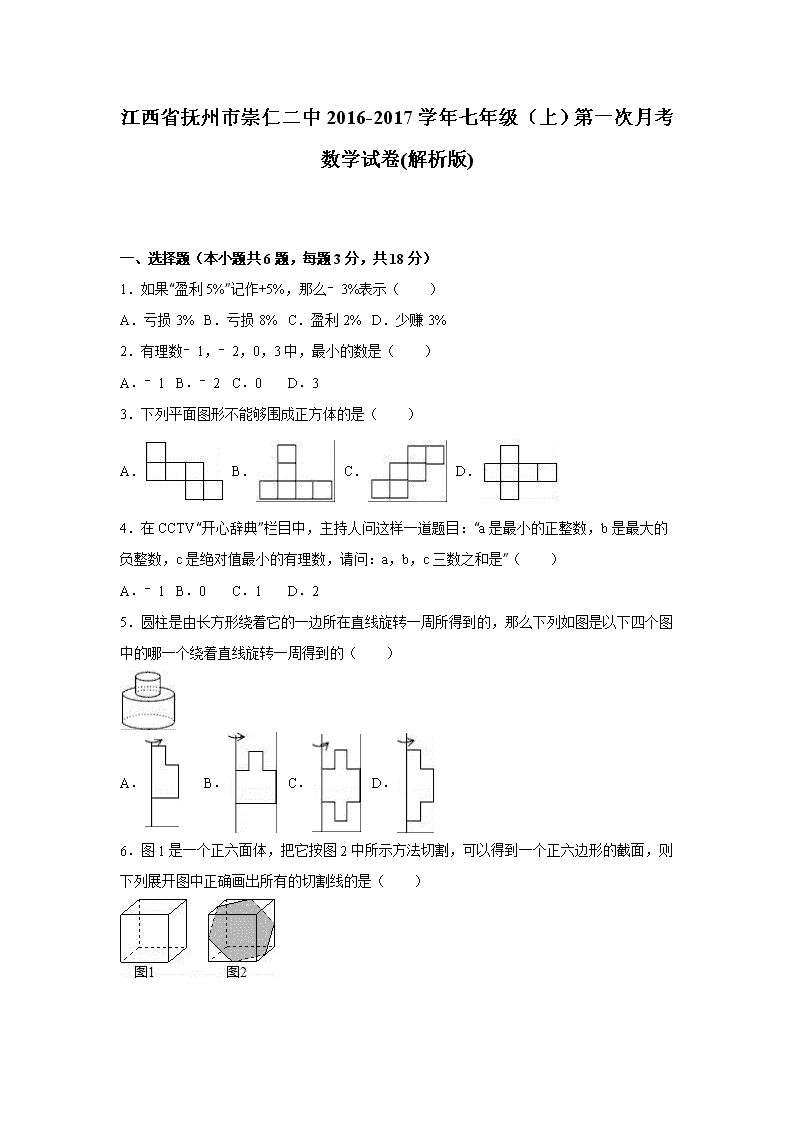
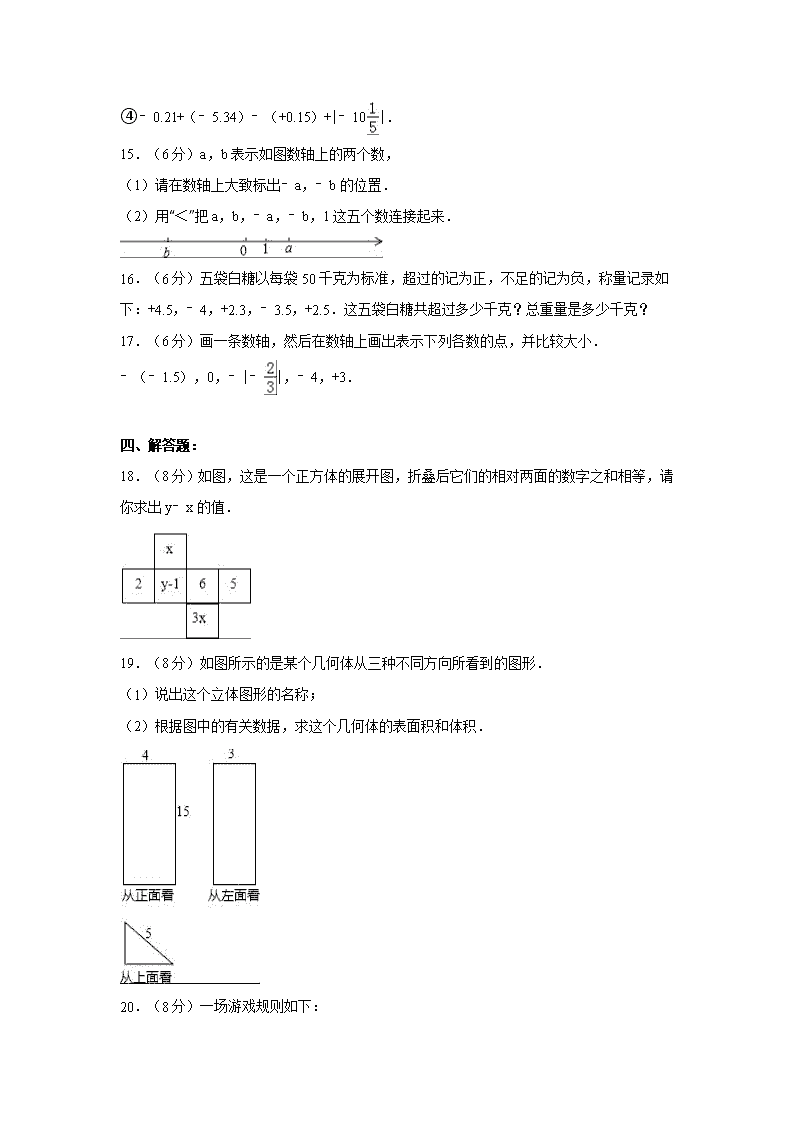
七年级上第一次月考数学试卷含答案解析 (2)
江西省抚州市崇仁二中2016-2017学年七年级(上)第一次月考数学试卷(解析版) 一、选择题(本小题共6题,每题3分,共18分) 1.如果“盈利5%”记作+5%,那么﹣3%表示( ) A.亏损3% B.亏损8% C.盈利2% D.少赚3% 2.有理数﹣1,﹣2,0,3中,最小的数是( ) A.﹣1 B.﹣2 C.0 D.3 3.下列平面图形不能够围成正方体的是( ) A. B. C. D. 4.在CCTV“开心辞典”栏目中,主持人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是”( ) A.﹣1 B.0 C.1 D.2 5.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列如图是以下四个图中的哪一个绕着直线旋转一周得到的( ) A. B. C. D. 6.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是( ) A. B. C. D. 二、填空题(本小题共6题,每题3分,共18分) 7.飞机表演的“飞机拉线”用数学知识解释为: . 8.数轴上的一点由+3出发,向左移动4个单位,又向右移动了5个单位,两次移动后,这一点所表示的数是 . 9.用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是 . 10.写出一个从上面看与从正面看完全相同的几何体 . 11.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块. 12.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 . 三、解答题(共36分) 13.(6分)将下列各数填在相应的括号里: 3、﹣7、﹣、5.6、0、﹣8、15、 分数集合:{ } 整数集合:{ } 非负数集合:{ }. 14.(12分)计算: ①(﹣9)﹣(﹣7)+(﹣6)﹣(+4)﹣(﹣5); ②﹣14+11﹣(﹣12)﹣14+(﹣11); ③4﹣(+3.85)﹣(﹣3)+(﹣3.15); ④﹣0.21+(﹣5.34)﹣(+0.15)+|﹣10|. 15.(6分)a,b表示如图数轴上的两个数, (1)请在数轴上大致标出﹣a,﹣b的位置. (2)用“<”把a,b,﹣a,﹣b,1这五个数连接起来. 16.(6分)五袋白糖以每袋50千克为标准,超过的记为正,不足的记为负,称量记录如下:+4.5,﹣4,+2.3,﹣3.5,+2.5.这五袋白糖共超过多少千克?总重量是多少千克? 17.(6分)画一条数轴,然后在数轴上画出表示下列各数的点,并比较大小. ﹣(﹣1.5),0,﹣|﹣|,﹣4,+3. 四、解答题: 18.(8分)如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和相等,请你求出y﹣x的值. 19.(8分)如图所示的是某个几何体从三种不同方向所看到的图形. (1)说出这个立体图形的名称; (2)根据图中的有关数据,求这个几何体的表面积和体积. 20.(8分)一场游戏规则如下: (1)每人每次抽4张卡片,如果抽到形如的卡片,那么加上卡片上的数字,如果抽到形如的卡片,那么减去卡片上的数字; (2)比较两人所抽到的4张卡片的计算结果,结果大的为胜者. 请你通过计算(要求有计算过程)回答本次游戏获胜的是谁? 小亮抽到的卡片如图所示: 小丽抽到的卡片如图所示: 21.(8分)教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):+5,﹣4,﹣8,+10,+3,﹣6,+7,﹣11. (1)将最后一名老师送到目的地时,小王距出发地多少千米?方位如何? (2)若汽车耗油量为0.2升/千米,则当天耗油多少升?若汽油价格为5.70元/升,则小王共花费了多少元钱? 五、解答题: 22.(8分)已知a是最大的负整数的相反数,|b+4|=2,且|c﹣5|+|d+3|=0, (1)写出a、b、c、d的值. (2)计算a﹣b﹣c+d的值. 23.(10分)小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体. (1)请画出可能得到的几何体简图. (2)分别计算出这些几何体的体积.(锥体体积=底面积×高) 2016-2017学年江西省抚州市崇仁二中七年级(上)第一次月考数学试卷 参考答案与试题解析 一、选择题(本小题共6题,每题3分,共18分) 1.如果“盈利5%”记作+5%,那么﹣3%表示( ) A.亏损3% B.亏损8% C.盈利2% D.少赚3% 【考点】正数和负数. 【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答. 【解答】解:∵盈利5%”记作+5%, ∴﹣3%表示表示亏损3%. 故选:A. 【点评】此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示. 2.有理数﹣1,﹣2,0,3中,最小的数是( ) A.﹣1 B.﹣2 C.0 D.3 【考点】有理数大小比较. 【分析】先求出|﹣1|=1,|﹣2|=2,根据负数的绝对值越大,这个数就越小得到﹣2<﹣1,而0大于任何负数,小于任何正数,则有理数﹣1,﹣2,0,3的大小关系为﹣2<﹣1<0<3. 【解答】解:∵|﹣1|=1,|﹣2|=2, ∴﹣2<﹣1, ∴有理数﹣1,﹣2,0,3的大小关系为﹣2<﹣1<0<3. 故选B. 【点评】本题考查了有理数的大小比较:0大于任何负数,小于任何正数;负数的绝对值越大,这个数就越小. 3.下列平面图形不能够围成正方体的是( ) A. B. C. D. 【考点】几何体的展开图. 【分析】直接利用正方体的表面展开图特点判断即可. 【解答】解:根据正方体展开图的特点可判断A、D属于“1,4,1”格式,能围成正方体,C、属于“2,2,2”的格式也能围成正方体,B、不能围成正方体. 故选B. 【点评】主要考查了正方体的表面展开图. 4.在CCTV“开心辞典”栏目中,主持人问这样一道题目:“a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,请问:a,b,c三数之和是”( ) A.﹣1 B.0 C.1 D.2 【考点】有理数的加法;绝对值. 【分析】先求出a,b,c的值,再把它们相加即可. 【解答】解:由题意,得:a=1,b=﹣1,c=0, 故a+b+c=1﹣1+0=0. 故选B. 【点评】此题主要考查的是绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0. 5.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列如图是以下四个图中的哪一个绕着直线旋转一周得到的( ) A. B. C. D. 【考点】点、线、面、体. 【分析】分别根据各选项分析得出几何体的形状进而得出答案. 【解答】解:A、可以通过旋转得到两个圆柱,故本选项正确; B、可以通过旋转得到一个圆柱,一个圆筒,故本选项错误; C、可以通过旋转得到一个圆柱,两个圆筒,故本选项错误; D、可以通过旋转得到三个圆柱,故本选项错误. 故选:A. 【点评】此题主要考查了点、线、面、体,根据基本图形旋转得出几何体需要同学们较好的空间想象能力. 6.图1是一个正六面体,把它按图2中所示方法切割,可以得到一个正六边形的截面,则下列展开图中正确画出所有的切割线的是( ) A. B. C. D. 【考点】截一个几何体;几何体的展开图. 【分析】根据正六面体和截面的特征,可动手操作得到答案. 【解答】解:动手操作可知,画出所有的切割线的是图形C. 故选C. 【点评】考查了截一个几何体和几何体的展开图,观察思考与动手操作结合,得到相应的规律是解决本题的关键. 二、填空题(本小题共6题,每题3分,共18分) 7.飞机表演的“飞机拉线”用数学知识解释为: 点动成线 . 【考点】点、线、面、体. 【分析】飞机在空中表演,飞机可看作一个点,则“飞机拉线”用数学知识解释为:点动成线. 【解答】解:飞机表演的“飞机拉线”用数学知识解释为:点动成线. 故答案为点动成线. 【点评】本题考查了点、线、面、体的关系,从运动的观点来看,点动成线,线动成面,面动成体.点、线、面、体组成几何图形,点、线、面、体的运动组成了多姿多彩的图形世界. 8.数轴上的一点由+3出发,向左移动4个单位,又向右移动了5个单位,两次移动后,这一点所表示的数是 4 . 【考点】数轴;有理数的加减混合运算. 【分析】分别求出每次移动后的各个数,利用数轴即可表示. 【解答】解: +3向左移动4个单位长度,到达A,表示﹣1,﹣1向右移动了5个单位,就到达B,表示4. 【点评】借助数轴用几何方法化简含有绝对值的式子,比较有关数的大小有直观、简捷,举重若轻的优势. 9.用一个平面截长方体、五棱柱、圆柱和圆锥,不能截出三角形的是 圆柱 . 【考点】截一个几何体. 【分析】当截面的角度和方向不同时,圆柱体的截面无论什么方向截取圆柱都不会截得三角形. 【解答】解:长方体沿体面对角线截几何体可以截出三角形; 五棱柱沿顶点截几何体可以截得三角形; 圆柱不能截出三角形; 圆锥沿顶点可以截出三角形. 故不能截出三角形的几何体是圆柱. 故答案为:圆柱. 【点评】本题考查几何体的截面,截面的形状既与被截的几何体有关,还与截面的角度和方向有关. 10.写出一个从上面看与从正面看完全相同的几何体 正方体 . 【考点】简单几何体的三视图. 【分析】分别根据所看位置写出每个几何体的三视图形状,即可得到答案. 【解答】解:正方体从正面看,上面看得到的平面图形都是正方形, 则这个几何体的形状是正方体; 故答案为:正方体. 【点评】本题考查了几何体的三种视图,掌握定义是关键.注意所有的看到的棱都应表现在三视图中. 11.如图:在桌上摆有一些大小相同的正方体木块,其从正面和从左面看到的形状图如图所示,则要摆出这样的图形至少需要 6 块正方体木块,至多需要 16 块正方体木块. 【考点】由三视图判断几何体. 【分析】利用从正面和从左面看到的形状图进而得出每层的最少与最多数量,进而得出答案. 【解答】解:易得第一层最少有4个正方体,最多有12个正方体;第二层最少有2个正方体,最多有4个,故最少有6个小正方形,至多要16块小正方体. 故答案为:6,16. 【点评】此题考查由三视图探究几何体.可从主视图上分清物体的上下和左右的层数,从左视图上分清物体的左右和前后位置,综合上述条件,可知摆出图形至少以及至多要多少块木块. 12.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积等于 144或384π . 【考点】几何体的展开图. 【分析】分两种情况:①底面周长为6高为16π;②底面周长为16π高为6;先根据底面周长得到底面半径,再根据圆柱的体积公式计算即可求解. 【解答】解:①底面周长为6高为16π, π×()2×16π =π××16π =144; ②底面周长为16π高为6, π×()2×6 =π×64×6 =384π. 答:这个圆柱的体积可以是144或384π. 故答案为:144或384π. 【点评】本题考查了展开图折叠成几何体,本题关键是熟练掌握圆柱的体积公式,注意分类思想的运用. 三、解答题(共36分) 13.将下列各数填在相应的括号里: 3、﹣7、﹣、5.6、0、﹣8、15、 分数集合:{ ﹣,5.6,﹣8, } 整数集合:{ 3,﹣7,0,15 } 非负数集合:{ 3,5.6,0,15, }. 【考点】有理数. 【分析】利用分数,整数,以及非负数的定义判断即可. 【解答】解:分数集合:{﹣,5.6,﹣8, };整数集合:{3、﹣7、0、15};非负数集合:{3,5.6,0,15, }, 故答案为:﹣,5.6,﹣8,;3、﹣7、0、15;3,5.6,0,15, 【点评】此题考查了有理数,弄清各自的定义是解本题的关键. 14.(12分)(2016秋•抚州校级月考)计算: ①(﹣9)﹣(﹣7)+(﹣6)﹣(+4)﹣(﹣5); ②﹣14+11﹣(﹣12)﹣14+(﹣11); ③4﹣(+3.85)﹣(﹣3)+(﹣3.15); ④﹣0.21+(﹣5.34)﹣(+0.15)+|﹣10|. 【考点】有理数的加减混合运算. 【分析】根据有理数的加减混合运算法则计算即可. 【解答】解:①(﹣9)﹣(﹣7)+(﹣6)﹣(+4)﹣(﹣5) =﹣9﹣6﹣4+7+5 =﹣19+12 =﹣7; ②﹣14+11﹣(﹣12)﹣14+(﹣11) =﹣14+12﹣14+(11﹣11) =﹣16; ③4﹣(+3.85)﹣(﹣3)+(﹣3.15) =4+3+(﹣3.85﹣3.15) =8﹣7 =1; ④﹣0.21+(﹣5.34)﹣(+0.15)+|﹣10| =﹣0.21﹣5.34﹣0.15+10.2 =4.5. 【点评】本题考查的是有理数的加减混合运算,掌握有理数的加减混合运算法则是解题的关键. 15.a,b表示如图数轴上的两个数, (1)请在数轴上大致标出﹣a,﹣b的位置. (2)用“<”把a,b,﹣a,﹣b,1这五个数连接起来. 【考点】有理数大小比较;数轴. 【分析】(1)根据相反数的定义,在数轴上进行表示; (2)根据数轴上右侧的数大于左侧的数,即可解答. 【解答】解:(1), (2)b<﹣a<1<a<﹣b 【点评】本题考查了有理数的大小比较,解决本题的关键是熟记正数大于负数和0,0大于负数,数轴上右侧的数大于左侧的数. 16.五袋白糖以每袋50千克为标准,超过的记为正,不足的记为负,称量记录如下:+4.5,﹣4,+2.3,﹣3.5,+2.5.这五袋白糖共超过多少千克?总重量是多少千克? 【考点】有理数的加法;正数和负数. 【分析】首先审清题意,明确“正”和“负”所表示的意义;再根据题意作答. 【解答】解:(1)白糖以每袋50千克为标准,超过的记为正,不足的记为负,称量记录如下:+4.5,﹣4,+2.3,﹣3.5,+2.5.这五袋白糖共超过(4.5﹣4+2.3﹣3.5+2.5)=1.8千克, 故这五袋白糖共超过1.8千克; (2)总重量是5×50+1.8=251.8千克, 故五袋白糖的总重量是251.8千克. 【点评】解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.一般情况下具有相反意义的量才是一对具有相反意义的量. 17.画一条数轴,然后在数轴上画出表示下列各数的点,并比较大小. ﹣(﹣1.5),0,﹣|﹣|,﹣4,+3. 【考点】有理数大小比较;数轴. 【分析】先画出数轴并在数轴上表示出各数,再按照数轴的特点从左到右用小于号把各数连接起来. 【解答】解:画出数轴并在数轴上表示出各数: 按照数轴的特点用小于号从左到右把各数连接起来为:﹣4<﹣|﹣|<0<﹣(﹣1.5)<+3. 【点评】本题考查的是有理数的大小比较,由于引进了数轴,我们把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想. 四、解答题: 18.如图,这是一个正方体的展开图,折叠后它们的相对两面的数字之和相等,请你求出y﹣x的值. 【考点】专题:正方体相对两个面上的文字. 【分析】利用正方体的表面展开图,相对的面之间一定相隔一个正方形,可得x+3x=2+6,y﹣1+5=2+6,解方程求出x与y的值,进而求解即可. 【解答】解:由题意,得x+3x=2+6,y﹣1+5=2+6, 解得x=2,y=4, 所以y﹣x=4﹣2=2. 【点评】本题考查了正方体相对两个面上的文字,注意正方体的空间图形,从相对面入手,分析及解答问题. 19.如图所示的是某个几何体从三种不同方向所看到的图形. (1)说出这个立体图形的名称; (2)根据图中的有关数据,求这个几何体的表面积和体积. 【考点】由三视图判断几何体;几何体的表面积. 【分析】(1)根据三视图可直接得出这个立体图形是三棱柱; (2)根据直三棱柱的表面积公式和闽籍公式分别进行计算即可. 【解答】解:(1)根据三视图可得:这个立体图形是三棱柱; (2)表面积为:×3×4×2+15×3+15×4+15×5=192; 体积是:×3×4×15=90; 【点评】本题主要考查由三视图确定几何体和求几何体的表面积等相关知识,同时也考查学生的空间想象能力. 20.一场游戏规则如下: (1)每人每次抽4张卡片,如果抽到形如的卡片,那么加上卡片上的数字,如果抽到形如的卡片,那么减去卡片上的数字; (2)比较两人所抽到的4张卡片的计算结果,结果大的为胜者. 请你通过计算(要求有计算过程)回答本次游戏获胜的是谁? 小亮抽到的卡片如图所示: 小丽抽到的卡片如图所示: 【考点】有理数的减法;有理数的加法. 【分析】分别计算后比较结果即可. 【解答】解:小亮所抽卡片上的数的和为:﹣(﹣)+(﹣5)﹣4=﹣7; 小丽所抽卡片上的数的和为:﹣2﹣(﹣)﹣5+(﹣)=﹣6; 因为﹣7<﹣6. 所以本次游戏获胜的是小丽. 【点评】本题考查了有理数的减法,注意加减混合运算应从左往右依次运算. 21.教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):+5,﹣4,﹣8,+10,+3,﹣6,+7,﹣11. (1)将最后一名老师送到目的地时,小王距出发地多少千米?方位如何? (2)若汽车耗油量为0.2升/千米,则当天耗油多少升?若汽油价格为5.70元/升,则小王共花费了多少元钱? 【考点】正数和负数. 【分析】(1)求出各个数的和,依据结果即可判断; (2)求出汽车行驶的路程即可解决. 【解答】解:(1)+5﹣4﹣8+10+3﹣6+7﹣11=﹣4. 则距出发地西边4千米; (2)汽车的总路程是:5+4+8+10+3+6+7+11=54千米, 则耗油是54×0.2=10.8升,花费10.8×5.70=61.56元, 答:当天耗油10.8升,小王共花费了61.56元. 【点评】此题考查了正数和负数,利用正负号可以分别表示向东和向西,就可以表示位置,在本题中注意不要用(1)中求得的数﹣4代替汽车的路程. 五、解答题: 22.已知a是最大的负整数的相反数,|b+4|=2,且|c﹣5|+|d+3|=0, (1)写出a、b、c、d的值. (2)计算a﹣b﹣c+d的值. 【考点】非负数的性质:绝对值;有理数. 【分析】(1)根据有理数的概念求出a的值,根据绝对值的性质求出b的值,再根据非负数的性质列方程求出c、d的值; (2)将a、b、c、d的值代入代数式进行计算即可得解. 【解答】解:(1)∵a是最大的负整数的相反数, ∴a=1, ∵|b+4|=2, ∴b+4=2或b+4=﹣2, ∴b=﹣2或b=﹣6, ∵|c﹣5|+|d+3|=0, ∴c﹣5=0,d+3=0, 解得c=5,d=﹣3, 所以,a=1,b=﹣2或﹣6,c=5,d=﹣3; (2)a﹣b﹣c+d=1﹣(﹣2)﹣5+(﹣3), =1+2﹣5﹣3, =﹣5, 或a﹣b﹣c+d=1﹣(﹣6)﹣5+(﹣3), =1+6﹣5﹣3, =﹣1, 所以,a﹣b﹣c+d的值为﹣5或﹣1. 【点评】本题考查了非负数的性质:几个非负数的和为0时,这几个非负数都为0. 23.(10分)(2016秋•抚州校级月考)小明学习了“面动成体”之后,他用一个边长为3cm、4cm和5cm的直角三角形,绕其中一条边旋转一周,得到了一个几何体. (1)请画出可能得到的几何体简图. (2)分别计算出这些几何体的体积.(锥体体积=底面积×高) 【考点】点、线、面、体. 【分析】(1)根据三角形旋转是圆锥,可得几何体; (2)根据圆锥的体积公式,可得答案. 【解答】解:(1)以4cm为轴,得 ; 以3cm为轴,得 ; 以5cm为轴,得 ; (2)以4cm为轴体积为×π×32×4=12π, 以3cm为轴的体积为×π×42×3=16π, 以5cm为轴的体积为×π()2×5=9.6π. 【点评】本题考查了点线面体,利用三角形旋转是圆锥是解题关键. 查看更多