- 2021-10-22 发布 |
- 37.5 KB |
- 17页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师版数学七年级下册课件-第8章-8 认识不等式
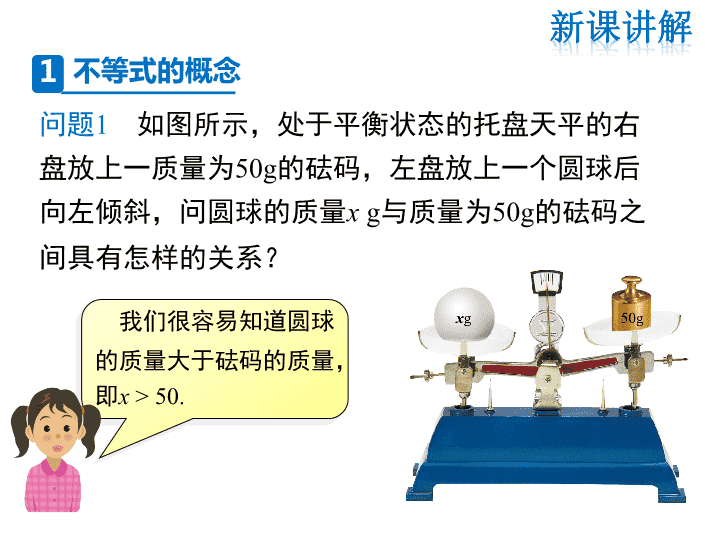
HS七(下) 教学课件 8.1 认识不等式 第8章 一元一次不等式 1.现实生活中,数量之间存在着相等与不相等的关系. 2.对于不相等的关系问题,我们如何用式子来表示 它们呢? 例如,小明的身高为155cm,小聪的身高为156cm, 则我们可以用不等号“>”或“<”来表示他们的 身高之间的关系. 如:156 > 155或155 < 156. 155cm 156cm 问题1 如图所示,处于平衡状态的托盘天平的右 盘放上一质量为50g的砝码,左盘放上一个圆球后 向左倾斜,问圆球的质量x g与质量为50g的砝码之 间具有怎样的关系? 我们很容易知道圆球 的质量大于砝码的质量, 即x > 50. 不等式的概念1 问题2 一辆轿车在一条规定车速应高于60km/h,且 低于100 km/h的高速公路上行驶,如何用式子来表 示轿车在该高速公路上行驶的路程s(km)与行驶时间 x(h)之间的关系呢? 根据路程与速度、时 间之间的关系可得: s>60x,且s<100x. 像156>155,155<156,x>50,s>60x,s<100x 这样,我们把用不等号“>”或“<”表示不等关系的式 子叫作不等式. 判断下列式子是不是不等式: (1)-3>0; (2)4x+3y<0; (3)x = 3; (4) x2+xy+y2; (5)x+2>y+5. 解 : (1)(2)(5)是不等式; (3)(4)不是不等式. 问题 公园的票价是:每人5元;一次购票满30张, 每张可少收1元。某班有27人去世纪公园进行活动。 当班长王小华准备好了零钱到售票处买27张票时, 爱动脑筋的李敏喊住了王小华,提议买30张票。但 有同学不明白,明明我们只有27个人,买30张票, 岂不是“浪费”吗? 那么,李敏的提议对不对呢?是不是真的浪费? 谈谈你们的看法。 2 不等式的解 买27张票,要付款 买30张票,要付款 显然 120<135 我们不妨一起来算一算 5×27=135(元) 4×30=120(元) 这就是说,买30张票比买27张票付款要少, 表面上看是“浪费”了3张票,而实际上节 省了。 如果去世纪公园的人数较少(例如10个人)显 然不值得去买30张票,还是按实际人数买票为好。 现在的问题是,少于30人时,至少有多少人去公园, 买30张票反而合算呢? 分析:设有x人进公园,如果x<30,那么按实际人数 要买 x张,付款5x(元),买30张票要付款 4×30=120(元),如果买30张票合算,那么应有 120<5x. 人数 (x) 按实际人数购票 的付款(元) (5x) 买团体票 的付款 (元) 120 买团体票 合算吗? (120<5x 成立吗?) 21 22 23 24 25 26 27 135 120 合算 成立 28 29 105 110 115 120 125 130 140 145 120 120 120 120 120 120 120 120 相等 合算 合算 合算 合算 (不成立) (不成立) (成立) (成立) (成立) (成立) 不合算 (不成立) 不合算 不合算 (不成立) 由 上 表 可 见 , 当 x = 2 5 , 2 6 , 2 7 , … , 时 , 不 等 式 120<5x成立,也就是说至少要x=25时不等式120<5x成立,即至少要有25人进公园时, 买30张票合算. 不等式120<5x中含有未知数x,能使不等式成立的 未知数的值,叫做不等式的解. 如上例中,x=25,26,27,…等都是120<5x的 解,而x=24,23,22,21则都不是不等式的解. 用不等式表示下列关系,并分别写出两个 满足不等式的数: (1)x的一半小于-1 ; (2)y与4的和大于0.5 ; (3)a是负数; (4)b是非负数. 例 解: (1) 0.5x <-1.如 x=-3,-4. (2) y+4>0.5. 如 y=0,1. (3) a<0 . 如a=-3,-4. (4) b是非负数,即b不是负数,它可以是正数 或零,即b>0或b=0.如b=0或2. 1. 用不等式表示下列数量关系: (1)a是负数; (2)x比-3小; (3)两数m与n的差大于5. a < 0. x < -3. m-n >5. 2.雷电的温度大约是28 000℃,比太阳表面温度的 4.5倍还要高.设太阳表面温度为t℃,那么t应该满 足怎样的关系式? 解:4.5t<28 000. 不等式 实际问题中不等式的表示 不等式 的解 概念查看更多