【北师大版】七年级下册数学第四章+三角形第3节《探索三角形全等的条件》第三课时参考课件2

【北师大版】七年级下册数学第四章+三角形第3节《探索三角形全等的条件》第三课时参考课件2

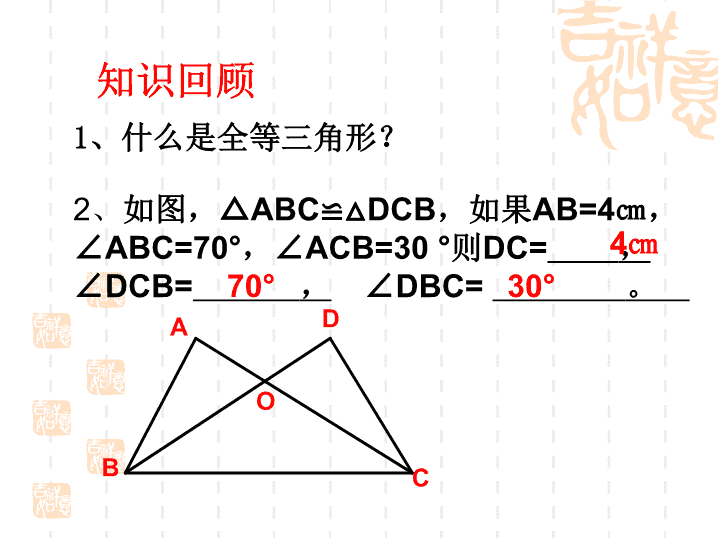
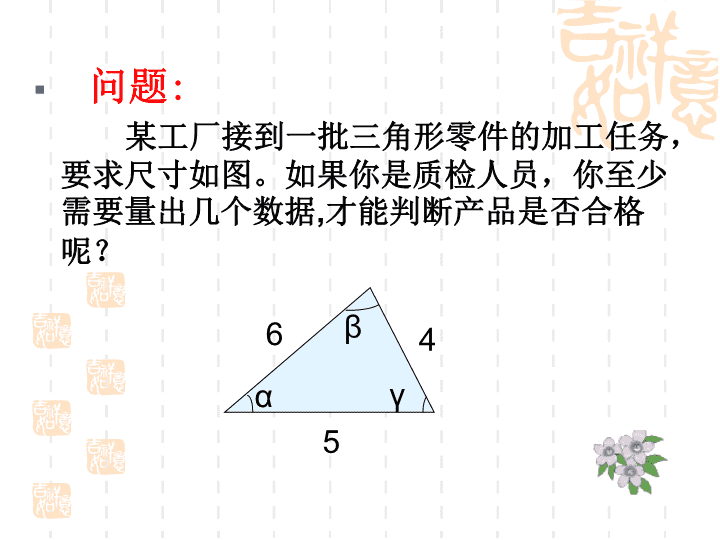
第四章 三角形 4.3.3 探索三角形全等的条件 知识回顾 1 、什么是全等三角形？ 2 、 如图，△ ABC≌ △ DCB ，如果 AB=4㎝ ， ∠ ABC=70 ° ，∠ ACB=30 ° 则 DC= ， ∠ DCB= ， 　∠ DBC= 。　 　　　　　 4㎝ 70 ° 30 ° 问题 : 　　　 某工厂接到一批三角形零件的加工任务，要求尺寸如图。如果你是质检人员，你至少需要量出几个数据 , 才能判断产品是否合格呢？ 6 4 5 β γ α １、 当两个三角形只有一组边相等或一组角相等时，它们全等吗？ 　 2 、两个三角形中， （ 1 ）有两组边分别相等，它们全等吗？ 　 （ 2 ）有两组角分别相等，它们全等吗？ （ 3 ）有一组边、一组角分别相等，它们全等吗？ 　 （两组边相等） ３、 再增加一个条件有哪几种情况？ 　 （ 1 ）、两边一角； （ 2 ）、两角一边； （ 3 ）、边边边； （ 4 ）、角角角 这节课我们将研究第一种情况：两边一角 ? 两组边和一组角分别相等的两个三角形全等吗 ? 活动一 探索之路 　　 每人用一张长方形纸剪一个直角 三角形，怎样才能使全班同学剪下的直角 三角形都全等呢？ 2.5 E F D 3 60 º 探索之路 　　观察下面四个三角形，先猜一猜，再量一量，哪两个三角形是全等三角形？ 活动二 2.5 ① ② 3 H 45 º J ④ A B 45 º 3 2.5 C I M N P 45 º 3 2.5 ③ N M P 3 2.5 45º M N P 3 2.5 45º 2.5 E F D 3 60 º 探索之路 　　观察下面四个三角形，先猜一猜，再量一量，哪两个三角形是全等三角形？ 活动二 2.5 ① ② 3 H 45 º J ④ A B 45 º 3 2.5 C I M N P 45 º 3 2.5 ③ 1 、画∠ MAN=50 O ； 2 、在 AM 上截取 AB=8cm ；在 AN 上截取 AC=6cm ； 3 、连接 BC 。 剪下所得的△ ABC ，与周围同学所剪的比较一下，它们全等吗？ B C N A M 50 O ′ 画两边长分别为 6cm ， 8cm 并且它们的夹角为 50° 的三角形。 　两边和它们的夹角对应相等的两个三角形全等．简写成“边角边”或“ＳＡＳ” 结论： A B C D E F 在△ ABC 和△ DEF 中 , 因为 :AB=DE, ∠ABC=∠DEF, BC=EF 根据” SAS”, 所以 , △ABC≌△DEF 4 4 练一练 : 如图 , 在下列三角形中 , 哪两个三角形全等 ? 4 4 5 5 30° 30° 4 4 30° 4 6 40° 4 6 40° 40° ① ③ ② ⑥ ⑤ ④ 例题： 如图， AB=AD ，∠ BAC=∠DAC ，请问： △ ABC 和 △ ADC 是否全等？为什么？ D A B C 练习巩固 AB DC ≌ 在△ ABO 和△ DCO 中，若 AO=DO ，只要再有 = ， △ ABO ≌ △DCO 如果∠ ACB=∠DBC ，只要再有 = 　　　　　 也能说明△ ABC≌△DCB AC DB BO CO 生活中的数学 “ 五一”节期间 , 几名学生在公园，测量一池塘两端Ａ，Ｂ的距离，设计了如下方案：如图，先在平地上取了一个可直接到达Ａ，Ｂ的点Ｃ，再连接ＡＣ，ＢＣ，并分别延长ＡＣ至Ｄ，ＢＣ至Ｅ，使ＤＣ＝ＡＣ，ＥＣ＝ＢＣ，最后测ＤＥ的长即为ＡＢ的距离，你认为这种方案可行吗 ? 并加以说明 . A E B C D 练习巩固 通过这节课的学习你有什么收获 ? 本节课你学习了什么？ 发现了什么？ 有什么收获？ 还存在什么没有解决的问题？