七年级数学下册7-2平面直角坐标系课件新人教版

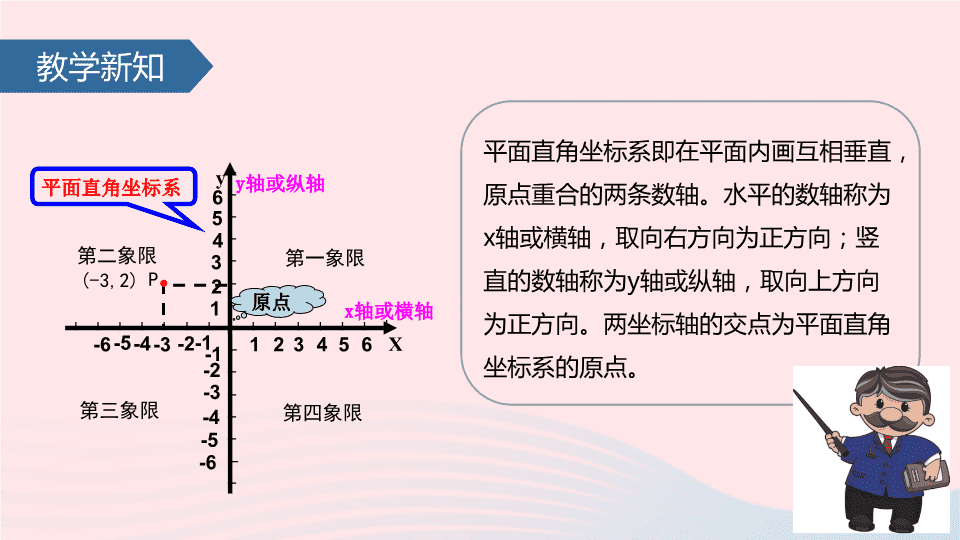
七年级数学下册7-2平面直角坐标系课件新人教版

第七章平面直角坐标系7.1.2平面直角坐标系y5-5-2-4-1231-664-55-3-44-23-121-66X-3x轴或横轴y轴或纵轴第一象限第二象限第三象限第四象限P(-3,2) 教学新知平面直角坐标系即在平面内画互相垂直，原点重合的两条数轴。水平的数轴称为x轴或横轴，取向右方向为正方向；竖直的数轴称为y轴或纵轴，取向上方向为正方向。两坐标轴的交点为平面直角坐标系的原点。y5-5-2-4-1231-664-55-3-44-23-121-66X-3x轴或横轴y轴或纵轴平面直角坐标系第一象限第二象限第三象限第四象限P(-3,2)原点 知识要点2.在给定的平面直角坐标系中，能由点的位置写出它的坐标，并会根据坐标描出点的位置，理解坐标平面内的点与有序实数对的一一对应关系。1.能正确地画出平面直角坐标系。 知识梳理知识点1：平面直角坐标系及点的坐标1.平面直角坐标系即在平面内画互相垂直，原点重合的两条数轴.水平的数轴称为x轴或横轴，取向右方向为正方向；竖直的数轴称为y轴或纵轴，取向上方向为正方向.两坐标轴的交点为平面直角坐标系的原点.2.建立平面直角坐标系后，坐标平面被两条坐标轴分成了四个部分，每个部分称为象限，分别叫做第一象限、第二象限、第三象限、第四象限，坐标轴上的点不属于任何象限. 知识梳理3.描出点的方法：先在x轴上找出表示横坐标的点，再在y轴上找出表示纵坐标的点，过这两个点分别作x轴和y轴的垂线，垂线的交点就是该点.注意：表示点的坐标时，必须横坐标在前，纵坐标在后，中间用逗号隔开.【例】如图7-1-22，在平面直角坐标系中：（1）描出下列各点：A（-2,3）,B（-1,-4）,C（4,3）,D（0,3）;（2）写出平面直角坐标系中E、F、G、H、M、N点的坐标. 知识梳理图7-1-22图7-1-23【讲解】（1）根据平面直角坐标系与点的坐标的特征，第一个数表示横坐标，第二个数表示纵坐标，然后找出各点即可得到图7-1-23；（2）根据平面直角坐标系写出各点的坐标，即E（2，0）、F（0，-4）、G（-2，2）、H（1，-2）、M（4，1）、N（-3，-2）． 知识梳理【方法小结】在平面直角坐标系中确定点的位置的方法：先在x轴上找出表示横坐标的点，再在y轴上找出表示纵坐标的点，过这两个点分别作x轴和y轴的垂线，垂线的交点就是该点.写点的坐标的方法正好相反，但要注意：横坐标在前，纵坐标在后，中间用逗号隔开.【小练习】如图7-1-24，在平面直角坐标系中,描出以下各点：A（4，3），B（-2，3）,C（-3，-1）,D（2，-2）,E（0，-1）,F（-1，0），G（0，0）．并指出各点所在的象限或坐标轴. 知识梳理图7-1-24图7-1-25答案：解：如图7-1-25，点A在第一象限，点B在第二象限，点C在第三象限，点D在第四象限，点E在y轴上，点F在x轴上，点G在原点. 知识梳理2.如图7-1-26，写出坐标系中各点的坐标.图7-1-26答案：解：A（-3，1），B（0，1），C（1，-1），D（-2，0），E（2，0），F（-1，-2）． 知识梳理3.如图7-1-27所示，建立平面直角坐标系，使点B，C的坐标分别为（0，0），（4，0）．写出点A，D，E，F，G的坐标，并指出它们所在的象限.图7-1-27 知识梳理答案：解：如图7-1-28，A（-2，3）第二象限，D（6，1）第一象限，E（5，3）第一象限，F（3，2）第一象限，G（1，5）第一象限.知识点2：各个象限内和坐标轴上点的坐标的符号特点.图7-1-28 知识梳理 知识梳理【例1】指出下列各点所在象限或坐标轴.A(－1，－2.5)，B()，D(7，9)，E(－π，0)，F(0，【讲解】点A在第三象限；点B在第四象限；点C在第二象限；点D在第一象限；点E在x轴上；点F在y轴上；点G是坐标原点.【方法小结】判断某一点所在象限或坐标轴，主要看这一点的横、纵坐标的符号，根据各象限内点的符号特点，以及坐标轴上的点的坐标特点就可以知道这一点所在的象限或坐标轴. 知识梳理【例2】点M(a，b)为平面直角坐标系中的点.(1)当a＞0，b＜0时，点M位于第几象限？(2)当ab＞0时，点M位于第几象限？(3)当a为任意实数，且b＜0时，点M位于第几象限？【讲解】(1)由a＞0，b＜0可知点M的横坐标符号为正，纵坐标符号为负，故可依各象限点的坐标的符号特征判定M点在第四象限.(2)∵ab＞0；则a＞0，b＞0，或a＜0，b＜0.∴点M在第一象限，或点M在第三象限.(3)∵a为任意实数，所以可取正数、零或负数，而b＜0，则说明纵坐标为负数.∴可判定有三种情况.即点M位于第四象限、第三象限或y轴的负半轴上. 知识梳理【方法小结】要判断点所在象限，需根据条件确定点横、纵坐标的符号，即a、b的符号.横、纵坐标的符号确定了这个点所在的象限或坐标轴.【小练习】1.指出下列各点的横坐标和纵坐标，并指出各点所在的象限．A（2，3）、B（-2，3）、C（-2，-3）、D（2，-3）答案：：A（2，3）横坐标是2，纵坐标是3，在第一象限；B（-2，3）横坐标是-2，纵坐标是3，在第二象限；C（-2，-3）横坐标是-2，纵坐标是-3，在第三象限；D（2，-3）横坐标是2，纵坐标是-3，在第四象限. 知识梳理2.下列各点A（-6，-3），B（5，2），C（-4，3.5），D(2，中考在线考点1：点的坐标.B和DAE和F【例1】（2015•金华）点P（4，3）所在的象限是（　　）.A.第一象限B.第二象限C.第三象限D.第四象限A 知识梳理【解析】因为点P（4，3）的横坐标是正数，纵坐标是正数，所以点P在平面直角坐标系的第一象限.故选：A．【方法小结】本题考查了点的坐标,解答本题的关键是掌握好四个象限的点的坐标的特征：第一象限正正,第二象限负正,第三象限负负,第四象限正负.【例2】（2015•柳州）如图7-1-29，点A（-2，1）到y轴的距离为（　　）.A.-2B．1C．2D．图7-1-29C 知识梳理图7-1-29【解析】根据点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度解答，即点A的坐标为（-2，1），则点A到y轴的距离为2．故选C．【方法小结】本题考查了点的坐标，熟记点到x轴的距离等于纵坐标的长度，到y轴的距离等于横坐标的长度是解题的关键. 知识梳理实战演练1.（2015•重庆）在平面直角坐标系中，若点P的坐标为（-3，2），则点P所在的象限是（　　）.A.第一象限B.第二象限C.第三象限D.第四象限2.（2015•广安）如果点M（3，x）在第一象限，则x的取值范围是___________.3.（2015•广元）若第二象限内的点P（x，y）满足|x|=3,y2=25，则点P的坐标是___________.Bx＞0（-3，5） 知识梳理考点2：规律型：点的坐标.【例3】（2015•河南）如图7-1-30所示，在平面直角坐标系中，半径均为1个单位长度的半圆O1、O2、O3，…组成一条平滑的曲线，点P从原点O出发，沿这条曲线向右运动，速度为每秒个单位长度，则第2015秒时，点P的坐标是（　　）A.（2014,0）B.（2015,-1）C.（2015,1）D.（2016,0）B 知识梳理图7-1-30【解析】半径为1个单位长度的半圆的周长为：个半圆，当点P从原点O出发，沿这条曲线向右运 知识梳理动,运动时间为1秒时,点P的坐标为（1,1）;当点P从原点O出发,沿这条曲线向右运动,运动时间为2秒时,点P的坐标为（2,0）;当点P从原点O出发,沿这条曲线向右运动,运动时间为3秒时，点P的坐标为（3，-1）；当点P从原点O出发，沿这条曲线向右运动，运动时间为4秒时，点P的坐标为（4，0）；当点P从原点O出发，沿这条曲线向右运动，运动时间为5秒时，点P的坐标为（5，1）；当点P从原点O出发，沿这条曲线向右运动，运动时间为6秒时，点P的坐标为（6，0）；…，∵2015÷4=503…3∴A2015的坐标是（2015，-1），故选：B.【方法小结】此题考查了点的规律变化，解答本题的关键是仔细观察图象，得到点的变化规律，解决问题. 知识梳理实战演练（2015•甘孜州）如图7-1-31，正方形A1A2A3A4，A5A6A7A8，A9A10A11A12，…，（每个正方形从第三象限的顶点开始，按顺时针方向顺序，依次记为A1，A2，A3，A4；A5，A6，A7，A8；A9，A10，A11，A12；…）的中心均在坐标原点O，各边均与x轴或y轴平行，若它们的边长依次是2，4，6…，则顶点A20的坐标为_____________.（5，-5） 知识梳理图7-1-31 课堂练习1.如图7-1-32所示，点A的坐标是().A．(3，2)B．(3，3)C．(3，-3) D．(-3，-3)图7-1-32B 课堂练习2.如图7-1-32所示，横坐标和纵坐标都是负数的点是().A．A点   B．B点C．C点   D．D点3.如图7-1-32所示，坐标是(-2，2)的点是().A．点A    B．点B   C．点C    D．点DCD4.点A(-3，2)在第_______象限，点D(3，-2)在第_______象限，点C(3，2)在第______象限，点D(-3，-2)在第_______象限，点E(0，2)在______轴上，点F(2，0)在______轴上.二四一三yx 课堂练习5.点A(-2，-1)与x轴的距离是________；与y轴的距离是________.6.点A(3，a)在x轴上,点B(b，4)在y轴上,则a=______，b=______.12007.已知：点P（2m+4，m-1）．试分别根据下列条件，求出P点的坐标．（1）点P在y轴上；（2）点P在x轴上；（3）点P的纵坐标比横坐标大3；（4）点P在过A（2，-3）点，且与x轴平行的直线上. 课堂练习答案：解：（1）令2m+4=0，解得m=-2，所以P点的坐标为（0，-3）；（2）令m-1=0，解得m=1，所以P点的坐标为（6，0）；（3）令m-1=（2m+4）+3，解得m=-8，所以P点的坐标为（-12，-9）；（4）令m-1=-3，解得m=-2．所以P点的坐标为（0，-3）．讲评：（1）让横坐标为0求得m的值，代入点P的坐标即可求解；（2）让纵坐标为0求得m的值，代入点P的坐标即可求解；（3）让纵坐标-横坐标=3得m的值，代入点P的坐标即可求解；（4）让纵坐标为-3求得m的值，代入点P的坐标即可求解. 课堂练习8.已知点A（1+2a，4a-5），且点A到两坐标轴的距离相等，求点A的坐标.答案：解：根据题意，分两种情况讨论：①1+2a=4a-5，解得：a=3∴1+2a=4a-5=7，∴点A的坐标为（7，7）；②1+2a+4a-5=0，解得：a=∴1+2a=，4a-5=-，∴点A的坐标为（讲评：本题考查了点的坐标.根据点A到两坐标轴的距离相等，分两种情况讨论：1+2a与4a-5相等；1+2a与4a-5互为相反数. 课堂练习9.已知四边形ABCD各顶点的坐标分别是A（0，0），B（1，2），C（7，4），D（8，0）（1）请建立平面直角坐标系，并画出四边形ABCD．（2）求四边形ABCD的面积.图7-1-33 课堂练习答案：解：（1）如图7-1-33所示；（2）四边形ABCD的面积= 课后习题1.在平面直角坐标系中，点A（2，-3）在第（　　）象限.A．一B．二C．三D．四2.在下列所给出坐标的点中，在第二象限的是（　　）.A.（2，3）B.（-2，3）C.（-2，-3）D.（2，-3）3.已知x轴上的点P到y轴的距离为3,则点P的坐标为（）.A.(3,0)B.(0,3)C.(0,3)或(0,-3)D.(3,0)或(-3,0)4.点P（m+3，m-1）在x轴上，则点P的坐标为（　　）.A.（0，-2）B.（2，0）C.（4，0）D.（0，-4）DBDC 课后习题5.已知点M(a，b)，当a＞0，b＞0时，M在第_______象限；当a____，b______时，M在第二象限；当a_____，b_______时，M在第四象限；当a＜0，b＜0时，M在第______象限.一＜0＞0三＞0＜06.在平面直角坐标系中描出下列各点，并将各点用线段依次连接起来：A（2，1）B（6，1）C（6，3）D（7，3）E（4，6）F（1，3） 课后习题答案：如图7-1-34.图7-1-34 课后习题7.点P到x轴的距离是2，到y轴的距离是3，且在y轴的左侧，则P点的坐标是___________________________.8.已知点P（x，y）在第四象限，且|x|=3，|y|=5，则点P的坐标是__________________.9.已知点A（4，3），AB∥y轴，且AB=3，则B点的坐标为____________________________.（-3，2）或（-3，-2）（3，-5）（4，0）或（4，6） 课后习题10.在直角坐标系xOy中，已知（-5，2+b）在x轴上，N（3-a，7+a）在y轴上，求b和ON的值.答案：解：∵（-5，2+b）在x轴上，∴2+b=0，解得b=-2；∵N（3-a，7+a）在y轴上，∴3-a=0，解得a=3，所以，点N（0，10），ON=10．11.已知四边形ABCD各顶点坐标分别为A（3，-2），B（3，2），C（-3，2），D（-3，-2）．（1）建立平面直角坐标系，并画出四边形ABCD．（2）求四边形ABCD的面积. 课后习题答案：解：（1）如图7-1-35所示：（2）由图象可知：四边形ABCD为长方形，∵A（3，-2），B（3，2），C（-3，2），D（-3，-2），∴AB=4,AD=6，∴四边形ABCD的面积为：4×6=24．图7-1-35 课后习题12.如图7-1-36，将边长为1的正三角形OAP沿x轴正方向连续翻转2015次，点P依次落在点P1，P2，P3，…P2015的位置，则点P2015的横坐标为_____________.图7-1-36（2014，0） 课后习题13.x取不同的值时，点P（x-1，x+1）的位置不同，讨论当点P在不同象限或不同坐标轴上时，x的取值范围；并说明点P不可能在哪一个象限.答案：解：（1）当x=-1时，点P在x轴的负半轴上；（2）当x=1时，点P在y轴的正半轴上；（3）当x＞1时，点P在第一象限；（4）当-1＜x＜1时，点P在第二象限；（5）当x＜-1时，点P在第三象限；（6）点P不可能在第四象限.