七年级下数学课件：5-3-1 平行线的性质 （共17张PPT）2_人教新课标

七年级下数学课件：5-3-1 平行线的性质 （共17张PPT）2_人教新课标

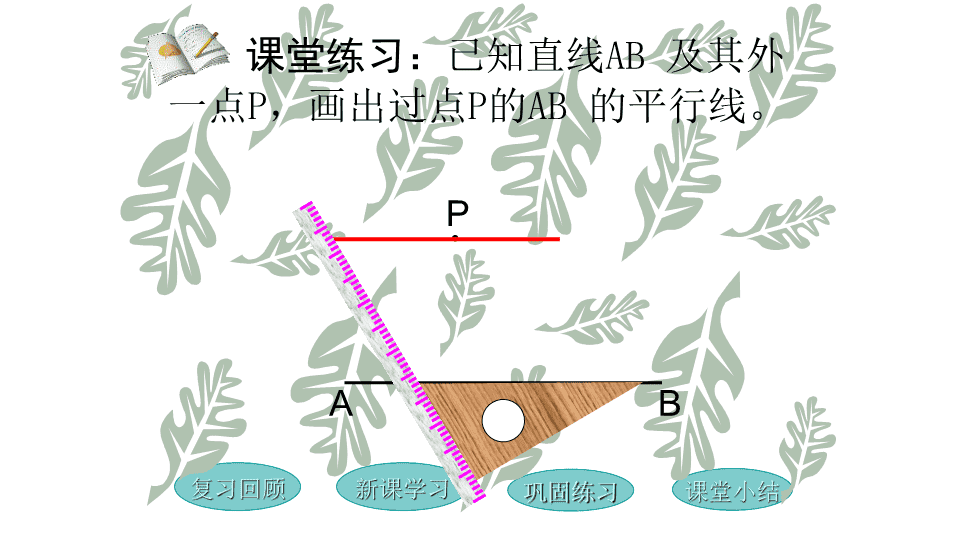
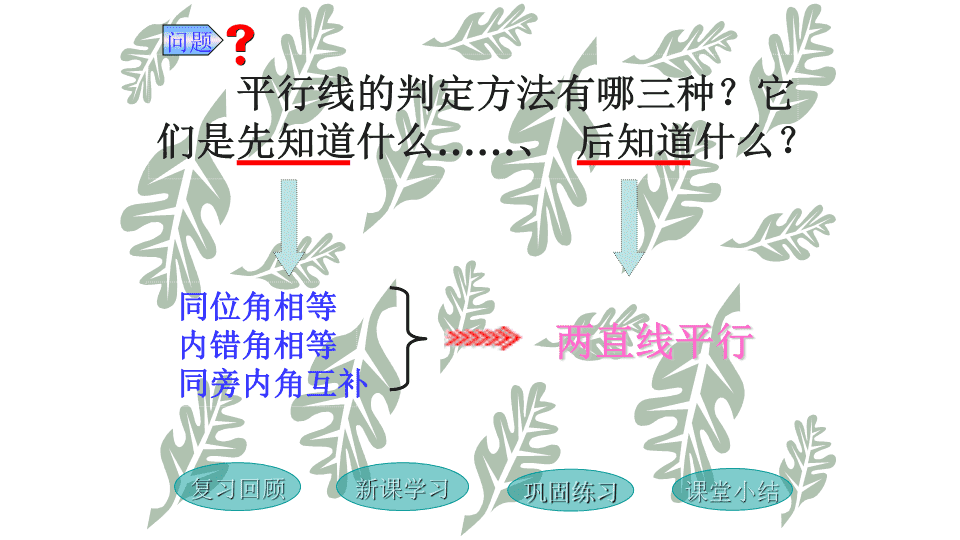
复习回顾新课学习巩固练习课堂小结平行线的性质 复习回顾新课学习巩固练习课堂小结ABP课堂练习：已知直线AB及其外一点P，画出过点P的AB的平行线。 平行线的判定方法有哪三种？它们是先知道什么……、后知道什么？同位角相等内错角相等同旁内角互补两直线平行问题复习回顾新课学习巩固练习课堂小结 如果两条直线平行，那么这两条平行线被第三条直线所截而成的同位角有什么数量关系？平行线的性质1（公理）两条平行线被第三条直线所截，同位角相等。简单说成：两直线平行，同位角相等。问题演示……结论性质2 ABPCDEF21复习回顾新课学习巩固练习课堂小结 ABCDEF21E’F’345687演示结论 a//b(已知）1=2（两直线平行，同位角相等）又1=3（对顶角相等）3=2（等量代换）123ab思考回答如图，已知：a//b那么3与2有什么关系？平行线的性质2两条平行线被第三条直线所截，内错角相等简单说成：两直线平行，内错角相等。结论复习回顾性质3巩固练习课堂小结 c231ba解：a//b（已知）1=2（两直线平行，同位角相等）1+3=180°（邻补角定义）2+3=180°（等量代换）如图：已知a//b，那么2与3有什么关系呢？平行线的性质3两条平行线被第三条直线所截，同旁内角互补简单说成：两直线平行，同旁内角互补。复习回顾性质1巩固练习课堂小结 平行线的性质1（公理）两条平行线被第三条直线所截，同位角相等。简单说成：两直线平行，同位角相等。平行线的性质2两条平行线被第三条直线所截，内错角相等简单说成：两直线平行，内错角相等。平行线的性质3两条平行线被第三条直线所截，同旁内角互补简单说成：两直线平行，同旁内角互补。精彩回放复习回顾新课学习巩固练习课堂小结 解：∵AD//BC（已知）∴A+B=180°（两直线平行，同旁内角互补）即B=180°-A=180°-115°=65°∵AD//BC（已知）∴D+C=180°（两直线平行，同旁内角互补）即C=180°-D=180°-100°=80°答：梯形的另外两个角分别为65°、80°。例1CBAD如图是梯形有上底的一部分。已经量得A=115°，D=100°，梯形另外两个角各是多少度？复习回顾新课学习巩固练习课堂小结 复习回顾新课学习巩固练习课堂小结CB解答：∵AB∥CD（已知）∴∠B=∠C(两直线平行，内错角相等)又∵∠B=142°∴∠B=∠C=142°（已知）（等量代换）ADP.86EX.1 4321ACBDE(1)∵AB∥CD（已知）∴∠1=∠2(两直线平行，内错角相等)又∵∠1=110°∴∠1=∠2=110°（已知）（等量代换）(2)∵AB∥CD（已知）∴∠1=∠3(两直线平行，同位角相等)又∵∠1=110°∴∠1=∠3=110°（已知）（等量代换）(3)∵AB∥CD（已知）∴∠1+∠4=180°(两直线平行，内错角相等)又∵∠1=110°（已知）∴110°+∠4=180°（等量代换）∴∠4=180°-110°=70°（等式性质）解答：P.86EX.2 平行线的“判定”与“性质”有什么不同比一比已知角之间的关系(相等或互补)，得到两直线平行的结论是平行线的判定。已知两直线平行，得到角之间的关系(相等或互补)的结论是平行线的性质。复习回顾新课学习巩固练习课堂小结 21DCBA如图：1=2（已知）AD//（）BCD+D=180（）BC内错角相等，两直线平行两直线平行，同旁内角互补填空：复习回顾新课学习巩固练习课堂小结 复习回顾新课学习巩固练习课堂小结EDCBA（已知）（1）∵∠ADE=60°∠B=60°∴∠ADE=∠B（等量代换）又∵∠ADE=∠B（已证）∴DE∥BC(同位角相等，两直线平行)（2）∵DE∥BC（已证）∴∠AED=∠C(两直线平行，同位角相等)又∵∠AED=40°（已知）（等量代换）∴∠C=40°解答：P.86EX.3 同位角相等内错角相等同旁内角互补两直线平行判定性质已知得到得到已知小结：复习回顾新课学习巩固练习课堂小结 复习回顾新课学习巩固练习课堂小结再见