七年级数学下册第二章相交线与平行线2探索直线平行的条件（第2课时）探索直线平行的条件（二）课件（新版）北师大版

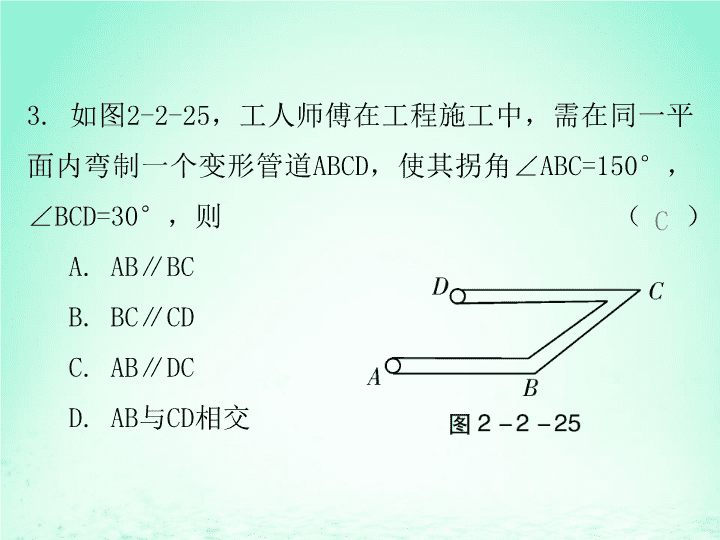
七年级数学下册第二章相交线与平行线2探索直线平行的条件（第2课时）探索直线平行的条件（二）课件（新版）北师大版

2探索直线平行的条件第二章相交线与平行线第2课时探索直线平行的条件（二） 课前预习1.同一平面内的四条直线若满足a⊥b，b⊥c，c⊥d，则下列式子成立的是（　）A.a∥dB.b⊥dC.a∥dD.a∥c2.如图2-2-24，下列条件，不能判断直线l1∥l2的是（　）A.∠1=∠3B.∠1=∠4C.∠2+∠3=180°D.∠3=∠5DA 3.如图2-2-25，工人师傅在工程施工中，需在同一平面内弯制一个变形管道ABCD，使其拐角∠ABC=150°，∠BCD=30°，则（　）A.AB∥BCB.BC∥CDC.AB∥DCD.AB与CD相交C 4.下列说法：①平面内过一点有且只有一条直线和已知直线垂直；②垂线段最短；③平行于同一条直线的两条直线也互相平行；④同位角相等.其中正确的个数有（　）A.1个B.2个C.3个D.4个C 课堂讲练新知1同旁内角互补，两直线平行典型例题【例1】如图2-2-26，BE平分∠ABD，DE平分∠BDC，且∠1+∠2=90°.求证：AB∥CD. 证明：因为BE平分∠ABD，DE平分∠BDC（已知），所以∠ABD=2∠1，∠BDC=2∠2（角平分线定义）.因为∠1+∠2=90°，所以∠ABD+∠BDC=2（∠1+∠2）=180°.所以AB∥CD（同旁内角互补，两直线平行）. 模拟演练1.如图2-2-27，∠1∶∠2∶∠3=2∶3∶4，∠AFE=60°，∠BDE=120°，写出图中平行的直线，并说明理由.解：EF∥BC，DE∥AB.理由如下:因为∠1∶∠2∶∠3=2∶3∶4，∠1+∠2+∠3=180°，所以∠1=40°，∠2=60°，∠3=80°.因为∠AFE=60°，∠BDE=120°，所以∠AFE=∠2，∠BDE+∠2=180°.所以EF∥BC，DE∥AB. 新知2平行的基本公理及推论典型例题【例2】如图2-2-28，∠BAE=∠AEC=∠ECD=120°.求证：AB∥CD. 解：如答图2-2-1,过点E作EF，使得∠AEF=60°.因为∠BAE=120°，∠AEF=60°，所以∠BAE+∠AEF=120°+60°=180°.所以AB∥EF.因为∠AEC=120°，所以∠FEC=60°.所以∠FEC+∠ECD=60°+120°=180°.所以EF∥CD.根据“平行于同一直线的两直线平行”，可得AB∥CD. 【例3】如图2-2-29，已知直线a，点B，点C.（1）过点B画直线a的平行线，能画几条？（2）过点C画直线a的平行线，它与过点B的平行线平行吗？ 解：（1）如答图2-2-2，过直线a外的一点B画直线a的平行线，有且只有一条直线与直线a平行.（2）过点C画直线a的平行线，它与过点B的平行线平行.理由如下：如答图2-2-2，因为b∥a，c∥a，所以c∥b. 模拟演练2.下列说法正确的有（）①在同一平面内，不相交的两条直线平行；②在同一平面内，若射线a与射线b没有交点，则a∥b；③若线段AB与CD没有交点，则AB∥CD；④若a∥b，b∥c，则a∥c.A.1个B.2个C.3个D.4个B 3.下面说法是否正确，并说明理由.（1）a,b,c是直线，且a∥b，b∥c，则a∥c.（2）a,b,c是直线，且a⊥b，b⊥c，则a⊥c.解：（1）正确.因为如果两条直线都与第三条直线平行，那么这两条直线也互相平行，所以a,b,c是直线，且a∥b，b∥c，则a∥c.（2）不正确.因为在同一平面内，垂直于同一条直线的两条直线互相平行，所以a,b,c是直线，且a⊥b，b⊥c，则a∥c. 课后作业夯实基础新知1同旁内角互补，两直线平行1.如图2-2-30，下面推理正确的是（　）A.因为∠A+∠D=180°，所以AD∥BCB.因为∠C+∠D=180°，所以AB∥CDC.因为∠A+∠C=180°，所以AB∥CDD.因为∠A+∠D=180°，所以AB∥CDD 2.如图2-3-31，∠1，∠2，…,∠8是两条直线a，b被直线c所截后形成的八个角，则能够判定直线a∥b的是（　）A.∠3+∠4=180°B.∠1+∠8=180°C.∠5+∠7=180°D.∠2+∠6=180°B 3.下列选项不能判定两直线平行的是（　）A.内错角相等，两直线平行B.同位角相等，两直线平行C.同旁内角相等，两直线平行D.同一平面内，垂直于同一条直线的两条直线平行C 4.如图2-2-32，直线a，b都与直线c相交，给出下列条件：①∠1=∠2；②∠3=∠6；③∠4+∠7=180°；④∠5+∠8=180°.其中能判断a∥b的条件是（　　）A.①③B.②④C.①③④D.①②③④D 新知2平行的基本公理及推论5.下列结论正确的是（　　）A.不相交的两条直线叫做平行线B.两条直线被第三条直线所截，同位角相等C.垂直于同一直线的两条直线互相平行D.平行于同一直线的两条直线互相平行D 6.下面说法正确的个数为（　　）①过直线外一点有一条直线与已知直线平行；②过一点有且只有一条直线与已知直线垂直；③两角之和为180°，这两个角一定邻补角；④同一平面内不平行的两条直线一定相交.A.1个B.2个C.3个D.4个7.已知：a∥b，b∥c，则a∥c.理由是________________________________.B平行于同一直线的两条直线平行 8.如图2-2-33，∠B=∠C，∠B+∠D=180°，那么BC平行DE吗？为什么？解：BC∥DE.理由：因为∠B=∠C，∠B+∠D=180°（已知），所以∠C+∠D=180°（等量代换）.所以BC∥DE（同旁内角互补，两直线平行）. 能力提升9.如图2-2-34，已知∠1=∠2，∠3+∠4=180°，求证：AB∥EF. 证明：因为∠1=∠2，所以AB∥CD.因为∠3+∠4=180°，所以CD∥EF.所以AB∥EF（平行于同一直线的两条直线平行）.