七年级下数学课件《探索平行线的性质》课件2_苏科版

七年级下数学课件《探索平行线的性质》课件2_苏科版

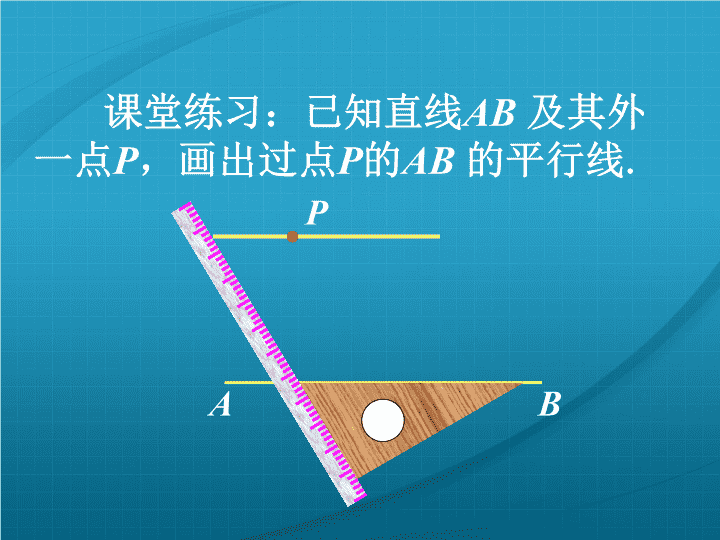
探索平行线的性质 ABP课堂练习：已知直线AB及其外一点P，画出过点P的AB的平行线. 问题：根据同位角相等可以判定两直线平行，反过来如果两直线平行同位角之间有什么关系呢？内错角，同旁内角之间又有什么关系呢？ 动手画一画！(1)用直尺和三角尺画出两条平行线a∥b，再画一条截线c，使之与直线a，b相交，并标出所形成的八角．(2)测量上面八个角的大小，记录下来．从中你能发现什么？ ABPCDEF问题如果两条直线平行，那么这两条平行线被第三条直线所截而成的同位角有什么数量关系？21 结论平行线的性质1两条平行线被第三条直线所截，同位角相等.简单说成：两直线平行，同位角相等. 123ab思考回答如图，已知：a//b那么3与2有什么关系？平行线的性质2两条平行线被第三条直线所截，内错角相等简单说成：两直线平行，内错角相等.例如：如右图因为a∥b，所以∠1=∠2()，又∠3=___(对顶角相等)，所以∠2=∠3.两直线平行，同位角相等∠1 c231ba如图：已知a//b，那么∠2与∠3有什么关系呢？平行线的性质3两条平行线被第三条直线所截，同旁内角互补简单说成：两直线平行，同旁内角互补.解：a//b（已知）∠1=∠2（两直线平行，同位角相等）∠1+∠3=180°（邻补角定义）∠2+∠3=180°（等量代换）∵∵∵∴ 性质1：两直线平行，同位角相等．性质2：两直线平行，内错角相等．性质3：两直线平行，同旁内角互补．平行线的性质： 例如图7-15，AB∥CD，∠A=∠D．判断AF与ED的位置关系，并说明理由．这样，由∠A=∠D、∠D=∠BED，可得∠A=∠BED.因为∠A=∠BED，所以AF∥ED.理由是：同位角相等，两直线平行．解：AF∥ED因为AB∥CD，所以∠D=∠BED.理由是：两直线平行，内错角相等． 练习如图，直线a∥b，∠1=54°，∠2，∠3，∠4各是多少度？解:∵∠2=∠1(对顶角相等)∴∠2=∠1=54°∵a∥b(已知)∴∠4=∠1=54°(两直线平行，同位角相等)∠2+∠3=180°(两直线平行，同旁内角互补)∴∠3=180°－∠2=180°－54°=126°1234ab EDCBA（已知）（1）∵∠ADE=60°∠B=60°∴∠ADE=∠B（等量代换）∴DE∥BC(同位角相等，两直线平行)（2）∵DE∥BC（已证）∴∠AED=∠C(两直线平行，同位角相等)又∵∠AED=40°（已知）（等量代换）∴∠C=40°已知∠ADE=60°，∠B=60°，∠AED=40°.证：（1）DE∥BC（2）∠C的度数 如图：∠1=∠2（已知）AD//（）∠BCD+∠D=180°（）BC内错角相等，两直线平行两直线平行，同旁内角互补∵21DCBA如图：已知∠1=∠2求证：∠BCD+∠D=180° 平行线的“判定”与“性质”有什么不同比一比 图形已知结果结论同位角内错角同旁内角两直线平行同旁内角互补122324））））））abababccc平行线的性质小结a//b两直线平行同位角相等a//b两直线平行内错角相等a//b