七年级下数学课件《多边形的内角和与外角和》 (3)_苏科版

七年级下数学课件《多边形的内角和与外角和》 (3)_苏科版

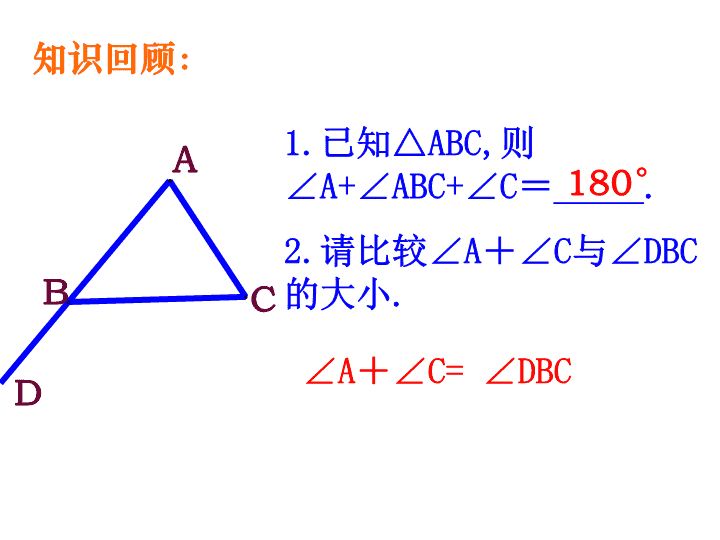
多边形的内角与外角和 ABC1.已知△ABC,则∠A+∠ABC+∠C＝_____.2.请比较∠A＋∠C与∠DBC的大小.D知识回顾：180°∠A＋∠C=∠DBC 探索多边形的内角和 美国国防部大楼——五角大楼看一看 看一看 了解一下在平面内，由不在同一条直线上的3条或3条以上的线段首尾依次相接组成的图形叫做多边形。顶点内角边对角线(连接不相邻两个顶点的线段) 我们现在研究的是如图1所示的多边形，是凸多边形；如图2所示的多边形，是凹多边形，但不在现在研究的范围中。今后如果不说明，我们讲的多边形都是凸多边形。图2比一比图1 看一看四边形五边形六边形八边形……任意一个四边形的内角和如何计算？五边形呢？六边形呢？...... 把四边形问题转化为熟悉的三角形问题来解决.归纳 DABC连接BD，把四边形ABCD分成2个三角形，将求四边形ABCD内角和的问题转化为求△ABD与△DCB的内角和。则四边形的内角和是_____四边形的内角和是多少？360° EABCD五边形的内角和是多少？五边形的内角和是_____0540 FABCDE六边形的内角和是多少？六边形的内角和是_____0720 DABCEABCDFABCDEn边形的内角和是多少？如图：四边形可以分成____个三角形，五边形可以分成____个三角形，六边形可以分成____个三角形n边形可以分成____个三角形234(n-2) DABCEABCDFABCDE多边形的边数34567…n分成三角形的个数123…多边形的内角和18001800×21800×3…45n-2180°×4180°×5180°×(n-2) 由此我们得出了：n边形的内角和等于（n-2)·1800你还有其他的方法计算多边形的内角和吗？ DABC四边形还可以这样分：那么四边形的内角和可以表示为：4×1800－3600 五边形还可以这样分：那么五边形的内角和可以表示为：5×1800－3600EABCD 六边形还可以这样分：那么六边形的内角和可以表示为：6×1800－3600FABCDE 多边形的边数4567…n分成三角形的个数45…多边形的内角和4×1800-36005×1800-3600…DABCEABCDFABCDE6×1800-36007×1800-3600n×1800-360067n 例题讲解：1.已知四边形的四个内角的度数的比为1：2：3：4，求这个四边形最大的角的度数.解：设每份为x,则四个角表示为x，2x，3x，4x，由题意得：x＋2x＋3x＋4x＝（4－2）×1800解得x=360最大的角为4×360＝1440 一个多边形的内角和为1080°，这个多边形是几边形？解：设这个多边形为n边形，由题意可得：180×（n-2）＝1080解得：n＝8答：这个多边形为8边形.练一练 练一练如图：四边形ABCD中，∠A与∠C互补，那么它的另一组对角∠B与∠D有什么关系？DCBA解：∠B与∠D互补。四边形ABCD中，∠A＋∠B＋∠C＋∠D＝3600∠A与∠C互补，即∠A＋∠C＝1800，所以∠B＋∠D＝3600－（∠A＋∠C）＝1800，即∠B与∠D互补。 想一想观察下图中的多边形，它们的边角有什么特点？在平面内，内角都相等、边也都相等的多边形叫做正多边形。 练一练1、如图：(1)作多边形所有过顶点A的对角线，并分别用字母表达出来。(2)求这个多边形的内角和。ABCDEF解：(1)过顶点A的对角线共有三条，分别是AC、AD和AE.(2)这个多边形的内角和是：(6-2)·1800=7200 练一练2、如果一个多边形的内角和是1440度，那么这是边形。解：由多边形的内角和公式可得（n-2）·1800=14400(n-2)=8n=10∴这是十边形。十 练一练3、若正n边形的一个内角是144度，那么n=.解：由多边形的内角和公式可得：(n-2)·180=144n180n–360=144n180n-144n=36036n=360n=1010 练一练4、在四边形ABCD中，∠A=120度，∠B：∠C：∠D=3：4：5，求∠B，∠C，∠D的度数。 有两个多边形，它们的边数之比1：2，内角和的度数之比为1：4，求这两个多边形的边数各是多少？多边形除去一个内角外，其余内角的和是11300，则这个多边形内角是多少度？这个多边形的边数是多少？练一练 如图：△ABC纸片沿DE折叠，使点A落在四边形BCDE的内部.∠A与∠1＋∠2之间存在怎样的数量关系？请试着找出来，并说明理由.21BCDEA解:2∠A＝∠1＋∠2在△ABC中，∠A＋∠B＋∠C＝1800①在△ADE中，∠A＋∠ADE＋∠AED＝1800②由①②，得∠B＋∠C＝∠ADE＋∠AED又在四边形BCDE中∠B＋∠C＋∠1＋∠2＋∠ADE＋∠AED＝3600，所以∠1＋∠2＋2（1800－∠A）＝3600，即2∠A＝∠1＋∠2 课堂小结谈谈你这节课的收获：（1）这节课我们主要学习了多边形的内角和公式。（2）从多边形的一个顶点出发可以引（n-3）条对角线，把多边形分成（n-2）个三角形。课堂作业：P345、6、7 教后记本节课中通过将多边形内角和转化成三角形的内角和,使学生比较容易掌握.运用内角和公式解题时也做得较好.