七年级下册数学课件《简单的轴对称性图形》 (1)_北师大版

七年级下册数学课件《简单的轴对称性图形》 (1)_北师大版

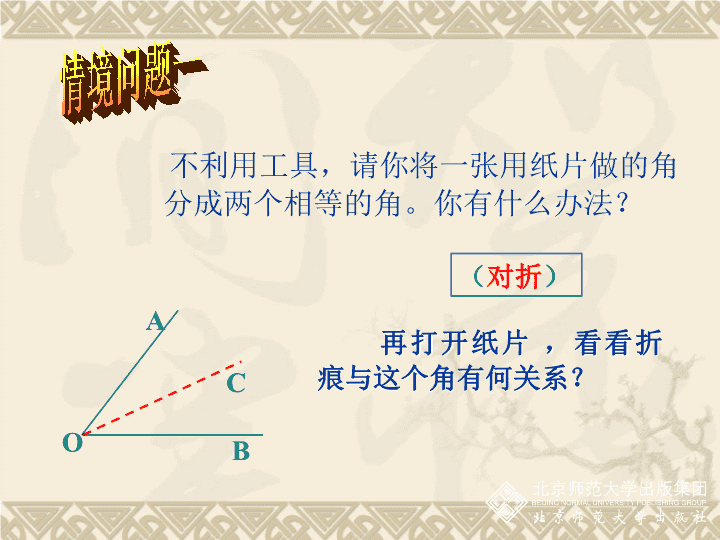
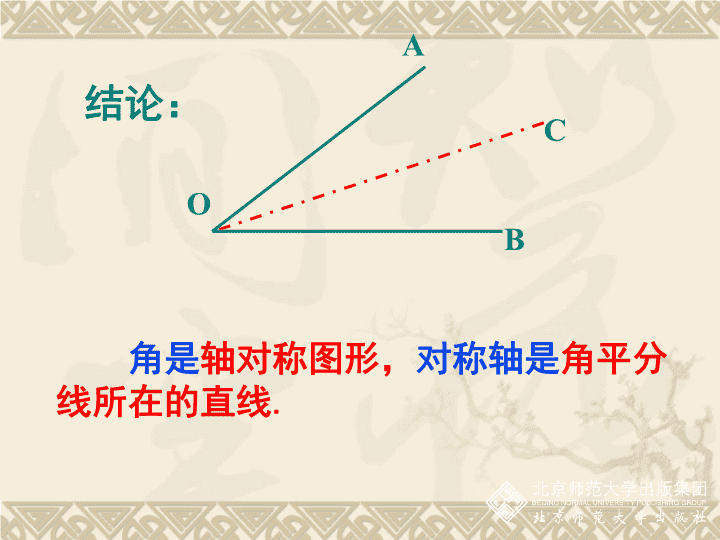
第五章生活中的轴对称3简单的轴对称图形（第3课时）ADCB 不利用工具，请你将一张用纸片做的角分成两个相等的角。你有什么办法？AOBC再打开纸片，看看折痕与这个角有何关系？（对折）情境问题一 C结论：角是轴对称图形，对称轴是角平分线所在的直线.ABO 有一个简易平分角的仪器（如图），其中AB=AD,BC=DC,将A点放在角的顶点，AB和AD与角的两边重合，沿AC画一条射线AE,AE就是∠BAD的平分线，为什么？对这种可以折叠的角可以用折叠方法得到角平分线，对不能折叠的角怎样得到其角平分线？情境问题二 根据角平分仪的制作原理怎样用尺规作一个角的平分线？NOMCE ２．分别以Ｍ，Ｎ为圆心．大于ＭＮ的长为半径作弧．两弧在∠AOB的内部交于Ｃ．用尺规作角的平分线的方法AＢＯＭＮＣ作法：１．以Ｏ为圆心，任意长为半径作弧，交ＯＡ于Ｍ，交ＯＢ于Ｎ．３．作射线OC．则射线ＯＣ即为所求． 将∠AOB对折，再折出一个直角三角形（使第一条折痕为斜边），然后展开，观察两次折叠形成的三条折痕，你能得出什么结论？情境问题三 (2)猜想:可以看一看,第一条折痕是∠AOB的平分线OC,第二次折叠形成的两条折痕PD,PE是角的平分线上一点到∠AOB两边的距离,这两个距离相等.角的平分线上的点到这个角的两边的距离相等。探究角平分线的性质 已知：如图，OC是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别是D，E。求证：PD=PE证明：DPEAOBC(3)验证猜想角的平分线上的点到角的两边的距离相等. 定理的作用：证明线段相等 （1）∵如图，AD平分∠BAC（已知）∴=，()在角的平分线上的点到这个角的两边的距离相等。BDCD（×）判断： （2）∵如图，DC⊥AC，DB⊥AB（已知）∴=，()在角的平分线上的点到这个角的两边的距离相等。BDCD（×） （3）∵AD平分∠BAC,DC⊥AC，DB⊥AB（已知）∴=，（）DBDC在角的平分线上的点到这个角的两边的距离相等。√ 1、如图，∵OC是∠AOB的平分线，又________________∴PD=PE()PD⊥OA，PE⊥OBBOACDPE角的平分线上的点到角的两边的距离相等练一练 2、在Rt△ABC中，BD是角平分线，DE⊥AB，垂足为E，DE与DC相等吗？为什么？ABCDE 3、已知△ABC中,∠C=900,AD平分∠CAB,且BC=8,BD=5,求点D到AB的距离是多少？ABCDE你会吗？思考： ◆这节课我们学习了哪些知识？1、角是轴对称图形，对称轴是角平分线所在的直线2、“作已知角的平分线”的尺规作图法；3、角的平分线的性质：111角的平分线上的点到角的两边的距离相等。∵OC是∠AOB的平分线,又PD⊥OA,PE⊥OB∴PD=PE(角的平分线上的点到角的两边距离相等).EDOABPC几何语言:小结拓展回味无穷1、 谢谢 证明：在△ACD和△ACB中AD=AB（已知）DC=BC（已知）CA=CA（公共边）∴△ACD≌△ACB（SSS）∴∠CAD=∠CAB（全等三角形的对应边相等）∴AC平分∠DAB（角平分线的定义）ADBCE 根据角平分仪的制作原理怎样用尺规作一个角的平分线？（不用角平分仪或量角器）NOMCE 已知：如图，OC是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别是D，E。求证：PD=PE证明：∵PD⊥OA，PE⊥OB（已知）∴∠PDO=∠PEO=90（垂直的定义）在△PDO和△PEO中∴PD=PE（全等三角形的对应边相等）∠PDO=∠PEO∠AOC=∠BOCOP=OP∴△PDO≌△PEO（AAS）DPEAOBC(3)验证猜想角的平分线上的点到角的两边的距离相等. 角平分线上的点到角两边的距离相等。(4)得到角平分线的性质：利用此性质怎样书写推理过程? 定理：角的平分线上的点到角的两边的距离相等用符号语言表示为：AOBPED12∵∠1=∠2PD⊥OA，PE⊥OB∴PD=PE(角的平分线上的点到角的两边的距离相等)推理的理由有三个，必须写完全，不能少了任何一个。 角平分线的性质角的平分线上的点到角的两边的距离相等。BADOPEC定理应用所具备的条件：（1）角的平分线；（2）点在该平分线上；（3）垂直距离。定理的作用：证明线段相等。 OABCEDP辨一辨如图，OC平分∠AOB，PD与PE相等吗？ 3、如图,OC是∠AOB的平分线,点P在OC上,PD⊥OA,PE⊥OB,垂足分别是D、E,PD=4cm,则PE=__________cm.ADOBEPC4