- 2021-10-21 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019七年级数学下册 第5章 相交线与平行线 5同位角、内错角、同旁内角
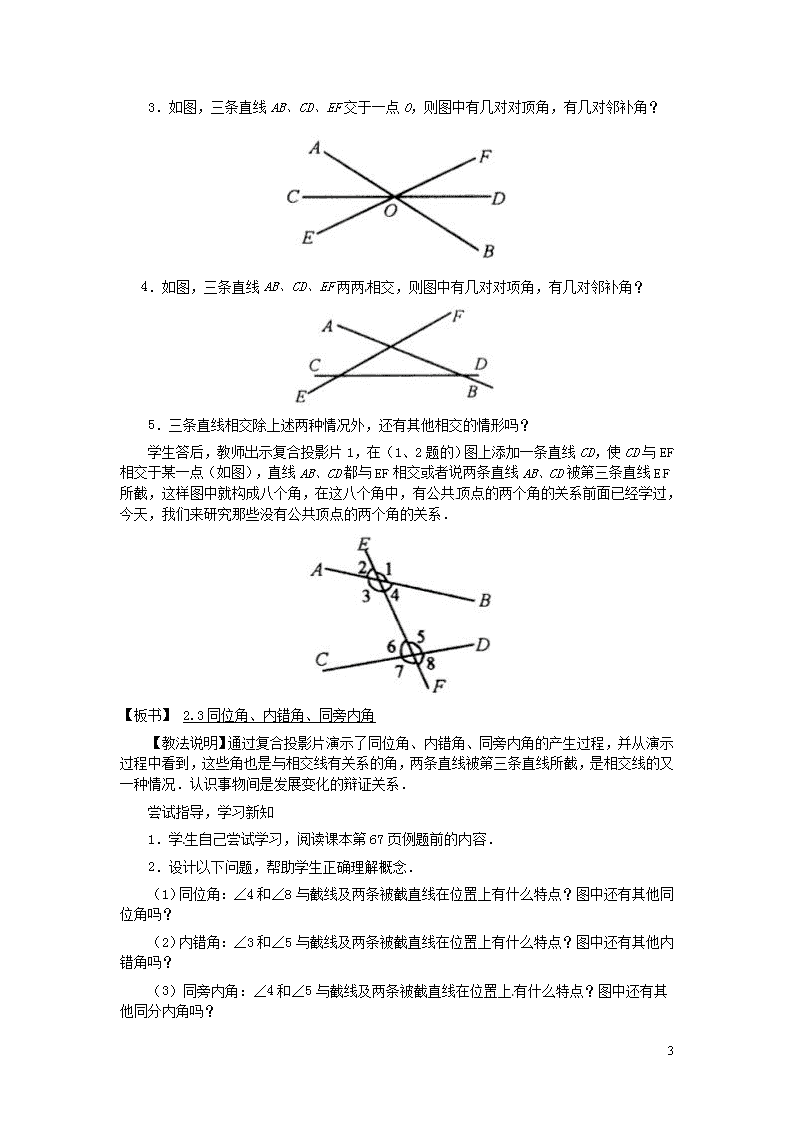
5 . 1.3 同位角、内错角、同旁内角 教学建议 一、知识结构 二、重点难点分析 本节教学的重点是同位角、内错角、同旁内角的概念.难点为在较复杂的图形中辨认同位角、内错角、同旁内角.掌握同位角、内错角、同旁内角的相关概念是进一步学习平行线、四边形等后续知识的基础. (1)两条直线被第三条直线所截,构成八个角(简称“三线八角”),其中同位角4对,内错角2对,同旁内角2对. (2)准确识别同位角、内错角、同旁内角的关键,是弄清哪两条直线被哪一条线所截.也就是说,在辨别这些角之前,要弄清哪一条直线是截线,哪两条直线是被截线. (3)在截线的同旁找同位角和同旁内角,在截线的两旁找内错角.要结合图形,熟记同位角、内错角、同旁内角的位置特点,比较它们的区别与联系. (4)在复杂的图形中识别同位角、内错角、同旁内角时,应当沿着角的边将图形补全,或者把多余的线暂时略去,找到三线八角的基本图形,进而确定这两个角的位置关系. 三、教法建议 1.上节课讨论了两条直线相交以后所形成的四个角,这一节课是进一步讨论三条直线相交后所形成的八个角,所以在教课过程,要运用基本图形结构将所学的知识及其内在联系向学生展示. 2.在讲三线八角概念时,一定要细致地分析、顾名思义,把握住两个关键的环节,“三条线与一条线”,尽量给出变式的图形,让学生分辨清楚. 3.这节课虽然不涉及两条直线平行后被第三条直线所截的问题,但在可能的情况下,将平行线的图形让学生见到,对下一步的学习很有好处,例如,平行四形中的内错角,学生开始接受起来有一定困难,在这一课时中,出现这个基本图形,为以后学习打下基础. 教学设计示例 一、素质教育目标 (一)知识教学点 1.理解同位角、内错角、同旁内角的概念. 2.结合图形识别同位角、内错角、同旁内角. (二)能力训练点 1.通过变式图形的识图训练,培养学生的识图能力. 2.通过例题口答“为什么”,培养学生的推理能力. (三)德育渗透点 6 从复杂图形分解为基本图形的过程中,渗透化繁为简,化难为易的化归思想;从图形变化过程中,培养学生辩证唯物主义观点. (四)美育渗透点 通过“三线八角”基本图形,使学生认识几何图形的位置美. 二、学法引导 1.教师教法:尝试指导,讨论评价、变式练习、回授. 2.学生学法:主动思考,相互研讨,自我归纳. 三、重点、难点、疑点及解决办法 (一)重点:同位角、内错角、同旁内角的概念. (二)难点:在较复杂的图形中辨认同位角、内错角、同旁内角. (三)疑点:正确理解新概念. (四)解决办法:引导学生讨论归纳三类角的特征,并以练习加以巩固. 四、课时安排:1课时 一、教具学具准备:投影仪、三角板、自制胶片. 六、师生互动活动设计 1.通过一组练习创设情境,复习基础知识,引入新课. 2.通过学生阅读书本,教师设问引导,练习巩固讲授新课. 3.通过师生互答完成课堂小结. 七、教学步骤 (一)明确目标 使学生掌握“三线八角”,并能在图形中进行辨识. (二)整体感知 以复习旧知创设情境引入课题,以指导阅读、设计问题、小组讨论学习新知,以变式练习巩固新知. (三)教学过程 创设情境,复习导入 回答下列问题: 1.如图,∠1与∠3,∠2与∠4是什么角?它们的大小有什么关系? 2.如图,∠1与∠2,∠l与∠4是什么角?它们有什么关系? 6 3.如图,三条直线AB、CD、EF交于一点O,则图中有几对对顶角,有几对邻补角? 4.如图,三条直线AB、CD、EF两两相交,则图中有几对对项角,有几对邻补角? 5.三条直线相交除上述两种情况外,还有其他相交的情形吗? 学生答后,教师出示复合投影片1,在(1、2题的)图上添加一条直线CD,使CD与EF相交于某一点(如图),直线AB、CD都与EF相交或者说两条直线AB、CD被第三条直线EF所截,这样图中就构成八个角,在这八个角中,有公共顶点的两个角的关系前面已经学过,今天,我们来研究那些没有公共顶点的两个角的关系. 【板书】 2.3同位角、内错角、同旁内角 【教法说明】通过复合投影片演示了同位角、内错角、同旁内角的产生过程,并从演示过程中看到,这些角也是与相交线有关系的角,两条直线被第三条直线所截,是相交线的又一种情况.认识事物间是发展变化的辩证关系. 尝试指导,学习新知 1.学生自己尝试学习,阅读课本第67页例题前的内容. 2.设计以下问题,帮助学生正确理解概念. (1)同位角:∠4和∠8与截线及两条被截直线在位置上有什么特点?图中还有其他同位角吗? (2)内错角:∠3和∠5与截线及两条被截直线在位置上有什么特点?图中还有其他内错角吗? (3)同旁内角:∠4和∠5与截线及两条被截直线在位置上有什么特点?图中还有其他同分内角吗? 6 (4)同位角和同分内角在位置上有什么相同点和不同点? 内错角和同旁内角在位置上有什么相同点和不同点? (5)这三类角的共同特征是什么? 3.对上述问题以小组为单位展开讨论,然后学生间互相评议. 4.教师对学生讨论过程中所发表的意见进行评判,归纳总结. 在截线的同旁找同位角和同旁内角,在截线的不同旁找内错角,因此在“三线八角”的图形中的主线是截线,抓住了截线,再利用图形结构特征(F、Z、U)判断问题就迎刃而解. 【教法说明】让学生自己尝试学习,可以充分发挥学生的积极性、主动性和创造性,几个问题的设计目的是深化教学重点,使学生看书更具有针对性,避免盲目性.学生互相评价可以增加讨论的深度,教师最后评价可以统一学生的观点,学生在议议评评的过程中明理、增智,培养了能力. 投影显示(投影片2) 例题 如图,直线DE、BC被直线AB所截,(1)∠l与∠2,∠1与∠3,∠1与∠4各是什么关系的角? (2)如果∠1=∠4,那么∠1和∠2相等吗?∠1和∠3互补吗?为什么? 6 [教法说明]例题较简单,让学生口答,回答“为什么”只要求学生能用文字语言把主要根据说出来,讲明道理即可,不必太规范,等学习证明时再严格训练. 变式训练,巩固新知 投影显示(投影片3) 【教法说明】本题是对简单变式图形的训练,以培养学生的识图能力,第2题指明第三条直线是c,即a和b被c所截,如c和a被占所截,则结果截然不同,因此遇到题目先分清哪两条直线被哪一条直线所栽,这是解题的关键和前提. 投影显示(投影片4) 6 【教法说明】本组练习是由同位角、内错角和同旁内角找出构成它们的“三线”,或是由“三线八角”图形判断同位角、内错角、同旁内角.这两者都需要进行这样的三个步骤,一看角的顶点;二看角的边;三看角的方位.这“三看”又离不开主线——截线的确定,让学生知道:无论图形的位置怎样变动,图形多么复杂,都要以截线为主线(不变),去解决万变的图形,另外遇到较复杂的图形,也可以从分解图形入手,把复杂图形化为若干个基本图形.如第2题由已知条件结合所求部分,对各个小题分别分解图 6查看更多