- 2021-10-21 发布 |
- 37.5 KB |
- 20页

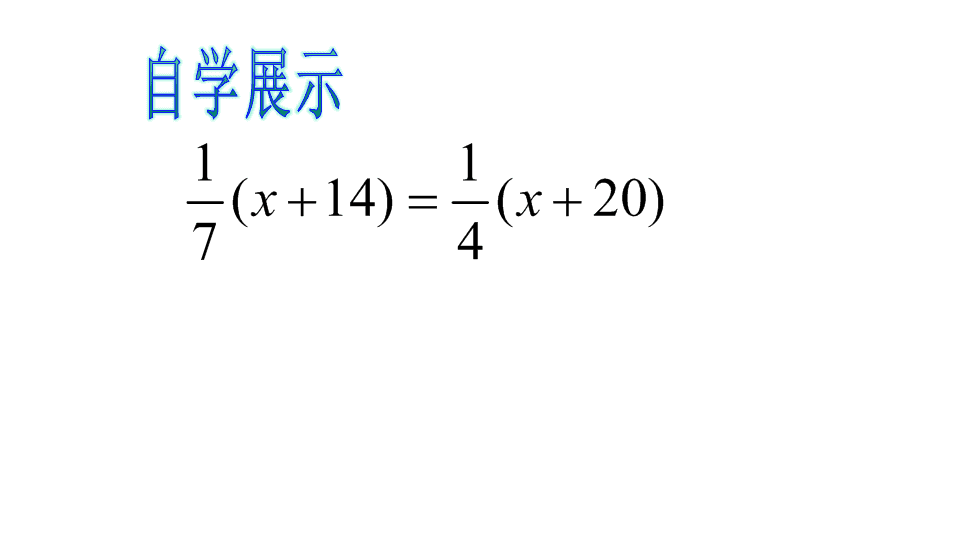

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级上数学课件- 3-3 解一元一次方程(二)——去分母 课件(共20张PPT)_人教新课标
)20(4 1)14(7 1 xx 还记得小学学习过的最小公倍数知识吗?回忆 一下,如何找出几个数的最小公倍数?求的最小 公倍数方法是什么? (1)4、6 (2)2、4、6 (3)2、6、9 短除法 3 4 2 3 xx 例1 解下列方程: 去分母得: 去分母得: 去分母得: 1. 将下列方程去分母。 (1) (2) (3) 4 3 2 1 xx 4 2 3 12 xx 2 22 7 13 xx 2(x-1)=x+3 4(2x-1)=3(2-x) 2(3x-1)=7(2+2x)14× ×14 4× ×4 12× ×12 例2 解下列方程: 16 2 3 yy 2. 将下列方程去分母。 (1) (2) 去分母得: 去分母得: 2 2 3 1 3 xxx 18 43 3 3 xx 2x-2(x-1)=3(2+x) 8(x-3)=3(3x-4)-24 24× ×24 ×24 6× ×6 ×6 注意: 最小公倍数 必须乘以方 程所有的项. )1(32 4223 13 xxx 1、小明是个“小马虎”下面是他做的题目,我们看看 对不对?如果 不对,请帮他改正。 (1)方程 04 1 2 xx 去分母,得 xx )1(263 11 xx 去分母,得 12 xx 3 1 6 12 2 xx 去分母,得 2123 xx 14 1 2 xx 去分母,得 8)1(24 xx 04 (2)方程 16 (4)方程 (3)方程 + √ ( ) 归纳总结: (2)用去分母解一元一次方程时应该注意哪些问题? (1)本节课学习了哪些主要内容? 解方程时要注意: ①去分母时各项同乘以所有分母的最小公倍数. ②去分母后分子是多项式时要加括号. ③去括号时要用乘法分配律,不要漏乘. 3 12 2 53 xx 解:整理得 归纳 解一元一次方程的一般步骤包括:去 分母、去括号、移项、合并同类项、系数 化为1等. 通过这些步骤可以使以x为未知 数的方程逐步向着x=a的形式转化,这个过 程主要依据等式的基本性质和运算律等. 练习2 某中学组织团员到校外参加义务植 树活动,一部分团员骑自行车先走,速度为 9 km/h,40分钟后其余团员乘汽车出发,速度为 45 km/h,结果他们同时到达目的地,则目的地 距学校多少千米? 解:设目的地距学校x km,则骑自行车所用时 间为 h,乘汽车所用时间为 h.9 x 45 x 由题意,得 解得 x=7.5.40 .9 45 60 x x- = 答:目的地距学校7.5 km. 1. 解方程 时,去分母正确的是( ) 112 3 x x A. 3x-1 = 2(x-1) B. 3x-6 = 2(x-1) C. 3x-6 = 2x-1 D. 3x-3 = 2x-1 B 2. 解方程: 2 11 5 2 x x 解:第一步________,得10 – 2(x + 2) = 5(x – 1). 第二步________,得10 –2x – 4 = 5x – 5. 第三步______,得 – 2x – 5x = –5 –10 + 4. 第四步____________,得 – 7x = –11. 第五步____________,得 x = . 去分母 去括号 移项 合并同类项 系数化为1 7 11 3. 列方程解答下面问题. y的3倍与1.5的和的二分 之一等于y与1的差的四分之一,求y. 解:根据题意,得 1 1(3 1.5) ( 1)2 4y y 解得 4 5y 4. 有一些相同的房间需要粉刷墙面,一天3名一 级技工去粉刷8个房间,结果其中有50 m2墙面未 来得及粉刷;同样时间内5名二级技工粉刷了10 个房间之外,还多粉刷了另外的40 m2墙面,每 名一级技工比二级技工一天多粉刷10 m2墙面, 求每个房间需要粉刷的墙面面积. 解:设每个房间需要粉刷的墙面面积为x m2. 解得 x = 52 答:每个房间需要粉刷的墙面面积为52 m2. 则 105 4010 3 508 xx 本课时的教学内容有关去分母解方程,与前 面去括号解方程相比,只是略微增加了一步,所 以本课时开头采用了引入旧知的方法帮助学生衔 接,接着以问题的形式进行师生互动,以帮助学 生真正掌握去分母解方程的方法.教学过程中, 教师要随时与学生保持互动,以了解学生的掌握 情况.此外,还应让学生多练习,以达到熟能生 巧的程度.查看更多