第4章第2节 种群数量的变化3

第4章第2节 种群数量的变化3

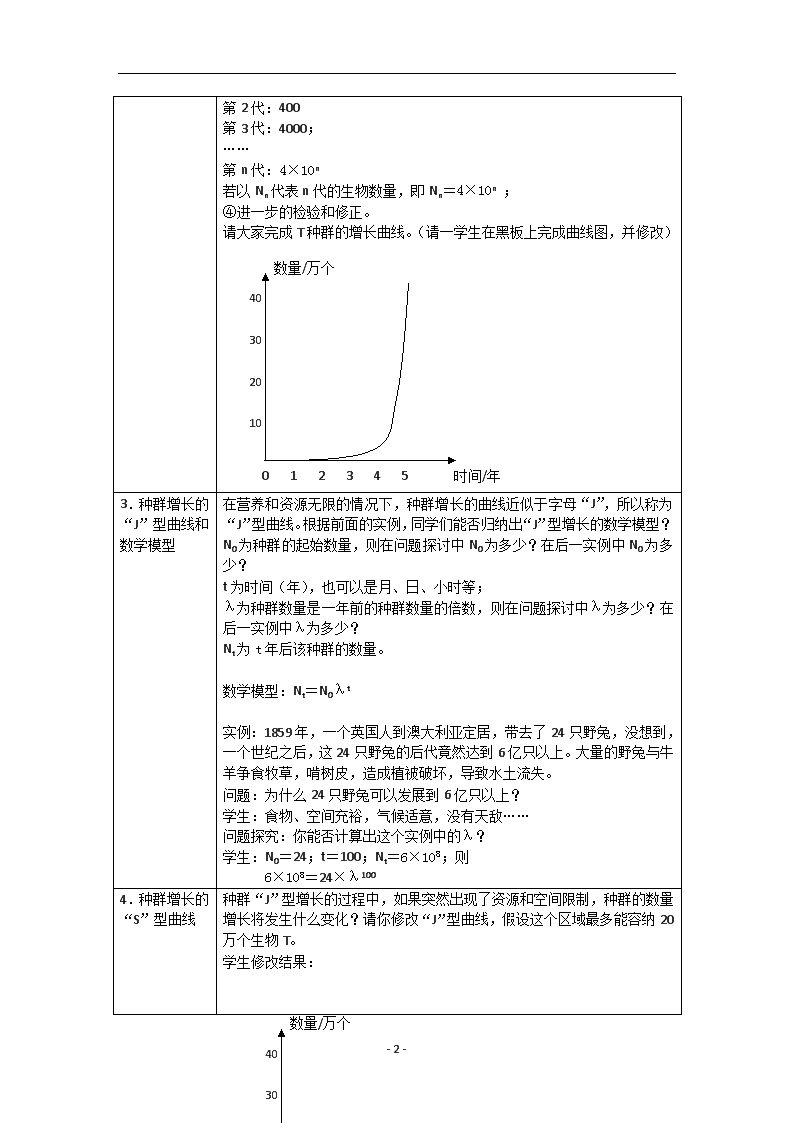
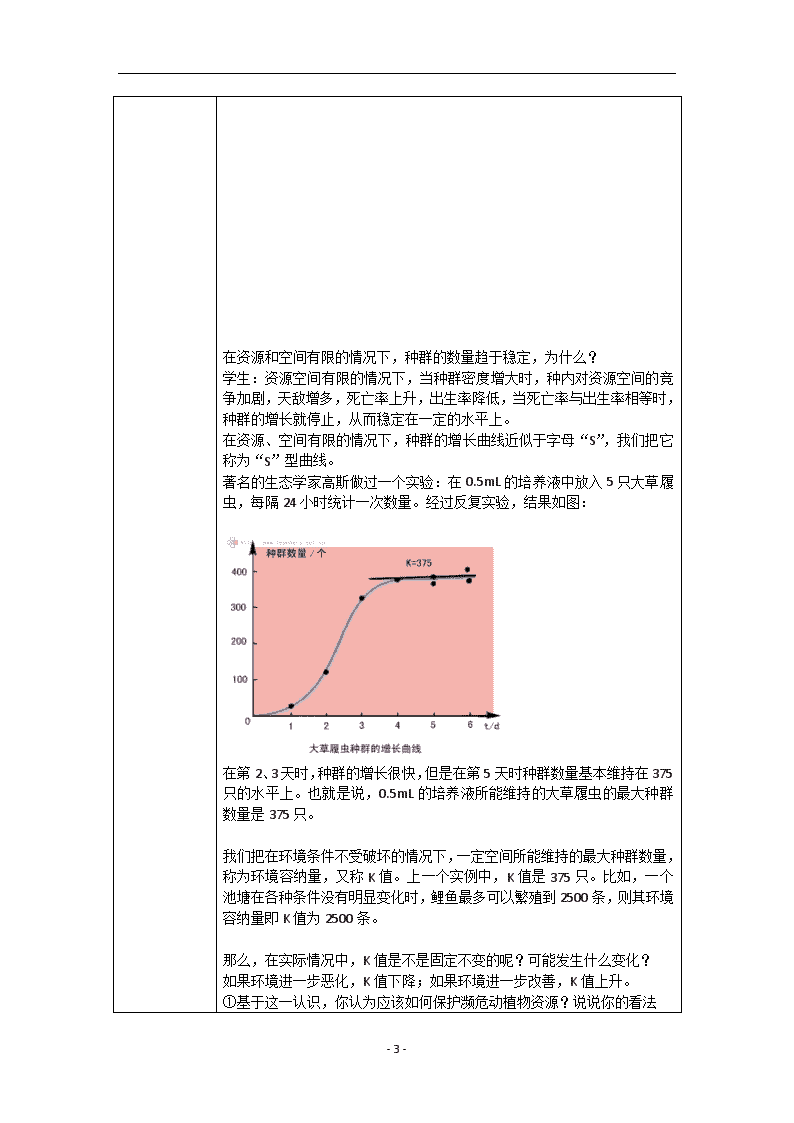
‎ ‎ 第4章　种群和群落 第2节 种群数量的变化 教学目标：说出构建种群增长数学模型的研究方法，尝试构建种群增长的数学模型；‎ ‎ 简述种群增长的变化；‎ 说出环境容纳量的含义；‎ ‎ 简述环境容纳量在保护濒危动植物的应用和在控制有害动物的应用 教学重点：尝试构建种群增长的数学模型 教学难点：尝试构建种群增长的数学模型 课时：1课时 教学过程设计：‎ 教学内容 教师行为与学生行为 ‎1．导入 教师以“问题讨论”直接引发学生讨论：在营养和生存空间无限的情况下，某种细菌每20min分裂一次。请同学们思考：n代细菌的数量是多少？（看教材 “细菌繁殖产生的后代数量”图）‎ 学生：2n 那么，你是怎么得到这个式子的？你是如何思考的？‎ ‎2．种群增长模型的构建 ‎（1）我们通过观察发现：‎ 观察对象，提出问题 细菌每20min分裂一次，分裂后 的数量是上一次的2倍 作出合理的假设 如果资源和空间无限的话，‎ 它的增长就不受种群密度的影响 第1代：2；‎ 根据实验数据，以数学形式描述事物的性质 第2代：4‎ 第3代：8；‎ ‎……‎ 第n代：2n ‎ 若以Nn代表n代的细菌数量，‎ 则可以数学形式表示：Nn＝2n 进一步观察和实验，检验和修正数学模型 数学模型是否正确，需要 ‎ 进一步的验证和修正。‎ ‎（2）接着，大家来尝试构建数学模型。‎ 在营养和生存空间无限的情况下，某种一年生生物T有4个体，一年后为40个个体。请同学们思考：此种生物第n年时的数量是多少？（要求同学们按照研究方法构建数学模型，临近同学可以讨论）‎ ‎①每隔一年繁殖一次，繁殖后的数量是前一年的10倍；‎ ‎②若资源和空间无限，其数量不受种群密度的影响；‎ ‎③第1代：40；‎ - 5 -‎ ‎ ‎ 第2代：400‎ 第3代：4000；‎ ‎……‎ 第n代：4×10n ‎ 若以Nn代表n代的生物数量，即Nn＝4×10n ；‎ ‎④进一步的检验和修正。‎ 请大家完成T种群的增长曲线。（请一学生在黑板上完成曲线图，并修改）‎ 数量/万个 时间/年 ‎0 1 2 3 4 5 ‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ ‎3．种群增长的“J”型曲线和数学模型 在营养和资源无限的情况下，种群增长的曲线近似于字母“J”，所以称为“J”型曲线。根据前面的实例，同学们能否归纳出“J”型增长的数学模型？‎ N0为种群的起始数量，则在问题探讨中N0为多少？在后一实例中N0为多少？‎ t为时间（年），也可以是月、日、小时等；‎ λ为种群数量是一年前的种群数量的倍数，则在问题探讨中λ为多少？在后一实例中λ为多少？‎ Nt为t年后该种群的数量。‎ 数学模型：Nt＝N0λt 实例：1859年，一个英国人到澳大利亚定居，带去了24只野兔，没想到，一个世纪之后，这24只野兔的后代竟然达到6亿只以上。大量的野兔与牛羊争食牧草，啃树皮，造成植被破坏，导致水土流失。‎ 问题：为什么24只野兔可以发展到6亿只以上？‎ 学生：食物、空间充裕，气候适意，没有天敌……‎ 问题探究：你能否计算出这个实例中的λ？‎ 学生：N0＝24；t＝100；Nt＝6×108；则 ‎ 6×108＝24×λ100‎ ‎4．种群增长的“S”型曲线 种群“J”型增长的过程中，如果突然出现了资源和空间限制，种群的数量增长将发生什么变化？请你修改“J”型曲线，假设这个区域最多能容纳20万个生物T。‎ 学生修改结果：‎ 数量/万个 时间/年 ‎0 1 2 3 4 5 ‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ - 5 -‎ ‎ ‎ 在资源和空间有限的情况下，种群的数量趋于稳定，为什么？‎ 学生：资源空间有限的情况下，当种群密度增大时，种内对资源空间的竞争加剧，天敌增多，死亡率上升，出生率降低，当死亡率与出生率相等时，种群的增长就停止，从而稳定在一定的水平上。‎ 在资源、空间有限的情况下，种群的增长曲线近似于字母“S”，我们把它称为“S”型曲线。‎ 著名的生态学家高斯做过一个实验：在0.5mL的培养液中放入5只大草履虫，每隔24小时统计一次数量。经过反复实验，结果如图：‎ 在第2、3天时，种群的增长很快，但是在第5天时种群数量基本维持在375只的水平上。也就是说，0.5mL的培养液所能维持的大草履虫的最大种群数量是375只。‎ 我们把在环境条件不受破坏的情况下，一定空间所能维持的最大种群数量，称为环境容纳量，又称K值。上一个实例中，K值是375只。比如，一个池塘在各种条件没有明显变化时，鲤鱼最多可以繁殖到2500条，则其环境容纳量即K值为2500条。‎ 那么，在实际情况中，K值是不是固定不变的呢？可能发生什么变化？‎ 如果环境进一步恶化，K值下降；如果环境进一步改善，K值上升。‎ ‎①基于这一认识，你认为应该如何保护濒危动植物资源？说说你的看法 - 5 -‎ ‎ ‎ 学生：建立自然保护区，改善栖息环境；‎ ‎ 禁止非法猎杀濒危动物和采集濒危植物；‎ ‎ 减少污染；‎ ‎ 避免人类活动的干扰。‎ ‎ 总之，目的是提高环境容纳量。‎ ‎②家鼠是有害动物之一，你认为应该用什么方法才能有效地控制家鼠的数量？‎ 学生：隐藏食物，避免暴露；‎ ‎ 堵塞洞穴，减少藏身之所；‎ ‎ 养猫；‎ ‎ 机械捕捉。‎ 总之，目的是降低环境容纳量。‎ ‎5．种群数量的波动和下降 可见，种群数量的变化受到了食物、空间、天敌、气候以及传染病等因素的影响。大多数的种群数量总是在波动之中的。鲸鱼的数量在二战时恢复到较高水平，但是战后捕鲸业恢复了，捕鲸船吨位不断上升，导致鲸的数量急剧下降，甚至濒临绝灭。图示日本捕鲸：日本在11月18日开始，在南太平洋海域进行一次大规模的捕鲸行动，他们挂着“科学研究”的旗号，不顾国际捕鲸协会的反对，坚决开始了日本迄今以来规模最大的一次捕鲸行动，并且计划捕鲸上千头，其中包括列入濒危物种的座头鲸。‎ 在了解这些资料以后，你认为我们应该如何合理地利用资源？从“S”型曲线来看，你认为应该在曲线的什么区域上利用资源最好？‎ 学生： K/2‎ 为什么？‎ 学生：增长速度最快，种群数量的恢复较快。‎ 如果在K/2之上呢？‎ 学生：可以，这时增长率降低了，但是种群数量较大，所以可以首先捕获一定数量的资源。‎ 如果在K/2之下呢?‎ 学生：不可以，增长率降低了，而且种群数量较小，很容易引起种群数量急剧减少，甚至濒临绝灭。‎ 数量/万个 时间/年 ‎0 1 2 3 4 5 ‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ 总而言之，我们要坚持合理的利用资源，以实现资源的可持续利用，避免资源由于过度利用而枯竭，这对于生态环境和人类社会的发展具有非常重要的意义。‎ 板书： 第二节 种群数量的变化 构建数学模型的方法 观察：20min分裂一次，2倍 假设：资源空间无限，增长不受影响 数学形式表达：第1次：2‎ 第2次：4‎ 第3次：8‎ - 5 -‎ ‎ ‎ ‎……‎ 第n次：2n Nn＝2n 检验修正 数量/万个 时间/年 ‎0 1 2 3 4 5 ‎ ‎40‎ ‎30‎ ‎20‎ ‎10‎ ‎“J”型曲线的数学模型：t表示时间（年），N0表示起始数量，‎ λ表示倍数，Nt表示t年后的种群数量。‎ 则 Nt＝N0×λt ‎ 条件：食物、空间充裕，气候适宜，没有天敌……‎ ‎“S”型曲线 条件：资源、空间有限 ‎ 环境容纳量：环境不受破坏，一定空间，最大数量（K值）‎ ‎ 环境恶化，K值降低；‎ ‎ 环境改善，K值升高。‎ 种群数量的波动和下降的因素：食物、空间、天敌、传染病、气候 对资源的利用：K/2，增长率最大，有利于资源的再生 教学反思：数学模型的建构体现了学科交叉的思想，在教学应适当给予渗透；另外，在教学内容最后最好能够做进一步的归纳和总结，使学生对本节课的内容有更清晰和概括的认识，并加强学生记忆。‎ - 5 -‎