2017届高考文科数学（全国通用）二轮适考素能特训：专题2-1-2向量、复数、算法、合情推理

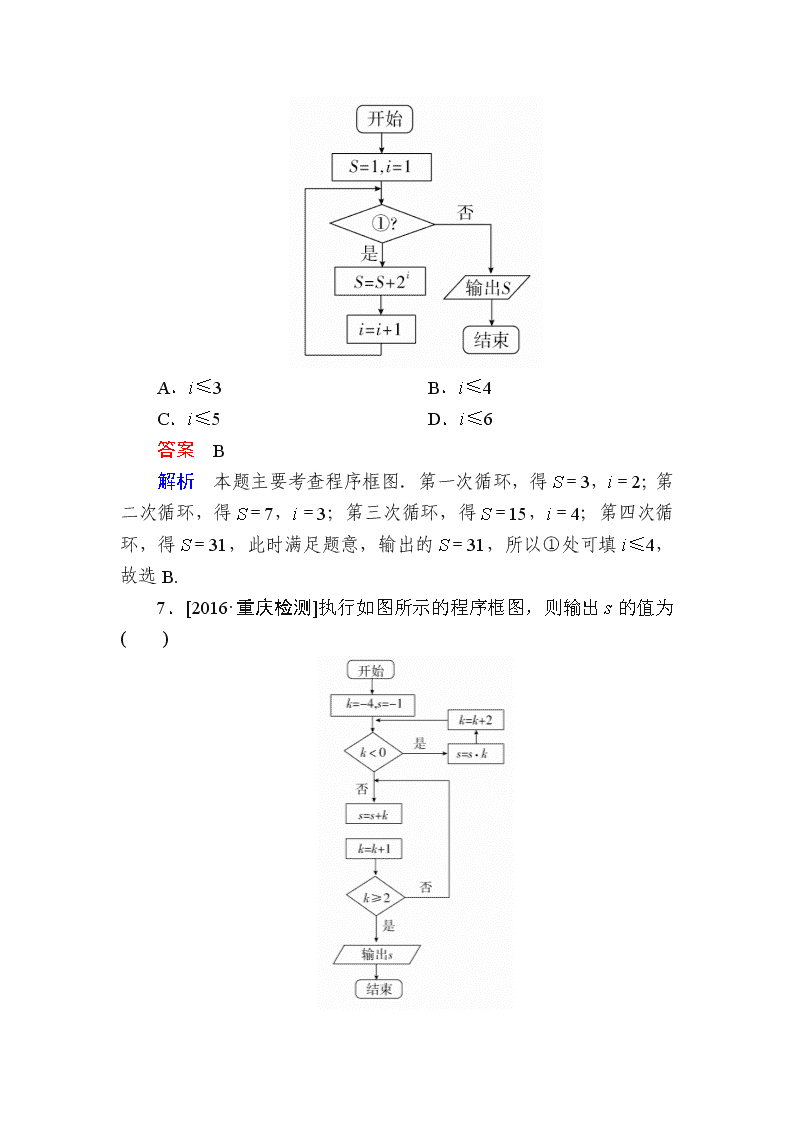
2017届高考文科数学（全国通用）二轮适考素能特训：专题2-1-2向量、复数、算法、合情推理

一、选择题 ‎1．[2016·沈阳质检]已知i为虚数单位，则复数在复平面内所对应的点在(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 答案　A 解析　本题主要考查复数的计算和复平面的概念.＝1＋i，其在复平面内对应的点为(1,1)，故选A.‎ ‎2．[2016·太原一模]已知复数z＝(i为虚数单位)，则z的虚部为(　　)‎ A．－1 B．0‎ C．1 D．i 答案　C 解析　z＝＝＝i，所以z的虚部是1.‎ ‎3．[2016·唐山统考]在等腰梯形ABCD中，＝－2，M为BC的中点，则(　　)‎ A.＋ B.＋ C.＋ D.＋ 答案　B 解析　本题主要考查平面向量的加减运算．因为＝－2，所以＝2.又M是BC的中点，所以＝(＋)＝(＋＋)＝( ‎＋＋)＝＋，故选B.‎ ‎4．[2016·沈阳质检]已知两个非零向量a，b满足a·(a－b)＝0，且2|a|＝|b|，则〈a，b〉＝(　　)‎ A．30° B．60°‎ C．120° D．150°‎ 答案　B 解析　本题主要考查平面向量数量积的运用．由题知a2＝a·b，而cos〈a，b〉＝＝＝，所以〈a，b〉＝60°，故选B.‎ ‎5．[2016·郑州质检]按如下程序框图，若输出结果为273，则判断框内应补充的条件为(　　)‎ A．i>7 B．i≥7‎ C．i>9 D．i≥9‎ 答案　B 解析　本题主要考查程序框图的应用．由程序框图可知：第一步，S＝0＋31＝3，i＝3；第二步，S＝3＋33＝30，i＝5；第三步，S＝30＋35＝273，i＝7.故判断框内可填i≥7，选B.‎ ‎6．[2016·贵阳质检]阅读如图所示的程序框图，为使输出的数据为31，则①处应填的表达式为(　　)‎ A．i≤3 B．i≤4‎ C．i≤5 D．i≤6‎ 答案　B 解析　本题主要考查程序框图．第一次循环，得S＝3，i＝2；第二次循环，得S＝7，i＝3；第三次循环，得S＝15，i＝4；第四次循环，得S＝31，此时满足题意，输出的S＝31，所以①处可填i≤4，故选B.‎ ‎7．[2016·重庆检测]执行如图所示的程序框图，则输出s的值为(　　)‎ A．－7 B．－5‎ C．2 D．9‎ 答案　A 解析　本题主要考查程序框图．依题意，执行题中的程序框图，k＝－4<0，s＝－1×(－4)＝4，k＝－4＋2＝－2；k＝－2<0，s＝4×(－2)＝－8，k＝－2＋2＝0；k＝0≥0，s＝－8＋0＝－8，k＝0＋1＝1；k＝1<2，s＝－8＋1＝－7，k＝1＋1＝2≥2，此时结束循环，输出s的值为－7，选A.‎ ‎8．在平面几何中有如下结论：正三角形ABC的内切圆面积为S1，外接圆面积为S2，则＝.推广到空间可以得到类似结论，已知正四面体P－ABC的内切球体积为V1，外接球体积为V2，则等于(　　)‎ A. B. C. D. 答案　C 解析　从平面图形类比空间图形，从二维类比三维，如图，设正四面体的棱长为a，E为等边三角形ABC的中心，O为内切球与外接球球心．‎ 则AE＝a，DE＝a，设OA＝R，OE＝r，‎ 则OA2＝AE2＋OE2，‎ 即R2＝2＋2，‎ ‎∴R＝a，r＝a，‎ ‎∴正四面体的外接球和内切球的半径之比为3∶1，故正四面体P－ABC的内切球体积V1与外接球体积V2之比等于.‎ ‎9．已知a，b是两个互相垂直的单位向量，且c·a＝c·b＝1，则对任意的正实数t，的最小值是(　　)‎ A．2 B．2 C．4 D．4 答案　B 解析　设a＝(1,0)，b＝(0,1)，则c＝(1,1)，‎ 代入得c＋ta＋b＝，‎ 所以＝ ‎＝≥2.‎ ‎10．[2016·广州模拟]已知△ABC的三个顶点A，B，C的坐标分别为(0,1)，(，0)，(0，－2)，O为坐标原点，动点P满足||＝1，则|＋＋|的最小值是(　　)‎ A.－1 B.－1‎ C.＋1 D.＋1‎ 答案　A 解析　本题主要考查向量的坐标运算，向量模的几何意义及坐标运算公式，圆的参数方程，三角函数的恒等变换．设P(cosθ，－2＋sinθ)，则|＋＋|＝＝＝≥ ＝－1.‎ 二、填空题 ‎11．如果z＝为纯虚数，则实数a等于________．‎ 答案　1‎ 解析　设z＝＝ti，则1－ai＝－t＋ti，，‎ a＝1.‎ ‎12．执行如图所示的程序框图，输出的S的值是________．‎ 答案　－1－ 解析　由程序框图可知，n＝1，S＝0；S＝cos，n＝2；S＝cos＋cos，n＝3；…；n＝2015，S＝cos＋cos＋cos＋…＋cos＝251cos＋cos＋…＋cos＋cos＋cos＋…＋cos＝251×0＋＋0＋＋(－1)＋ ‎＋0＝－1－，n＝2105，输出S.‎ ‎13．[2016·合肥质检]已知等边△ABC的边长为2，若＝3，＝，则·＝________.‎ 答案　－2‎ 解析　本题主要考查平面向量数量积的计算．如图所示，·＝(－)·(＋)＝·＝·＝2－2＝×4－×4＝－2.‎ ‎14. 如图所示，在平面上，用一条直线截正方形的一个角，截下的是一个直角三角形，有勾股定理c2＝a2＋b2.空间中的正方体，用一平面去截正方体的一角，截下的是一个三条侧棱两两垂直的三棱锥，若这三个两两垂直的侧面的面积分别为S1，S2，S3，截面面积为S，类比平面中的结论有________．‎ 答案　S2＝S＋S＋S 解析　建立从平面图形到空间图形的类比，在由平面几何的性质类比推理空间立体几何的性质时，注意平面几何中点的性质可类比推理空间几何中线的性质，平面几何中线的性质可类比推理空间几何中面的性质，平面几何中面的性质可类比推理空间几何中体的性质．所以三角形类比空间中的三棱锥，线段的长度类比图形的面积，于是作出猜想：S2＝S＋S＋S.‎