【数学】2018届一轮复习人教A版 二次函数与幂函数 学案
1.二次函数
(1)二次函数解析式的三种形式
①一般式f(x)=ax2+bx+c(a≠0).
②顶点式f(x)=a(x-m)2+n(a≠0).
③零点式f(x)=a(x-x1)(x-x2)(a≠0).
(2)二次函数的图像和性质
解析式
f(x)=ax2+bx+c(a>0)
f(x)=ax2+bx+c(a<0)
图像
定义域
(-∞,+∞)
(-∞,+∞)
值域
单调性
在x∈上单调递减;
在x∈上单调递增
在x∈上单调递增;
在x∈上单调递减
对称性
函数的图像关于x=-对称
2.幂函数
(1)定义形如y=xα(α∈R)的函数称为幂函数,其中x是自变量,α是常数.
(2)幂函数的图像比较
(3)幂函数的性质
①幂函数在(0,+∞)上都有定义;
②幂函数的图像过定点(1,1);
③当α>0时,幂函数的图像都过点(1,1)和(0,0),且在(0,+∞)上单调递增;
④当α<0时,幂函数的图像都过点(1,1),且在(0,+∞)上单调递减.
【思考辨析】
判断下面结论是否正确(请在括号中打“√”或“×”)
(1)二次函数y=ax2+bx+c,x∈[a,b]的最值一定是.( × )
(2)二次函数y=ax2+bx+c,x∈R,不可能是偶函数.( × )
(3)在y=ax2+bx+c(a≠0)中,a决定了图像的开口方向和在同一直角坐标系中的开口大小.( √ )
(4)函数y=2x是幂函数.( × )
(5)如果幂函数的图像与坐标轴相交,则交点一定是原点.( √ )
(6)当n<0时,幂函数y=xn是定义域上的减函数.( × )
1.已知a,b,c∈R,函数f(x)=ax2+bx+c.若f(0)=f(4)>f(1),则( )
A.a>0,4a+b=0 B.a<0,4a+b=0
C.a>0,2a+b=0 D.a<0,2a+b=0
答案 A
解析 因为f(0)=f(4)>f(1),所以函数图像应开口向上,即a>0,且其对称轴为x=2,即-=2,所以4a+b=0,故选A.
2.已知函数f(x)=ax2+x+5的图像在x轴上方,则a的取值范围是( )
A. B.
C. D.
答案 C
解析 由题意知即得a>.
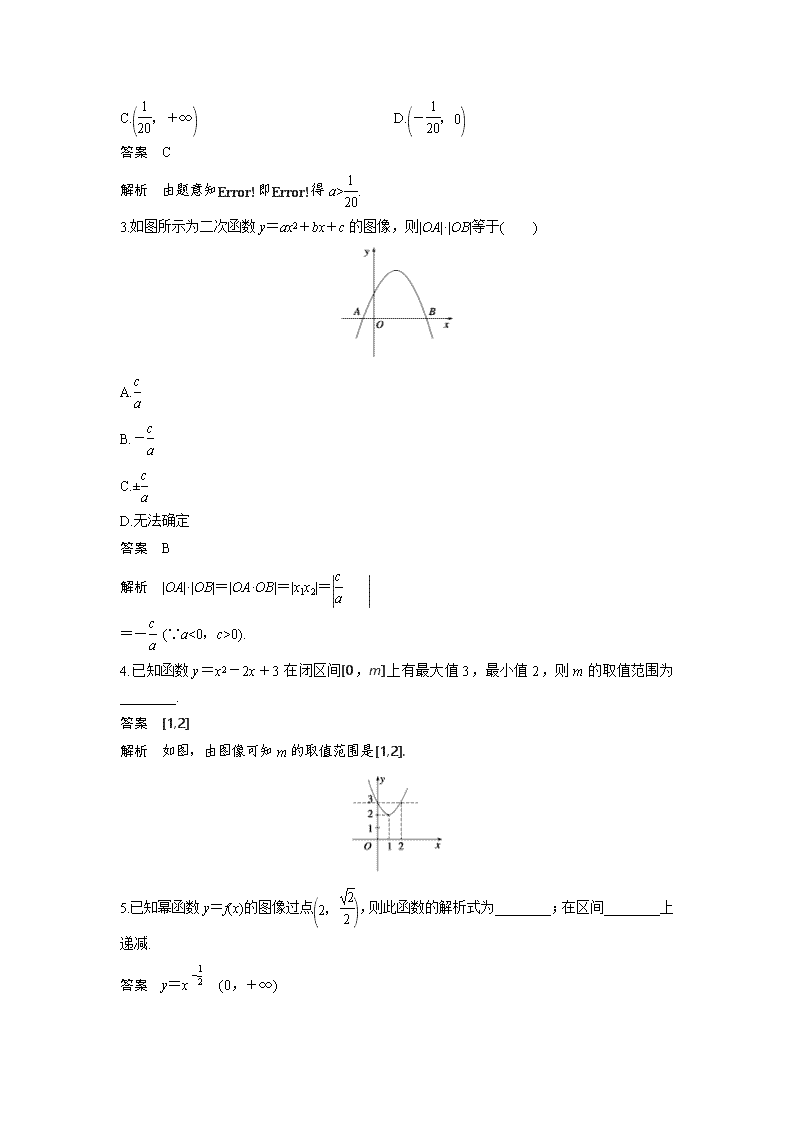
3.如图所示为二次函数y=ax2+bx+c的图像,则|OA|·|OB|等于( )
A.
B.-
C.±
D.无法确定
答案 B
解析 |OA|·|OB|=|OA·OB|=|x1x2|=
=- (∵a<0,c>0).
4.已知函数y=x2-2x+3在闭区间[0,m]上有最大值3,最小值2,则m的取值范围为________.
答案 [1,2]
解析 如图,由图像可知m的取值范围是[1,2].
5.已知幂函数y=f(x)的图像过点,则此函数的解析式为________;在区间________上递减.
答案 y=x (0,+∞)
题型一 求二次函数的解析式
例1 已知二次函数f(x)满足 f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定此二次函数的解析式.
解 方法一 (利用一般式)
设f(x)=ax2+bx+c(a≠0).
由题意得解得
∴所求二次函数为f(x)=-4x2+4x+7.
方法二 (利用顶点式)
设f(x)=a(x-m)2+n.∵f(2)=f(-1),
∴抛物线的图像的对称轴为x==.
∴m=.又根据题意函数有最大值8,∴n=8,
∴y=f(x)=a2+8.
∵f(2)=-1,
∴a2+8=-1,解得a=-4,
∴f(x)=-42+8=-4x2+4x+7.
方法三 (利用零点式)
由已知f(x)+1=0的两根为x1=2,x2=-1,
故可设f(x)+1=a(x-2)(x+1),
即f(x)=ax2-ax-2a-1.
又函数的最大值是8,即=8.
解得a=-4,
∴所求函数的解析式为f(x)=-4x2+4x+7.
(1)二次函数的图像过点(0,1),对称轴为x=2,最小值为-1,则它的解析式是___________________.
(2)若函数f(x)=(x+a)(bx+2a)(常数a,b∈R)是偶函数,且它的值域为(-∞,4],则该函数的解析式f(x)=________.
答案 (1)f(x)=x2-2x+1 (2)-2x2+4
解析 (1)依题意可设f(x)=a(x-2)2-1,
又其图像过点(0,1),
∴4a-1=1,∴a=.
∴f(x)=(x-2)2-1.
∴f(x)=x2-2x+1.
(2)由f(x)是偶函数知f(x)图像关于y轴对称,
∴b=-2,∴f(x)=-2x2+2a2,
又f(x)的值域为(-∞,4],
∴2a2=4,
故f(x)=-2x2+4.
题型二 二次函数的图像与性质
命题点1 二次函数的单调性
例2 已知函数f(x)=x2+2ax+3,x∈[-4,6],
(1)求实数a的取值范围,使y=f(x)在区间[-4,6]上是单调函数;
(2)当a=-1时,求f(|x|)的单调区间.
解 (1)函数f(x)=x2+2ax+3的图像的对称轴为x=-=-a,
∴要使f(x)在[-4,6]上为单调函数,只需-a≤-4或-a≥6,解得a≥4或a≤-6.
故a的取值范围是(-∞,-6]∪[4,+∞).
(2)当a=-1时,f(|x|)=x2-2|x|+3
=
其图像如图所示.
又∵x∈[-4,6],∴f(|x|)在区间[-4,-1)和[0,1)上为减函数,在区间[-1,0)和[1,6]上为增函数.
命题点2 二次函数的最值
例3 已知函数f(x)=x2-2x,若x∈[-2,3],则函数f(x)的最大值为________.
答案 8
解析 f(x)=(x-1)2-1,∵-2≤x≤3(如图),
∴[f(x)]max=f(-2)=8.
引申探究
已知函数f(x)=x2-2x,若x∈[-2,a],求f(x)的最小值.
解 ∵函数y=x2-2x=(x-1)2-1,
∴对称轴为直线x=1,
∵x=1不一定在区间[-2,a]内,∴应进行讨论,当-2
1时,函数在[-2,1]上单调递减,在[1,a]上单调递增,则当x=1时,y取得最小值,即ymin=-1.
综上,当-21时,ymin=-1.
命题点3 二次函数中的恒成立问题
例4 (1)(2015·石家庄模拟)设函数f(x)=ax2-2x+2,对于满足10,则实数a的取值范围为________.
(2)已知a是实数,函数f(x)=2ax2+2x-3在x∈[-1,1]上恒小于零,则实数a的取值范围为________.
答案 (1) (2)
解析 (1)由题意得a>-对1.
(2)2ax2+2x-3<0在[-1,1]上恒成立.
当x=0时,适合;
当x≠0时,a<2-,因为∈(-∞,-1]∪[1,+∞),当x=1时,右边取最小值,所以a<.
综上,实数a的取值范围是 .
思维升华 (1)二次函数最值问题解法抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合配方法,根据函数的单调性及分类讨论的思想即可完成.
(2)由不等式恒成立求参数取值范围的思路及关键
①一般有两个解题思路一是分离参数;二是不分离参数.
②两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否已分离.这两个思路的依据是a≥f(x)恒成立⇔a≥f(x)max,a≤f(x)恒成立⇔a≤f(x)min.
若二次函数f(x)=ax2+bx+c (a≠0),满足f(x+2)-f(x)=16x且f(0)=2.
(1)求函数f(x)的解析式;
(2)若存在x∈[1,2],使不等式f(x)>2x+m成立,求实数m的取值范围.
解 (1)由f(0)=2,得c=2,
所以f(x)=ax2+bx+2 (a≠0),
f(x+2)-f(x)=[a(x+2)2+b(x+2)+2]-[ax2+bx+2]=4ax+4a+2b.
因为f(x+2)-f(x)=16x,所以4ax+4a+2b=16x,
解得a=4,b=-8.
所以f(x)=4x2-8x+2.
(2)由f(x)>2x+m,
可得m(m2+m-1),则实数m的取值范围是( )
A. B.
C.(-1,2) D.
答案 (1)C (2)D
解析 (1)由幂函数的定义知k=1.又f=,
所以α=,解得α=,从而k+α=.
(2)因为函数y=x的定义域为[0,+∞),
且在定义域内为增函数,
所以不等式等价于
解2m+1≥0,得m≥-;
解m2+m-1≥0,得m≤或m≥.
解2m+1>m2+m-1,得-10时,f(x)=ax2-2x图像的开口方向向上,且对称轴为x=.[3分]
①当≤1,即a≥1时,f(x)=ax2-2x图像的对称轴在[0,1]内,
∴f(x)在[0,]上递减,在[,1]上递增.
∴f(x)min=f()=-=-.[6分]
②当>1,
即00),且f(m)<0,则( )
A.f(m+1)≥0 B.f(m+1)≤0
C.f(m+1)>0 D.f(m+1)<0
答案 C
解析 ∵f(x)的对称轴为x=-,f(0)=a>0,
∴f(x)的大致图像如图所示.
由f(m)<0,得-10,∴f(m+1)>f(0)>0.
4.若函数f(x)=x2-ax-a在区间[0,2]上的最大值为1,则实数a等于( )
A.-1 B.1
C.2 D.-2
答案 B
解析 ∵函数f(x)=x2-ax-a的图像为开口向上的抛物线,∴函数的最大值在区间的端点取得,
∵f(0)=-a,f(2)=4-3a,
∴或解得a=1.
5.幂函数y=x-1,y=xm与y=xn在第一象限内的图像如图所示,则m与n的取值情况为( )
A.-10,则一次函数y=ax+b为增函数,二次函数y=ax2+bx+c的开口向上,故可排除A;
若a<0,一次函数y=ax+b为减函数,二次函数y=ax2+bx+c开口向下,故可排除D;
对于选项B,看直线可知a>0,b>0,从而-<0,而二次函数的对称轴在y轴的右侧,故应排除B,因此选C.
7.当0g(x)>f(x)
解析 如图所示为函数f(x),g(x),h(x)在(0,1)上的图像,由此可知,h(x)>g(x)>f(x).
8.已知函数f(x)=x2-2ax+2a+4的定义域为R,值域为[1,+∞),则a的值为________.
答案 -1或3
解析 由于函数f(x)的值域为[1,+∞),
所以f(x)min=1.
又f(x)=(x-a)2-a2+2a+4,
当x∈R时,f(x)min=f(a)=-a2+2a+4=1,
即a2-2a-3=0,解得a=3或a=-1.
9.已知函数f(x)=ax2+bx+1(a,b为实数,a≠0,x∈R).
(1)若函数f(x)的图像过点(-2,1),且方程f(x)=0有且只有一个根,求f(x)的表达式;
(2)在(1)的条件下,当x∈[-1,2]时,g(x)=f(x)-kx是单调函数,求实数k的取值范围.
解 (1)因为f(-2)=1,即4a-2b+1=1,所以b=2a.
因为方程f(x)=0有且只有一个根,所以Δ=b2-4a=0.
所以4a2-4a=0,所以a=1,所以b=2.
所以f(x)=x2+2x+1.
(2)g(x)=f(x)-kx=x2+2x+1-kx=x2-(k-2)x+1=2+1-.
由g(x)的图像知要满足题意,则≥2或≤-1,即k≥6或k≤0,
所以所求实数k的取值范围为(-∞,0]∪[6,+∞).
10.已知函数f(x)=x2+ax+3-a,若x∈[-2,2]时,f(x)≥0恒成立,求a的取值范围.
解 要使f(x)≥0恒成立,则函数在区间[-2,2]上的最小值不小于0,设f(x)的最小值为g(a).
(1)当-<-2,即a>4时,g(a)=f(-2)=7-3a≥0,得a≤,故此时a不存在.
(2)当-∈[-2,2],即-4≤a≤4时,g(a)=f=3-a-≥0,得-6≤a≤2,又-4≤a≤4,
故-4≤a≤2.
(3)当->2,即a<-4时,g(a)=f(2)=7+a≥0,
得a≥-7,又a<-4,故-7≤a<-4,
综上得-7≤a≤2.
B组 专项能力提升
(时间20分钟)
11.已知函数f(x)=ax2+2ax+4(0f(x2)
D.f(x1)与f(x2)的大小不能确定
答案 B
解析 函数的对称轴为x=-1,
设x0=,由01时,恒有f(x)1时,恒有f(x)1时,函数f(x)=xα的图像在y=x的图像的下方,作出幂函数f(x)=xα在第一象限的图像,由图像可知α<1时满足题意.
13.已知a≤x2-3x+4≤b的解集为[a,b],则b=____,a+b的值为________.
答案 4 4
解析 设f(x)=x2-3x+4,则f(x)的最小值为1,因此a≤1(如果a>1,则a≤f(x)≤b的解集由两个区域构成),于是有f(a)=f(b)=b,而由f(b)=b,得b=4或,而函数y=f(x)图像的对称轴为x=2,故b=4,则f(a)=4,解得a=0(a=4舍去),所以a+b=4.
14.设0≤α≤π,不等式8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,则α的取值范围为_______.
答案 ∪
解析 由8x2-(8sin α)x+cos 2α≥0对x∈R恒成立,得Δ=(-8sin α)2-4×8cos 2α≤0,
即64sin2α-32(1-2sin2α)≤0,得到sin2α≤.
∵0≤α≤π,∴0≤sin α≤,
∴0≤α≤或≤α≤π.
即α的取值范围为∪.
15.已知函数f(x)=ax2+bx+c(a>0,b∈R,c∈R).
(1)若函数f(x)的最小值是f(-1)=0,且c=1,
F(x)=求F(2)+F(-2)的值;
(2)若a=1,c=0,且|f(x)|≤1在区间(0,1]上恒成立,试求b的取值范围.
解 (1)由已知c=1,a-b+c=0,且-=-1,
解得a=1,b=2,∴f(x)=(x+1)2.
∴F(x)=
∴F(2)+F(-2)=(2+1)2+[-(-2+1)2]=8.
(2)f(x)=x2+bx,原命题等价于-1≤x2+bx≤1在(0,1]上恒成立,
即b≤-x且b≥--x在(0,1]上恒成立.
又-x的最小值为0,--x的最大值为-2.
∴-2≤b≤0.故b的取值范围是[-2,0].