福建省泉州第十六中学2020届高三上学期期中考试数学（理）试题

福建省泉州第十六中学2020届高三上学期期中考试数学（理）试题

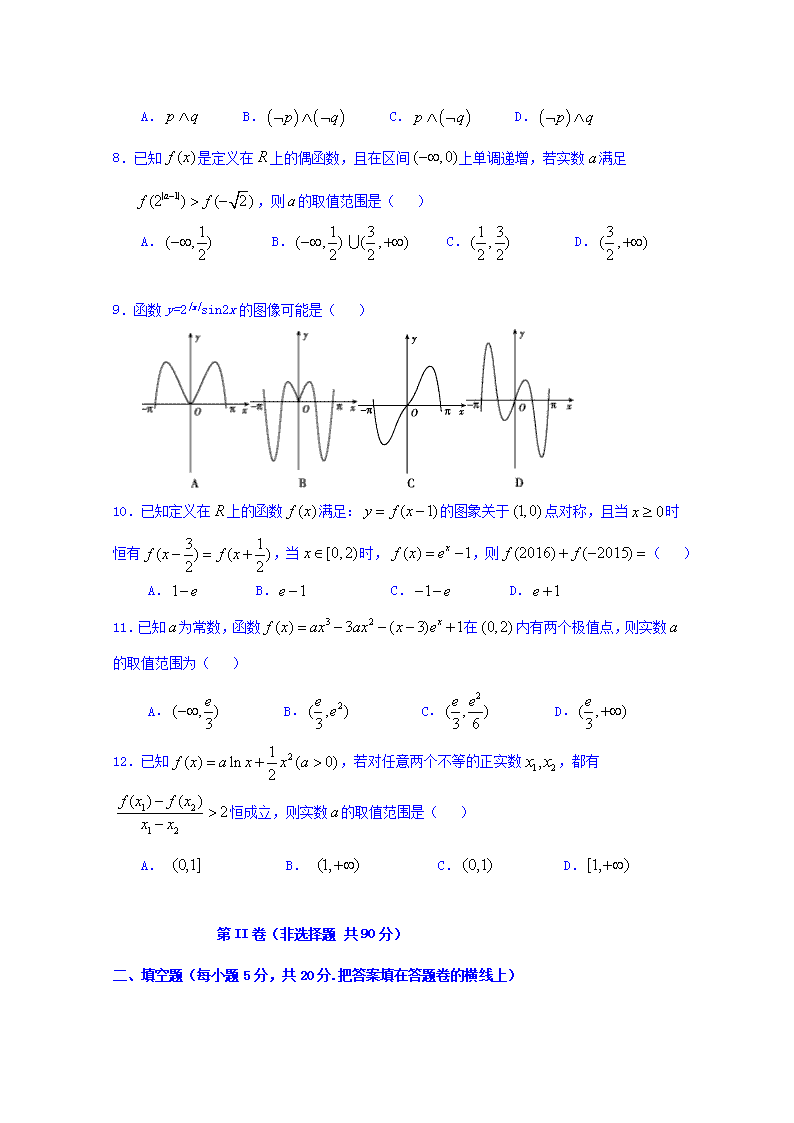
泉州第十六中学2019年秋季期中考试卷 高三数学（理科） ‎ 考试时间：120分钟 满分：150分 2019.11.8‎ 第I卷（选择题 共60分）‎ 一、选择题（本题共12小题，每小题5分，共60分，每题只有一个正确选项）‎ ‎1．设全集为R，集合，，则（ ）‎ A． B．‎ ‎ C． D．‎ ‎2．已知集合，则集合的子集个数为（ ）‎ A．1 B．‎2 C．3 D．4‎ ‎3．在中，为边上的中线，为的中点，则（ ）‎ A． B． ‎ C． D．‎ ‎4．已知向量与向量平行，则的值为（ ）‎ A． B． C． D．‎ ‎5．已知函数（)，下面结论错误的是（ )‎ A．函数的最小正周期为 B．函数是偶函数 C．函数的图象关于直线对称 D．函数在区间上是增函数 ‎6．△的内角，，所对的边分别为，，，已知，，，则（ ）‎ A． B．或 C．或 D．‎ ‎7．已知命题对任意，命题存在，使得，则下列命题为真命题的是（ ）‎ A． B． C． D．‎ ‎8．已知是定义在上的偶函数，且在区间上单调递增，若实数满足，则的取值范围是（ ）‎ A． B． C． D．‎ ‎9．函数y=2|x|sin2x的图像可能是（ ） ‎ ‎10．已知定义在上的函数满足：的图象关于点对称，且当时恒有，当时，，则（ ）‎ A． B． C． D．‎ ‎11．已知为常数，函数在内有两个极值点，则实数的取值范围为（ ）‎ A． B． C． D．‎ ‎12．已知，若对任意两个不等的正实数，都有恒成立，则实数的取值范围是（ ）‎ A． B． C． D．‎ 第II卷（非选择题 共90分）‎ 二、填空题（每小题5分，共20分.把答案填在答题卷的横线上）‎ ‎13．已知，若幂函数为奇函数，且在上单调递减，则α=_________‎ ‎14．已知曲线，则其在点处的切线方程是_______________‎ ‎15．在平面直角坐标系中，已知点A（-1，0），B（2，0），E，F是y轴上的两个动点，且||=2，则·的最小值为 __________．‎ ‎16．若函数在内有且只有一个零点，则在上的最大值与最小值的和为__________‎ 三、解答题：（本题共6个小题，共70分，解答应写出文字说明，证明过程和演算步骤）‎ ‎ 17．（本小题满分12分）设常数，函数 ‎（1）若为偶函数，求a的值；‎ ‎（2）若，求方程在区间上的解.‎ ‎18．（本小题满分12分）记分别为函数的导函数．若存在，满足且，则称为函数与的一个“S点”．‎ ‎（1）证明：函数与不存在“S点”；‎ ‎（2）若函数与存在“S点”，求实数a的值 ‎ 19．（本小题满分12分）在中，角所对的边分别为，，，且．‎ ‎（1）求角的值；‎ ‎（2）若为锐角三角形，且，求的取值范围．‎ ‎20. （本小题满分12分） 已知函数．‎ ‎（1）讨论的单调性；‎ ‎（2）若存在两个极值点，证明：．‎ ‎21．（本小题满分12分）某群体的人均通勤时间，是指单日内该群体中成员从居住地到工作地的平均用时，某地上班族S中的成员仅以自驾或公交方式通勤，分析显示：当S中的成员自驾时，自驾群体的人均通勤时间为 ‎（单位：分钟），‎ 而公交群体的人均通勤时间不受x影响，恒为40分钟，试根据上述分析结果回答下列问题：（1）当x在什么范围内时，公交群体的人均通勤时间少于自驾群体的人均通勤时间？‎ ‎（2）求该地上班族S的人均通勤时间的表达式；讨论的单调性，并说明其 实际意义.‎ ‎22.（本小题满分10分）选修4-4：坐标系与参数方程 在直角坐标系中，曲线的方程为.以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为.‎ ‎（1）求的直角坐标方程；‎ ‎（2）若与有且仅有三个公共点，求的方程.‎ 泉州第十六中学2019年秋季期中考试 ‎　高三数学（理科）试卷参考答案与评分标准 一、选择题（12小题，每题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D A C C B D C D A C D 二、填空题（4小题，每题5分，共20分）‎ ‎13． 14． 15． 16． ‎ 三、解答题：（本题共6个小题，共70分，解答应写出文字说明，证明过程和演算步骤）‎ ‎17.解：（1）=，‎ 当为偶函数时：，则，解得。‎ ‎（2），‎ 由题意，，‎ ‎，‎ 当时，即，‎ 令,则，‎ 解得：或 ‎18.解：（1）函数f（x）=x，g（x）=x2+2x-2，则f′（x）=1，g′（x）=2x+2． …………1分 由f（x）=g（x）且f′（x）= g′（x），得 ……………………………………2分 ‎，此方程组无解， ……………………………………4分 因此，f（x）与g（x）不存在“S”点． ……………………………………5分 ‎（2）函数，， ……………………………………6分 则． ……………………………………7分 设x0为f（x）与g（x）的“S”点，由f（x0）=g（x0）且f′（x0）=g′（x0），得 ‎，即，（*） ……………………………………10分 得，即，则．‎ 当时，满足方程组（*），即为f（x）与g（x）的“S”点．‎ 因此，a的值为． ……………………………………12分 ‎19. 解：（1）由,得 ‎， ……………………………………1分 即，故， ……………………3分 所以,， ……………………………………4分 由,． ………………………………………………………………5分 ‎（2）由（1）得，即， ………………………………………6分 又为锐角三角形，故，从而， ………………7分 由，所以，故,， ‎ 所以 ‎．……9分 由，所以，‎ 所以，………………………………………………………………11分 即． ………………………………………………………………12分 ‎20. 解:（1）的定义域为，.．……1分 ‎（i）若，则，当且仅当，时，所以在单调递减. ………………………………………………………………3分 ‎（ii）若，令得，或. ……4分 当时，；………………………5分 当时， .………………………6分 所以在单调递减，‎ 在单调递增.‎ ‎（2）由（1）知，存在两个极值点当且仅当.‎ 由于的两个极值点满足，所以，…………………7分 不妨设，则.由于 ‎，‎ 所以等价于. …………………10分 设函数，由（1）知，在单调递减，又，从而当时，.‎ 所以，即. …………………12分 ‎21. （1）①当时，自驾群体人均通勤时间为分钟，…………………1分 公交群体人均通勤时间为分钟，此时公交群体人均通勤时间大于自驾群体人均通勤时间。‎ ‎②当时：…………………12分…………………12分 令，得。………………………………………………3分 解得：或，‎ 所以当时，自驾群体的人均通勤时间大于分钟， …………………5分 ‎ 此时公交群体的人均通勤时间少于自驾群体的人均通勤时间。‎ 综上所述，当时，公交群体的人均通勤时间少于自驾群体的人均通勤时间。‎ ‎（2）当时，，…………………6分 当时，，‎ 所以， ………………8分 所以，‎ 当时，。‎ 所以当时，；‎ 当时，，‎ 则在上单调递减，‎ 当时，，‎ 则在上单调递增。 ……………………………………10分 表示当自驾群体的范围在时，上班族的人均通勤时间随自驾群体的增加而减少；当自驾群体占比为时，人均通勤时间为最小值；当自驾群体超过时，上班族的人均通勤时间随自驾群体的增多而增加。 …………………12分 ‎22. 解： （1）由，得的直角坐标方程为…3分 ‎（2）由（1）知是圆心为，半径为的圆．‎ 由题设知，是过点且关于轴对称的两条射线．记轴右边的射线为，‎ 轴左边的射线为．由于在圆的外面，故与有且仅有三个公共点等价于与只有一个公共点且与有两个公共点，或与只有一个公共点且与有两个公共点．‎ 当与只有一个公共点时，到所在直线的距离为，所以，故或． …………………………………5分 经检验，当时，与没有公共点；当时，与只有一个公共点，与有两个公共点．‎ 当与只有一个公共点时，到所在直线的距离为，所以，故或． …………………………………7分 经检验，当时，与没有公共点；当时，与没有公共点．‎ 综上，所求的方程为． …………………………………10分