- 2021-07-01 发布 |
- 37.5 KB |
- 7页

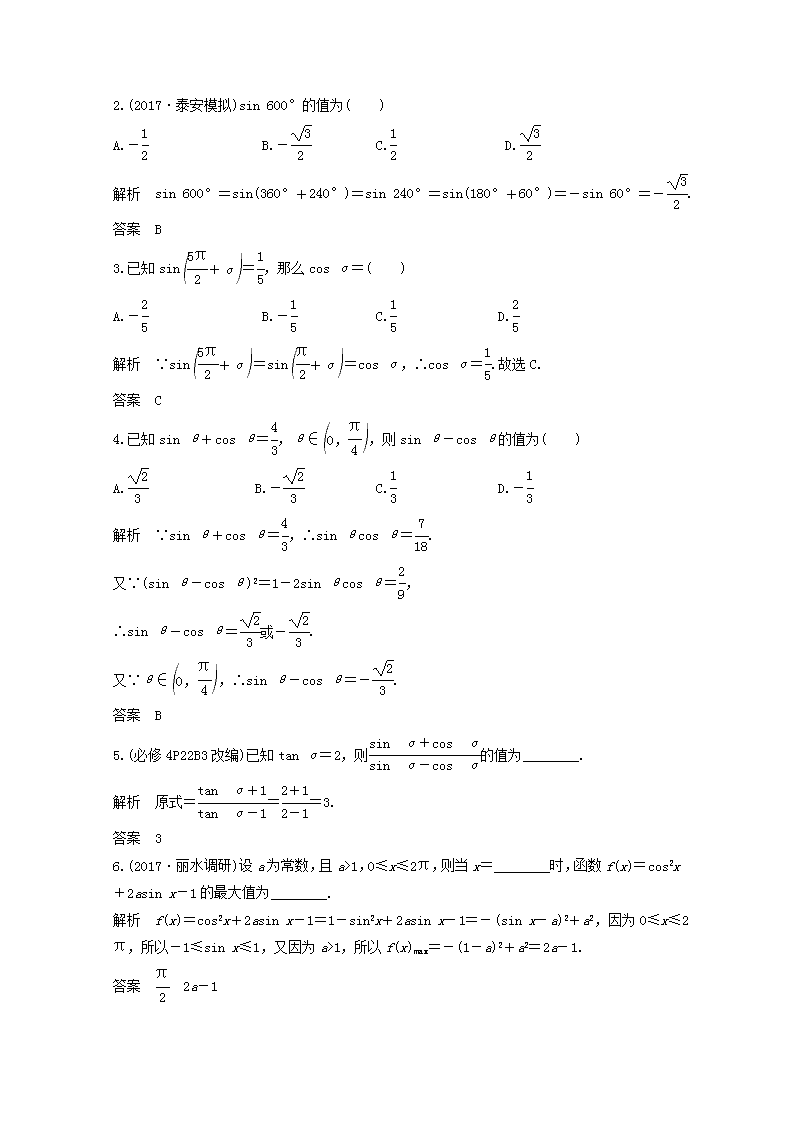

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
【数学】2018届一轮复习人教A版 同角三角函数的基本关系式与诱导公式 学案
第2讲 同角三角函数的基本关系式与诱导公式 最新考纲 1.理解同角三角函数的基本关系式:sin2α+cos2α=1,=tan α;2.能利用单位圆中的三角函数线推导出±α,π±α的正弦、余弦、正切的诱导公式. 知 识 梳 理 1.同角三角函数的基本关系 (1)平方关系:sin2α+cos2α=1. (2)商数关系:=tan__α. 2.三角函数的诱导公式 公式 一 二 三 四 五 六 角 2kπ+α(k∈Z) π+α -α π-α -α +α 正弦 sin α -sin__α -sin__α sin__α cos__α cos__α 余弦 cos α -cos__α cos__α -cos__α sin__α -sin__α 正切 tan α tan__α -tan__α -tan__α 口诀 函数名不变,符号看象限 函数名改变, 符号看象限 诊 断 自 测 1.判断正误(在括号内打“√”或“×”) (1)sin(π+α)=-sin α成立的条件是α为锐角.( ) (2)六组诱导公式中的角α可以是任意角.( ) (3)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.( ) (4)若sin(kπ-α)=(k∈Z),则sin α=.( ) 解析 (1)对于α∈R,sin(π+α)=-sin α都成立. (4)当k为奇数时,sin α=, 当k为偶数时,sin α=-. 答案 (1)× (2)√ (3)√ (4)× 2.(2017·泰安模拟)sin 600°的值为( ) A.- B.- C. D. 解析 sin 600°=sin(360°+240°)=sin 240°=sin(180°+60°)=-sin 60°=-. 答案 B 3.已知sin=,那么cos α=( ) A.- B.- C. D. 解析 ∵sin=sin=cos α,∴cos α=.故选C. 答案 C 4.已知sin θ+cos θ=,θ∈,则sin θ-cos θ的值为( ) A. B.- C. D.- 解析 ∵sin θ+cos θ=,∴sin θcos θ=. 又∵(sin θ-cos θ)2=1-2sin θcos θ=, ∴sin θ-cos θ=或-. 又∵θ∈,∴sin θ-cos θ=-. 答案 B 5.(必修4P22B3改编)已知tan α=2,则的值为________. 解析 原式===3. 答案 3 6.(2017·丽水调研)设a为常数,且a>1,0≤x≤2π,则当x=________时,函数f(x)=cos2x+2asin x-1的最大值为________. 解析 f(x)=cos2x+2asin x-1=1-sin2x+2asin x-1=-(sin x-a)2+a2,因为0≤x≤2π,所以-1≤sin x≤1,又因为a>1,所以f(x)max=-(1-a)2+a2=2a-1. 答案 2a-1 考点一 同角三角函数基本关系式的应用 【例1】 (1)(2015·福建卷)若sin α=-,且α为第四象限角,则tan α的值等于( ) A. B.- C. D.- (2)(2017·东阳模拟)已知sin αcos α=,且<α<,则cos α-sin α的值为( ) A.- B. C.- D. (3)(2016·全国Ⅲ卷)若tan α=,则cos2α+2sin 2α=( ) A. B. C.1 D. 解析 (1)∵sin α=-,且α为第四象限角,∴cos α==,∴tan α==-,故选D. (2)∵<α<, ∴cos α<0,sin α<0且cos α>sin α, ∴cos α-sin α>0. 又(cos α-sin α)2=1-2sin αcos α=1-2×=, ∴cos α-sin α=. (3)tan α=,则cos2α+2sin 2α===. 答案 (1)D (2)B (3)A 规律方法 (1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tan α可以实现角α的弦切互化. (2)应用公式时注意方程思想的应用:对于sin α+cos α,sin αcos α,sin α-cos α这三个式子,利用(sin α±cos α)2=1±2sin αcos α,可以知一求二. (3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α. 【训练1】 (1)已知sin α-cos α=,α∈(0,π),则tan α=( ) A.-1 B.- C. D.1 (2)若3sin α+cos α=0,则的值为( ) A. B. C. D.-2 解析 (1)由 得:2cos2α+2cos α+1=0, 即=0,∴cos α=-. 又α∈(0,π),∴α=, ∴tan α=tan =-1. (2)3sin α+cos α=0⇒cos α≠0⇒tan α=-,== ==. 答案 (1)A (2)A 考点二 诱导公式的应用 【例2】 (1)化简:sin(-1 200°)cos 1 290°+cos(-1 020°)·sin(-1 050°); (2)设f(α)=(1+2sin α≠0),求f的值. 解 (1)原式=-sin 1 200°cos 1 290°-cos 1 020°sin 1 050° =-sin(3×360°+120°)cos(3×360°+210°)-cos(2×360°+300°)sin(2×360°+330°) =-sin 120°cos 210°-cos 300°sin 330° =-sin(180°-60°)cos(180°+30°)-cos(360°-60°)·sin(360°-30°)=sin 60°cos 30°+cos 60°sin 30°=×+×=1. (2)∵f(α)= ===, ∴f====. 规律方法 (1)诱导公式的两个应用 ①求值:负化正,大化小,化到锐角为终了. ②化简:统一角,统一名,同角名少为终了. (2)含2π整数倍的诱导公式的应用 由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cos α. 【训练2】 (1)已知A=+(k∈Z),则A的值构成的集合是( ) A.{1,-1,2,-2} B.{-1,1} C.{2,-2} D.{1,-1,0,2,-2} (2)化简:=______. 解析 (1)当k为偶数时,A=+=2; k为奇数时,A=-=-2. (2)原式= ===-1. 答案 (1)C (2)-1 考点三 诱导公式、同角三角函数关系式的综合应用 【例3】 (1)已知tan=,则tan=________. (2)(2017·温州模拟)已知cos=,且-π<α<-,则cos等于( ) A. B. C.- D.- 解析 (1)∵+=π, ∴tan=tan =-tan=-. (2)因为+=, 所以cos=sin=sin. 因为-π<α<-,所以-<α+<-. 又cos=>0,所以-<α+<-, 所以sin=- =-=-. 答案 (1)- (2)D 规律方法 (1)常见的互余的角:-α与+α;+α与-α;+α与-α等. (2)常见的互补的角:+θ与-θ;+θ与-θ等. 【训练3】 (1)已知sin=,则cos=________. (2)设函数f(x)(x∈R)满足f(x+π)=f(x)+sin x,当0≤x<π时,f(x)=0,则f=( ) A. B. C.0 D.- 解析 (1)∵+=, ∴cos=cos=sin=. (2)由f(x+π)=f(x)+sin x,得f(x+2π)=f(x+π)+sin(x+π)=f(x)+sin x-sin x=f(x), 所以f=f =f=f=f+sinπ. 因为当0≤x<π时,f(x)=0. 所以f=0+=. 答案 (1) (2)A [思想方法] 1.同角三角函数基本关系可用于统一函数;诱导公式主要用于统一角,其主要作用是进行三角函数的求值、化简和证明,已知一个角的某一三角函数值,求这个角的其它三角函数值时,要特别注意平方关系的使用. 2.三角求值、化简是三角函数的基础,在求值与化简时,常用方法有:(1)弦切互化法:主要利用公式tan x=进行切化弦或弦化切,如,asin2x+bsin xcos x+ccos2x等类型可进行弦化切.(2)和积转换法:如利用(sin θ±cos θ)2=1±2sin θcos θ的关系进行变形、转化.(3)巧用“1”的变换:1=sin2θ+cos2θ=cos2θ(1+tan2θ)=sin2θ=tan =…. [易错防范] 1.利用诱导公式进行化简求值时,可利用公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐. 特别注意函数名称和符号的确定. 2.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号. 3.注意求值与化简后的结果一般要尽可能有理化、整式化.查看更多