2020年高中数学第四章定积分的概念

2020年高中数学第四章定积分的概念

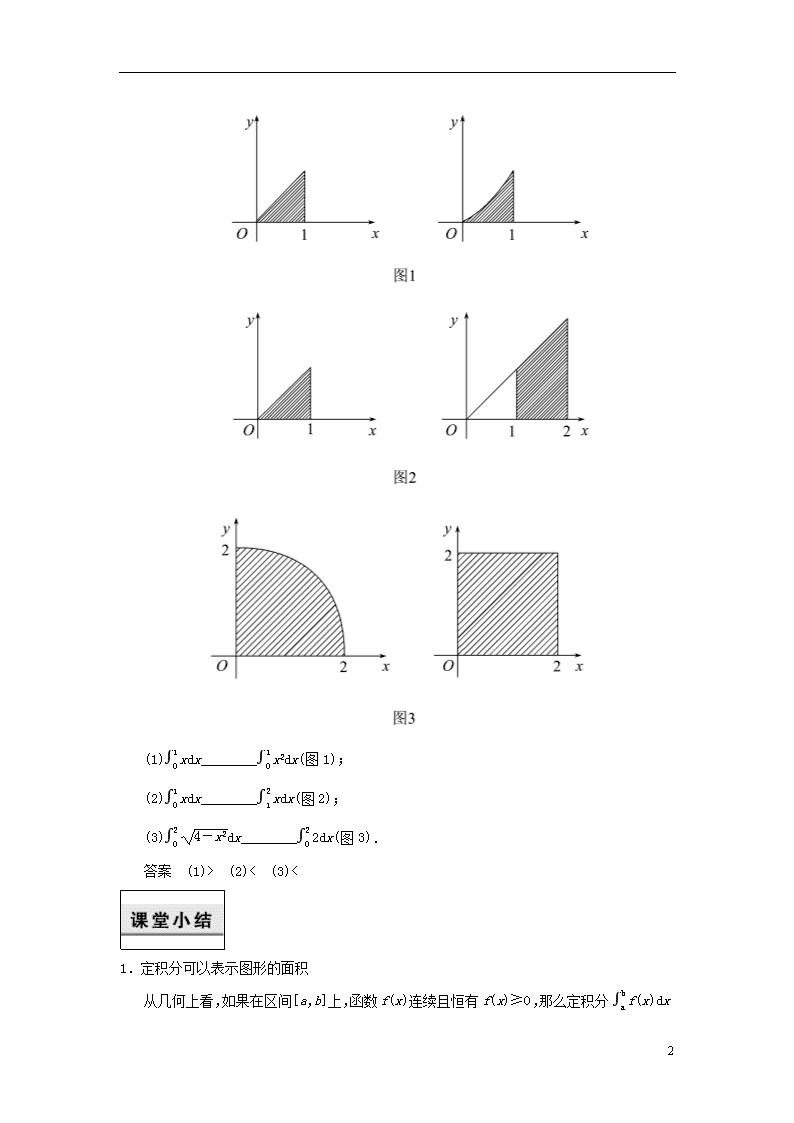
‎4.5.3‎‎ 定积分的概念 ‎1．定积分1dx的值等于 ‎(　　)‎ A．0 B．‎1 C. D．2‎ 答案　B ‎2．已知f(x)dx＝56，则 ‎(　　)‎ A.f(x)dx＝28‎ B.f(x)dx＝28‎ C.‎2f(x)dx＝56‎ D.f(x)dx＋f(x)dx＝56‎ 答案　D ‎3．如图所示，f1(x)dx＝M，f2(x)dx＝N，则阴影部分的面积为 ‎(　　)‎ A．M＋N B．M C．N D．M－N 答案　D ‎4．不用计算，根据图形，用不等号连接下列各式 ‎(　　)‎ 3‎ ‎(1)xdx________x2dx(图1)；‎ ‎(2)xdx________xdx(图2)；‎ ‎(3)dx________2dx(图3)．‎ 答案　(1)>　(2)<　(3)<‎ ‎1．定积分可以表示图形的面积 从几何上看，如果在区间[a，b]上，函数f(x)连续且恒有f(x)≥0，那么定积分f 3‎ ‎(x)dx就表示由直线x＝a，x＝b(a≠b)，y＝0和曲线y＝f(x)所围成的曲边梯形的面积，这就是定积分f(x)dx的几何意义．‎ ‎2．定积分表示图形面积的代数和 被积函数是正的，定积分的值也为正，如果被积函数是负的，函数曲线在x轴之下，定积分的值就是带负号的曲边梯形的面积．当被积函数在积分区间上有正有负时，定积分就是x轴之上的正的面积与x轴之下的负的面积的代数和．‎ ‎3．此外，定积分还有更多的实际意义，比如在物理学中，可以用定积分表示功、路程、压力、体积等．‎ ‎4．定积分是一个数值(极限值)，它的值仅仅取决于被积函数与积分的上、下限，而与积分变量用什么字母表示无关，即f(x)dx＝f(u)du＝f(t)dt＝…(称为积分形式的不变性)，另外定积分f(x)dx与积分区间[a，b]息息相关，不同的积分区间，所得的值也不同，例如(x2＋1)dx与(x2＋1)dx的值就不同.‎ 3‎