- 2021-07-01 发布 |
- 37.5 KB |
- 26页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届山东师大附中高三上学期第一次模拟数学试卷(理科)(解析版)
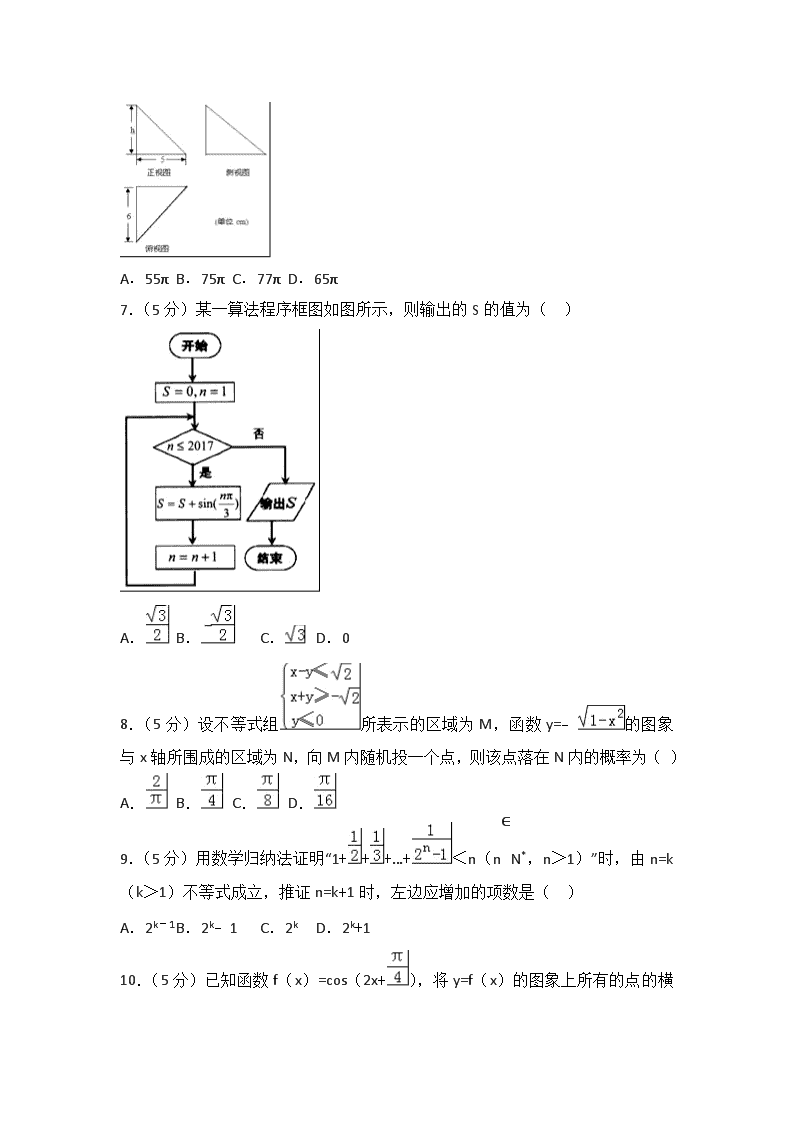
2017-2018学年山东师大附中高三(上)第一次模拟数学试卷(理科) 一、选择题:本题共12小题,每小题5分,共60分.在每题给出的四个选项中,有且仅有一项是符合要求的. 1.(5分)已知集合A={1,3,4,5},集合B={x∈Z|x2﹣4x﹣5<0},则A∩B的子集个数为( ) A.2 B.4 C.8 D.16 2.(5分)计算: =( ) A.2 B.﹣2 C.2i D.﹣2i 3.(5分)在下列区间中,使函数存在零点的是( ) A.(0,1) B.(1,2) C.(2,e) D.(3,4) 4.(5分)设随机变量X服从正态分布N(0,1),P(X>1)=p,则P(X>﹣1)=( ) A.p B.1﹣p C.1﹣2p D.2p 5.(5分)调查表明,酒后驾驶是导致交通事故的主要原因,交通法规规定:驾驶员在驾驶机动车时血液中酒精含量不得超过0.2mg/ml.如果某人喝了少量酒后,血液中酒精含量将迅速上升到0.8mg/ml,在停止喝酒后,血液中酒精含量就以每小时50%的速度减少,则他至少要经过( )小时后才可以驾驶机动车. A.1 B.2 C.3 D.4 6.(5分)如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( ) A.55π B.75π C.77π D.65π 7.(5分)某一算法程序框图如图所示,则输出的S的值为( ) A. B. C. D.0 8.(5分)设不等式组所表示的区域为M,函数y=﹣的图象与x轴所围成的区域为N,向M内随机投一个点,则该点落在N内的概率为( ) A. B. C. D. 9.(5分)用数学归纳法证明“1+++…+<n(n∈N*,n>1)”时,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项数是( ) A.2k﹣1 B.2k﹣1 C.2k D.2k+1 10.(5分)已知函数f(x)=cos(2x+ ),将y=f(x)的图象上所有的点的横坐标缩短为原来的倍,纵坐标不变;再把所得的图象向右平移|φ|个单位长度,所得的图象关于原点对称,则φ的一个值是( ) A. B. C. D. 11.(5分)“a>4”是“方程x2+ax+a=0有两个负实数根”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 12.(5分)抛物线y2=2px(p>0)的焦点为F,准线为L,A、B是抛物线上的两个动点,且满足∠AFB=.设线段AB的中点M在L上的投影为N,则的最大值是( ) A. B.1 C. D. 二、填空题:本题共4小题,每小题5分,共20分. 13.(5分)已知两个单位向量,满足|+2|=,则,的夹角为. 14.(5分)若dx=a,则(x+)6展开式中的常数项为 . 15.(5分)已知,则= . 16.(5分)已知函数f(x)=(x2+ax+b)ex,当b<1时,函数f(x)在(﹣∞,﹣2),(1,+∞)上均为增函数,则的取值范围是 . 三、解答题:共70分.解答题应写出必要的文字说明、证明过程或演算步骤.第17~21题为必做题,每个试题考生都必须作答.第22、23题为选做题,考生根据要求作答.(一)必考题:共60分. 17.(12分)已知等差数列{an}满足a4=6,a6=10. (1)求数列{an}的通项公式; (2)设等比数列{bn}各项均为正数,其前n项和Tn,若b3=a3,T2=3,求Tn. 18.(12分)如图,在四棱锥中P﹣ABCD,底面ABCD为边长为的正方形,PA⊥BD. (1)求证:PB=PD; (2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小. 19.(12分)自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据: 产假安排(单位:周) 14 15 16 17 18 有生育意愿家庭数 4 8 16 20 26 (1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少? (2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择. ①求两种安排方案休假周数和不低于32周的概率; ②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望. 20.(12分)已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2,)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N (Ⅰ)求椭圆C的方程; (Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由. 21.(12分)已知函数f(x)=ax(lnx﹣1)(a≠0). (1)求函数y=f(x)的单调递增区间; (2)当a>0时,设函数g(x)=x3﹣f(x),函数h(x)=g′(x), ①若h(x)≥0恒成立,求实数a的取值范围; ②证明:ln(1×2×3×…×n)2e<12+22+32+…+n2(n∈N*). (二)选做题:共10分.请考生在第22、23题中任选一题作答至选做题答题区域,标清题号.如果多做,则按所做第一题计分.[选修4-4:坐标系与参数方程](本题满分10分) 22.(10分)已知直线l的参数方程:(t为参数),曲线C的参数方程:(α为参数),且直线交曲线C于A,B两点. (Ⅰ)将曲线C的参数方程化为普通方程,并求θ=时,|AB|的长度; (Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA|•|PB|的范围. [选修4-5:不等式选讲] 23.已知函数f(x)=log2(|x﹣1|+|x+2|﹣a). (Ⅰ)当a=7时,求函数f(x)的定义域; (Ⅱ)若关于x的不等式f(x)≥3的解集是R,求实数a的取值范围. 2017-2018学年山东师大附中高三(上)第一次模拟数学试卷(理科) 参考答案与试题解析 一、选择题:本题共12小题,每小题5分,共60分.在每题给出的四个选项中,有且仅有一项是符合要求的. 1.(5分)已知集合A={1,3,4,5},集合B={x∈Z|x2﹣4x﹣5<0},则A∩B的子集个数为( ) A.2 B.4 C.8 D.16 【分析】求出集合B,根据集合的基本运算进行求解即可. 【解答】解:B={x∈Z|x2﹣4x﹣5<0}=B={x∈Z|﹣1<x<5}={0,1,2,3,4}, 则A∩B={1,3,4}, 故A∩B的子集个数为23=8个, 故选:C 【点评】本题主要考查集合的基本运算以及集合关系的应用,根据条件求出A∩B是解决本题的关键. 2.(5分)计算: =( ) A.2 B.﹣2 C.2i D.﹣2i 【分析】先求出(1﹣i)2的值,代入所求式子,利用两个复数代数形式的乘除法,虚数单位i的幂运算性质进行化简. 【解答】解: ===2, 故选 A. 【点评】本题考查两个复数代数形式的乘除法,虚数单位i的幂运算性质, 两个复数相除,分子和分母同时乘以分母的共轭复数. 3.(5分)在下列区间中,使函数存在零点的是( ) A.(0,1) B.(1,2) C.(2,e) D.(3,4) 【分析】由函数零点的判定定理即可判断出. 【解答】解:∵f(1)=ln2﹣1<lne﹣1=0,f(2)=ln3﹣1>lne﹣1=0,∴f(1)f(2)<0. ∴函数f(x)在区间(1,2)上存在零点. 故选B. 【点评】熟练掌握函数零点的判定定理是解题的关键. 4.(5分)设随机变量X服从正态分布N(0,1),P(X>1)=p,则P(X>﹣1)=( ) A.p B.1﹣p C.1﹣2p D.2p 【分析】根据随机变量符合正态分布和正态分布的曲线关于x=0对称,得到一对对称区间的概率之间的关系,即P(X>1)=P(X<﹣1),得到要求的区间的概率. 【解答】解:∵随机变量X服从正态分布N(0,1), P(X>1)=p, ∴P(X<﹣1)=p, P(X>﹣1)=1﹣P(X<﹣1)=1﹣p, 故选B. 【点评】本题考查正态分布曲线的特点及曲线所表示的意义,考查曲线关于x=0对称时,对称轴两侧的对称区间上的概率之间的关系,本题的运算量比较小,是一个送分题目. 5.(5分)调查表明,酒后驾驶是导致交通事故的主要原因,交通法规规定:驾驶员在驾驶机动车时血液中酒精含量不得超过0.2mg/ml.如果某人喝了少量酒后,血液中酒精含量将迅速上升到0.8mg/ml,在停止喝酒后,血液中酒精含量就以每小时50%的速度减少,则他至少要经过( )小时后才可以驾驶机动车. A.1 B.2 C.3 D.4 【分析】设n个小时后才可以驾车,根据题意可知,每单位时间内酒精下降的量成等比数列,进而可得方程,求得n. 【解答】解:设n个小时后才可以驾车, 由题得方程0.8(1﹣50%)n=0.2 0.5n=,n=2 即至少要经过2小时后才可以驾驶机动车. 故答案为2 【点评】本题意实际问题为依托,主要考查了等比数列的性质及实际应用.考查了学生运用所学知识解决实际问题的能力. 6.(5分)如图中的三个直角三角形是一个体积为20cm3的几何体的三视图,则该几何体外接球的面积(单位:cm2)等于( ) A.55π B.75π C.77π D.65π 【分析】由三视图可知几何体为三棱锥,作出其直观图三棱锥A﹣BCD; 由三棱锥的体积求出h的值,把三棱锥还原为长方体, 长方体对角线的长是三棱锥外接球的直径2R,由此求出外接球的面积. 【解答】解:由三视图可知几何体为三棱锥,作出其直观图三棱锥A﹣BCD; 由三视图可知AB⊥平面BCD,BC⊥BD,BD=5,BC=6,AB=h, ∴三棱锥的体积V=××5×6h=20,∴h=4; 把三棱锥还原为长方体,如图所示; 则长方体对角线的长是三棱锥外接球的直径2R; ∴(2R)2=42+52+62=77, ∴三棱锥外接球的面积为S=4πR2=77π. 故选:C. 【点评】本题考查了三棱锥的结构特征以及多面体外接球的面积计算问题,是基础题. 7.(5分)某一算法程序框图如图所示,则输出的S的值为( ) A. B. C. D.0 【分析】由已知程序框图的功能是利用循环结构计算并输出变量S的值, 根据y=sin的周期性,即可求出S的值. 【解答】解:由已知程序框图的功能是利用循环结构计算并输出变量 S=sin+sin+sinπ+…+sin的值, 由于y=sin的周期为6,且同一周期内的6个函数值的累加和为0; 又2016÷6=336, 所以S=sin+sin+sinπ+…+sin=sin=sin=. 故选:A. 【点评】本题考查了程序框图的应用问题,是基础题. 8.(5分)设不等式组所表示的区域为M,函数y=﹣的图象与x轴所围成的区域为N,向M内随机投一个点,则该点落在N内的概率为( ) A. B. C. D. 【分析】作出平面区域,根据面积比得出概率. 【解答】解:作出图形如图所示: 则区域M为△ABC,区域N为单位圆的下半圆, 点O到直线x+y=﹣和直线x﹣y=的距离均为=1,故半圆与AB,BC相切. ∴向M内随机投一个点,则该点落在N内的概率为P=== . 故选B. 【点评】本题考查了几何概型的概率计算,属于基础题. 9.(5分)用数学归纳法证明“1+++…+<n(n∈N*,n>1)”时,由n=k(k>1)不等式成立,推证n=k+1时,左边应增加的项数是( ) A.2k﹣1 B.2k﹣1 C.2k D.2k+1 【分析】考查不等式左侧的特点,分母数字逐渐增加1,末项为,然后判断n=k+1时增加的项数即可. 【解答】解:左边的特点:分母逐渐增加1,末项为; 由n=k,末项为到n=k+1,末项为=,∴应增加的项数为2k. 故选C. 【点评】本题是基础题,考查数学归纳法证明问题的第二步,项数增加多少问题,注意表达式的形式特点,找出规律是关键. 10.(5分)已知函数f(x)=cos(2x+),将y=f(x)的图象上所有的点的横坐标缩短为原来的倍,纵坐标不变;再把所得的图象向右平移|φ|个单位长度,所得的图象关于原点对称,则φ的一个值是( ) A. B. C. D. 【分析】根据函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,诱导公式,求得φ的值. 【解答】解:已知函数f(x)=cos(2x+ ),将y=f(x)的图象上所有的点的横坐标缩短为原来的倍,纵坐标不变,可得y=cos(4x+)的图象, 再把所得的图象向右平移|φ|个单位长度,可得y=cos(4x﹣4|φ|+)的图象. 根据所得的图象关于原点对称,可得﹣4|φ|+=kπ+,k∈Z, 令k=﹣1,可得φ的一个值是, 故选:D. 【点评】本题主要考查函数y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题. 11.(5分)“a>4”是“方程x2+ax+a=0有两个负实数根”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 【分析】方程x2+ax+a=0有两个负实数根,则,解出即可判断出结论. 【解答】解:方程x2+ax+a=0有两个负实数根,则,解得a≥4, ∴“a>4”是“方程x2+ax+a=0有两个负实数根”的充分不必要条件. 故选:A. 【点评】本题考查了一元二次方程的实数根与判别式的关系、根与系数的关系、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题. 12.(5分)抛物线y2=2px(p>0)的焦点为F,准线为L,A、B是抛物线上的两个动点,且满足∠AFB=.设线段AB的中点M在L上的投影为N,则 的最大值是( ) A. B.1 C. D. 【分析】设|AF|=a,|BF|=b,连接AF、BF.由抛物线定义得2|MN|=a+b,由余弦定理可得|AB|2=(a+b)2﹣3ab,进而根据基本不等式,求得|AB|的取值范围,从而得到本题答案. 【解答】解:设|AF|=a,|BF|=b,连接AF、BF, 由抛物线定义,得|AF|=|AQ|,|BF|=|BP|, 在梯形ABPQ中,2|MN|=|AQ|+|BP|=a+b. 由余弦定理得, |AB|2=a2+b2﹣2abcos60°=a2+b2﹣ab, 配方得,|AB|2=(a+b)2﹣3ab, 又∵ab≤()2, ∴(a+b)2﹣3ab≥(a+b)2﹣(a+b)2=(a+b)2 得到|AB|≥(a+b). ∴≤1, 即的最大值为1. 故选:B. 【点评】 本题给出抛物线的弦AB对焦点F所张的角为直角,求AB中点M到准线的距离与AB比值的取值范围,着重考查了抛物线的定义与简单几何性质、梯形的中位线定理和基本不等式求最值等知识,属于中档题. 二、填空题:本题共4小题,每小题5分,共20分. 13.(5分)已知两个单位向量,满足|+2|=,则,的夹角为 . 【分析】利用向量的模的计算公式,求出向量的夹角即可. 【解答】解:因为|+2|=, 所以|+2|2==()2, 又,是两个单位向量, 所以, ∴=﹣, 又, 所以cos=, ,的夹角为. 故答案为. 【点评】本题考查向量的数量积的运算,向量的模的应用,考查计算能力. 14.(5分)若dx=a,则(x+)6展开式中的常数项为 160 . 【分析】先根据定积分求出a的值,再根据二项式定理即可求出展开式中的常数项. 【解答】解: dx=2lnx|=2(lne﹣ln1)=2=a, ∴(x+)6展开式中的常数项为C6323=160, 故答案为:160 【点评】本题考查了定积分和二项式定理的应用,属于基础题. 15.(5分)已知,则= . 【分析】根据三角恒等变换化简,得出sin(α+)的值,再利用二倍角公式求出的值. 【解答】解:∵, ∴sincosα﹣cossinα﹣cosα =﹣sinα﹣cosα =﹣sin(α+)=, ∴sin(α+)=﹣; ∴=1﹣2sin2(α+) =1﹣2× =. 故选:. 【点评】本题考查了三角恒等变换与二倍角公式的应用问题,是基础题. 16.(5分)已知函数f(x)=(x2+ax+b)ex,当b<1时,函数f(x)在(﹣∞,﹣2),(1,+∞)上均为增函数,则的取值范围是 (﹣3,﹣] . 【分析】根据求导公式求出函数的导数,在根据二次函数图象求出a,b的取值范围,绘制出a,b的取值范围,根据线性规划求出其取值范围. 【解答】解:由f′(x)=[x2+(a+2)x+a+b]ex 函数f(x)在(﹣∞,﹣2),(1,+∞)增函数, ∴x2+(a+2)x+a+b>0恒成立, ∴, ∴, 画出满足条件的平面区域,如图所示: , 由,解得B(1,1), 由,解得C(﹣1,﹣1), 结合图象的几何意义表示过A(2,﹣2)与平面区域内的点的直线的斜率, 而KAB=﹣3,KAC=﹣, 故的取值范围是(﹣3,﹣], 故答案为:(﹣3,﹣]. 【点评】考察学生函数求导、二次函数的性质及线性规划问题,属于中档题. 三、解答题:共70分.解答题应写出必要的文字说明、证明过程或演算步骤.第17~21题为必做题,每个试题考生都必须作答.第22、23题为选做题,考生根据要求作答.(一)必考题:共60分. 17.(12分)已知等差数列{an}满足a4=6,a6=10. (1)求数列{an}的通项公式; (2)设等比数列{bn}各项均为正数,其前n项和Tn,若b3=a3,T2=3,求Tn. 【分析】(1)利用等差数列的通项公式可把已知条件用a1,d表示,解方程可得a1,d从而可求an (2)由(1)可得an=2n﹣2,把已知可转化为,解方程可得b1,q,代入等比数列的求和公式. 【解答】解:(1)设等差数列{an}的公差为d,首项为a, ∵a4=6,a6=10,∴(3分) 解得(5分) ∴数列{an}的通项公式an=a1+(n﹣d)d=2n﹣2.(6分) (2)设各项均为正数的等比数列{bn}的公比为q(q>0) ∵an=2n﹣2, ∴a3=4, ∵a3=b3, ∴b3=4 即(8分) 解得或舍(10分) ∴.(12分) 【点评】本小题主要考查等差、等比数列的通项公式以及等比数列的前n项和公式,属于对基本定义、基本公式的简单运用的考查,试题难度不大. 18.(12分)如图,在四棱锥中P﹣ABCD,底面ABCD为边长为的正方形,PA⊥BD. (1)求证:PB=PD; (2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小. 【分析】(1)连接AC,BD交于点O,连结PO,则AC⊥BD,结合PA⊥BD得出BD⊥平面PAC,故而BD⊥PO,又O为BD的中点,得出OP为BD的中垂线,得出结论; (2)设PD的中点为Q,连接AQ,EQ,证明四边形AQEF是平行四边形,于是AQ⊥平面PCD,通过证明CD⊥平面PAD得出CD⊥PA,结合PA⊥BD得出PA⊥平面ABCD,以A为原点建立空间直角坐标系,则直线PB与平面PCD所成角的正弦值等于|cos<>|,从而得出线面角的大小. 【解答】解:(1)连接AC,BD交于点O,连结PO. ∵底面ABCD是正方形, ∴AC⊥BD,OB=OD. 又PA⊥BD,PA⊂平面PAC,AC⊂平面PAC,PA∩AC=A, ∴BD⊥平面PAC,∵PO⊂平面PAC, ∴BD⊥PO. 又OB=OD, ∴PB=PD. (2)设PD的中点为Q,连接AQ,EQ, 则EQ∥CD,EQ=CD,又AF∥CD,AF==, ∴EQ∥AF,EQ=AF, ∴四边形AQEF为平行四边形,∴EF∥AQ, ∵EF⊥平面PCD,∴AQ⊥平面PCD, ∴AQ⊥PD,∵Q是PD的中点, ∴AP=AD=. ∵AQ⊥平面PCD,∴AQ⊥CD, 又AD⊥CD,AQ∩AD=A, ∴CD⊥平面PAD,∴CD⊥PA. 又BD⊥PA,BD∩CD=D, ∴PA⊥平面ABCD. 以A为坐标原点,以AB,AD,AP为坐标轴建立如图所示的空间直角坐标系, 则B(,0,0),P(0,0,),A(0,0,0),Q(0,,). ∴=(0,,),=(,0,﹣). ∵AQ⊥平面PCD,∴为平面PCD的一个法向量. ∴cos<>==﹣. 设直线PB与平面PCD所成角为θ, 则sinθ=|cos<>|=. ∴直线PB与平面PCD所成角为. 【点评】本题考查了线面垂直的判定与性质,线面角的计算,空间向量的应用,属于中档题. 19.(12分)自2016年1月1日起,我国全面二孩政策正式实施,这次人口与生育政策的历史性调整,使得“要不要再生一个”“生二孩能休多久产假”等成为千千万万个家庭在生育决策上避不开的话题.为了解针对产假的不同安排方案形成的生育意愿,某调查机构随机抽取了200户有生育二胎能力的适龄家庭进行问卷调查,得到如下数据: 产假安排(单位:周) 14 15 16 17 18 有生育意愿家庭数 4 8 16 20 26 (1)若用表中数据所得的频率代替概率,面对产假为14周与16周,估计某家庭有生育意愿的概率分别为多少? (2)假设从5种不同安排方案中,随机抽取2种不同安排分别作为备选方案,然后由单位根据单位情况自主选择. ①求两种安排方案休假周数和不低于32周的概率; ②如果用ξ表示两种方案休假周数和.求随机变量ξ的分布及期望. 【分析】(1)由表中信息可知,利用等可能事件概率计算公式能求出当产假为14周时某家庭有生育意愿的概率和当产假为16周时某家庭有生育意愿的概率. (2)①设“两种安排方案休假周数和不低于32周”为事件A,由已知从5种不同安排方案中,随机地抽取2种方案选法共有10种,由此利用列举法能求出其和不低于32周的概率. ②由题知随机变量ξ的可能取值为29,30,31,32,33,34,35.分别求出相应的概率,由此能求出ξ的分布列和E(ξ). 【解答】解:(1)由表中信息可知,当产假为14周时某家庭有生育意愿的概率为; 当产假为16周时某家庭有生育意愿的概率为…(2分) (2)①设“两种安排方案休假周数和不低于32周”为事件A, 由已知从5种不同安排方案中,随机地抽取2种方案选 法共有(种), 其和不低于32周的选法有(14、18)、(15、17)、(15、18)、(16、17)、(16、18)、(17、18),共6种, 由古典概型概率计算公式得…(6分) ②由题知随机变量ξ的可能取值为29,30,31,32,33,34,35. ,, , 因而ξ的分布列为 ξ 29 30 31 32 33 34 35 P 0.1 0.1 0.2 0.2 0.2 0.1 0.1 所以E(ξ)=29×0.1+30×0.1+31×0.2+32×0.2+33×0.2+34×0.1+35×0.1=32,…(12分) 【点评】本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意等可能事件概率计算公式的合理运用. 20.(12分)已知椭圆C的中心在坐标原点,焦点在x轴上,左顶点为A,左焦点为F1(﹣2,0),点B(2,)在椭圆C上,直线y=kx(k≠0)与椭圆C交于E,F两点,直线AE,AF分别与y轴交于点M,N (Ⅰ)求椭圆C的方程; (Ⅱ)在x轴上是否存在点P,使得无论非零实数k怎样变化,总有∠ MPN为直角?若存在,求出点P的坐标,若不存在,请说明理由. 【分析】(Ⅰ)由题意可设椭圆标准方程为+=1(a>b>0),结合已知及隐含条件列关于a,b,c的方程组,求解方程组得到a2,b2的值,则椭圆方程可求; (Ⅱ)设F(x0,y0),E(﹣x0,﹣y0),写出AE、AF所在直线方程,求出M、N的坐标,得到以MN为直径的圆的方程,由圆的方程可知以MN为直径的圆经过定点(±2,0),即可判断存在点P. 【解答】解:(Ⅰ)由题意可设椭圆方程为+=1(a>b>0), 则c=2,a2﹣b2=c2, +=1,解得:a2=8,b2=4. 可得椭圆C的方程为+=1; (Ⅱ)如图,设F(x0,y0),E(﹣x0,﹣y0),则+=1,A(﹣2,0), AF所在直线方程y=(x+2), 取x=0,得y=, ∴N(0,), AE所在直线方程为y=(x+2), 取x=0,得y=. 则以MN为直径的圆的圆心坐标为(0,), 半径r=, 圆的方程为x2+(y﹣)2==,即x2+(y+)2=. 取y=0,得x=±2. 可得以MN为直径的圆经过定点(±2,0). 可得在x轴上存在点P(±2,0), 使得无论非零实数k怎样变化,总有∠MPN为直角. 【点评】本题考查椭圆的方程和简单性质,考查直线与圆位置关系的应用,考查整体运算思想方法,是中档题. 21.(12分)已知函数f(x)=ax(lnx﹣1)(a≠0). (1)求函数y=f(x)的单调递增区间; (2)当a>0时,设函数g(x)=x3﹣f(x),函数h(x)=g′(x), ①若h(x)≥0恒成立,求实数a的取值范围; ②证明:ln(1×2×3×…×n)2e<12+22+32+…+n2(n∈N*). 【分析】(1)求出函数f(x)的导数,对a讨论,分a>0,a<0,由导数大于0,解得增区间; (2)①当a>0时,求出g(x)的导数,由题意可得≥的最大值,求出右边函数的导数,求得单调区间、极值和最值,即可得到所求a的范围; ②由①可得<,x∈N,可得2elnn<n2,由累加法和对数的运算性质即可得证. 【解答】解:(1)函数f(x)=ax(lnx﹣1)的导数为f′(x)=a(lnx﹣1)+a=alnx, 当a>0时,x>1时,f′(x)>0,f(x)递增;0<x<1时,f′(x)<0,f(x)递减; 当a<0时,0<x<1时,f′(x)>0,f(x)递增;x>1时,f′(x)<0,f(x)递减. 即有a>0,f(x)的递增区间为(1,+∞); a<0时,f(x)的递增区间为(0,1); (2)①当a>0时,设函数g(x)=x3﹣f(x)=x3﹣ax(lnx﹣1), 函数h(x)=g′(x)=x2﹣alnx,x>0, h(x)≥0恒成立,即为≥的最大值, 由y=的导数为,当x>时,函数y递减; 当0<x<时,函数y递增,即有x=取得最大值, 则有≥,解得0<a≤e; ②证明:由①可得<,x∈N, 即有2elnn<n2, 可得2e(ln1+ln2+ln3+…+lnn)<12+22+32+…+n2, 则ln(1•2•3…n)2e<12+22+32+…+n2(n∈N*). 【点评】本题考查导数的运用:求单调区间和极值、最值,考查不等式成立问题的解法,注意运用参数分离和构造函数,考查不等式的证明,注意运用已知不等式,考查运算和推理能力,属于中档题. (二)选做题:共10分.请考生在第22、23题中任选一题作答至选做题答题区域,标清题号.如果多做,则按所做第一题计分.[选修4-4:坐标系与参数方程](本题满分10分) 22.(10分)已知直线l的参数方程:(t为参数),曲线C的参数方程:(α为参数),且直线交曲线C于A,B两点. (Ⅰ)将曲线C的参数方程化为普通方程,并求θ=时,|AB|的长度; (Ⅱ)已知点P:(1,0),求当直线倾斜角θ变化时,|PA|•|PB|的范围. 【分析】(Ⅰ)利用三角函数的平方关系式,将曲线C的参数方程化为普通方程,求出直线AB的方程,代入,可得3x2﹣4x=0,即可求出|AB|的长度; (Ⅱ)直线参数方程代入,A,B对应的参数为t1,t2,则|PA|•|PB|=﹣t1t2,即可求出|PA|•|PB|的范围. 【解答】解:(Ⅰ)曲线C的参数方程:(α为参数),曲线C的普通方程为. 当θ=时,直线AB的方程为,y=x﹣1, 代入,可得3x2﹣4x=0,∴x=0或x= ∴|AB|=•=; (Ⅱ)直线参数方程代入,得(cos2θ+2sin2θ)t2+2tcosθ﹣1=0. 设A,B对应的参数为t1,t2,∴|PA|•|PB|=﹣t1t2==∈[,1]. 【点评】本题主要考查了参数方程化成普通方程,熟练掌握参数方程与直角坐标的互化公式是解题的关键. [选修4-5:不等式选讲] 23.已知函数f(x)=log2(|x﹣1|+|x+2|﹣a). (Ⅰ)当a=7时,求函数f(x)的定义域; (Ⅱ)若关于x的不等式f(x)≥3的解集是R,求实数a的取值范围. 【分析】(Ⅰ)当a=7时,利用对数函数的真数大于0,列出不等式,利用绝对值不等式转化为:代数不等式即可求函数f(x)的定义域; (Ⅱ)利用绝对值的几何意义,转化求解即可. 【解答】解:(Ⅰ)由题设知:|x﹣1|+|x+2|>7, 令x﹣1=0,x+2=0,解得x=1,x=﹣2,这就是两个分界点.把全体实数分成3个区间. 不等式的解集是以下不等式组解集的并集: ,或,或…(3分) 解得函数f(x)的定义域为(﹣∞,﹣4)∪(3,+∞); …(5分) (Ⅱ)不等式f(x)≥3即:|x﹣1|+|x+2|≥a+8, ∵x∈R时,恒有|x﹣1|+|x+2|≥|(x﹣1)﹣(x+2)|=3,…(8分) ∵不等式|x﹣1|+|x+2|≥a+8解集是R,∴a+8≤3, ∴a的取值范围是:(﹣∞,﹣5].…(10分) 【点评】本题考查函数恒成立,绝对值不等式的解法,考查转化思想以及计算能力.查看更多