- 2021-07-01 发布 |
- 37.5 KB |
- 12页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2021届新高考版高考数学一轮复习课件:§3-4 指数与指数函数(讲解部分)
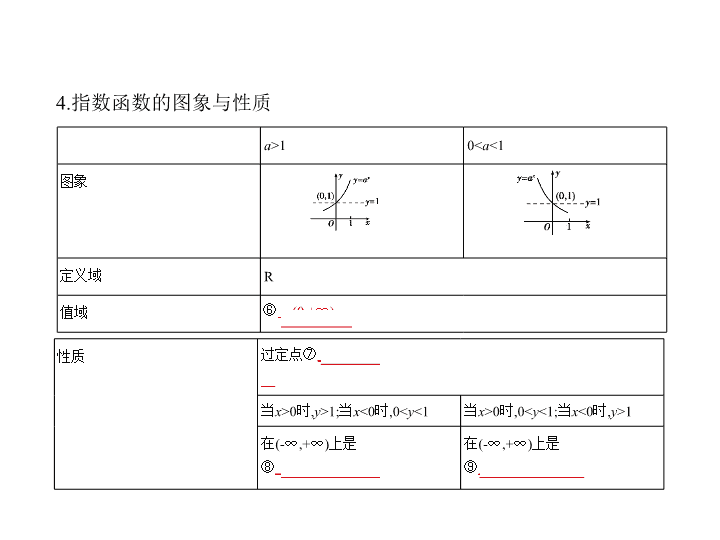
考点 指数与指数函数 1.根式的概念 2.两个重要公式 = 根式的概念 符号表示 备注 一般地,如果 x n = a ,那么 x 叫做 a 的 n 次方根 n >1且 n ∈N * 当 n 是奇数时,正数的 n 次方根是一个正数,负数的 n 次方根是一个负数 零的 n 次方根是零 当 n 是偶数时,正数的 n 次方根有两个,这两个数互为相反数 ± ( a >0) 负数没有偶次方根 考点清单 ( ) n =④ a (注意 a 必须使 有意义). 3.有理指数幂 (1)幂的有关概念 (i)正数的正分数指数幂: = ( a >0, m , n ∈N * ,且 n >1); (ii)正数的负分数指数幂: = = ( a >0, m , n ∈N * ,且 n >1); (iii)0的正分数指数幂等于⑤ 0 ,0的负分数指数幂没有意义. (2)有理指数幂的性质 (i) a r a s = a r + s ( a >0, r , s ∈Q); (ii)( a r ) s = a rs ( a >0, r , s ∈Q); (iii)( ab ) r = a r b r ( a >0, b >0, r ∈Q). a >1 0< a <1 图象 定义域 R 值域 ⑥ (0,+ ∞ ) 4.指数函数的图象与性质 性质 过定点⑦ (0,1) 当 x >0时, y >1;当 x <0时,0< y <1 当 x >0时,0< y <1;当 x <0时, y >1 在(- ∞ ,+ ∞ )上是 ⑧ 单调增函数 在(- ∞ ,+ ∞ )上是 ⑨ 单调减函数 5.指数函数在同一直角坐标系中的图象的相对位置与底数大小的关系如 图所示,其中0< c < d <1< a < b . 在 y 轴右侧,图象从上到下相应的底数由大变小; 在 y 轴左侧,图象从下到上相应的底数由大变小; 无论在 y 轴的左侧还是右侧,底数按逆时针方向变大. 考法一 指数式的大小比较 知能拓展 例1 下列各式比较大小正确的是 ( ) A.1.7 2.5 >1.7 3 B.0.6 -1 >0.6 2 C.0.8 -0.1 >1.25 0.2 D.1.7 0.3 <0.9 3.1 解题导引 解析 A中,∵函数 y =1.7 x 在R上是增函数,2.5<3,∴1.7 2.5 <1.7 3 .故A错误. B中,∵ y =0.6 x 在R上是减函数,-1<2,∴0.6 -1 >0.6 2 .故B正确. C中,∵(0.8) -1 =1.25, y =1.25 x 在R上是增函数,0.1<0.2,∴1.25 0.1 <1.25 0.2 ,即0.8 -0.1 <1.25 0.2 .故C错误.D中,∵函数 y =1.7 x 在R上是增函数,且0.3>0,∴1.7 0.3 >1.7 0 =1,又函数 y =0.9 x 在R上是减函数,且3.1>0,∴0<0.9 3.1 <0.9 0 =1.∴1.7 0.3 >0.9 3.1 .故D错误. 答案 B 方法总结 指数式值大小比较的常见类型:同底不同指数,同指数不同底, 底和指数均不相同.指数式值的大小比较的常用方法:(1)化为相同指数或 相同底数后利用相应函数的单调性,(2)作差或作商法,(3)利用中间量(0或1 等)分段. 考法二 指数(型)函数的图象和性质 例2 已知函数 y = . (1)作出函数图象; (2)由图象指出其单调区间; (3)由图象指出当 x 取什么值时有最值. 解题导引 解析 (1)由函数解析式可得 y = = 其图象分成两部分: 一部分是 y = ( x ≥ -2)的图象,由下列变换可得到: y = 的图象 y = 的图象; 另一部分是 y =2 x +2 ( x <-2)的图象,由下列变换可得到: y =2 x 的图象 y =2 x +2 的图象,如图(实线)为函数 y = 的图象. (2)由(1)中图象观察知函数的单调增区间为(- ∞ ,-2],单调减区间为(-2,+ ∞ ). (3)由(1)中图象观察知, x =-2时,函数 y = 取大值,最大值为1,没有最小值. 方法总结 (1)指数型复合函数的图象 对于指数型复合函数的图象问题,一般从最基本的指数函数的图象入手,通 过平移、伸缩、对称变换而得到.需特别注意底数 a >1与0< a <1两种不同情 况. (2)对于指数型复合函数图象问题,先求出定义域,对函数式进行化简变形, 转化成分段函数,画其图象. 例3 如果函数 f ( x )= a x ( a x -3 a 2 -1)( a >0,且 a ≠ 1)在区间[0,+ ∞ )上是增函数.求 实数 a 的取值范围. 解析 由题意得 f ( x )=( a x ) 2 -(3 a 2 +1) a x ,令 t = a x , t >0,则 f ( t )= t 2 -(3 a 2 +1) t ( t >0).当 a >1 时, t = a x 在[0,+ ∞ )上为增函数,此时 t ≥ 1,而对于 f ( t )而言, f ( t )图象的对称轴为 t = >2,故 f ( x )在[0,+ ∞ )上不可能为增函数; 当0< a <1时, t = a x 在[0,+ ∞ )上为减函数, 此时0< t ≤ 1,要使 f ( x )在[0,+ ∞ )上为增函数, 则 f ( t )在(0,1]上必为减函数,故 ≥ 1. ∴ a ≥ 或 a ≤ - ,∴ ≤ a <1. 方法总结 与指数函数有关的复合函数的单调区间的求解步骤 (1)求复合函数的定义域; (2)弄清函数是由哪些基本函数复合而成的; (3)分层逐一求解函数的单调区间; (4)求出复合函数的单调区间(注意“同增异减”). 例4 已知函数 f ( x )= a 2 x +2 a x -1( a >0且 a ≠ 1)在区间[-1,1]上的最大值为14.求 实数 a 的值. 解题导引 分0< a <1和 a >1两种情况讨论. 解析 f ( x )= a 2 x +2 a x -1=( a x +1) 2 -2. (1)当0< a <1时, a ≤ a x ≤ ,∴当 a x = 时, f ( x )取得最大值. ∴ -2=14,∴ =3或 =-5(舍去),∴ a = . (2)当 a >1时, ≤ a x ≤ a ,∴当 a x = a 时, f ( x )取得最大值. ∴( a +1) 2 -2=14,∴ a =3或 a =-5(舍去).综上可知,实数 a 的值为 或3. 方法总结 与指数函数有关的复合函数的定义域、值域的求法 (1)函数 y = a f ( x ) ( a >0,且 a ≠ 1)的定义域与 y = f ( x )的定义域相同; (2)先确定 f ( x )的值域,再根据指数函数的单调性确定 y = a f ( x ) ( a >0,且 a ≠ 1)的值域.查看更多