2019届二轮复习不等式学案（全国通用）

2019届二轮复习不等式学案（全国通用）

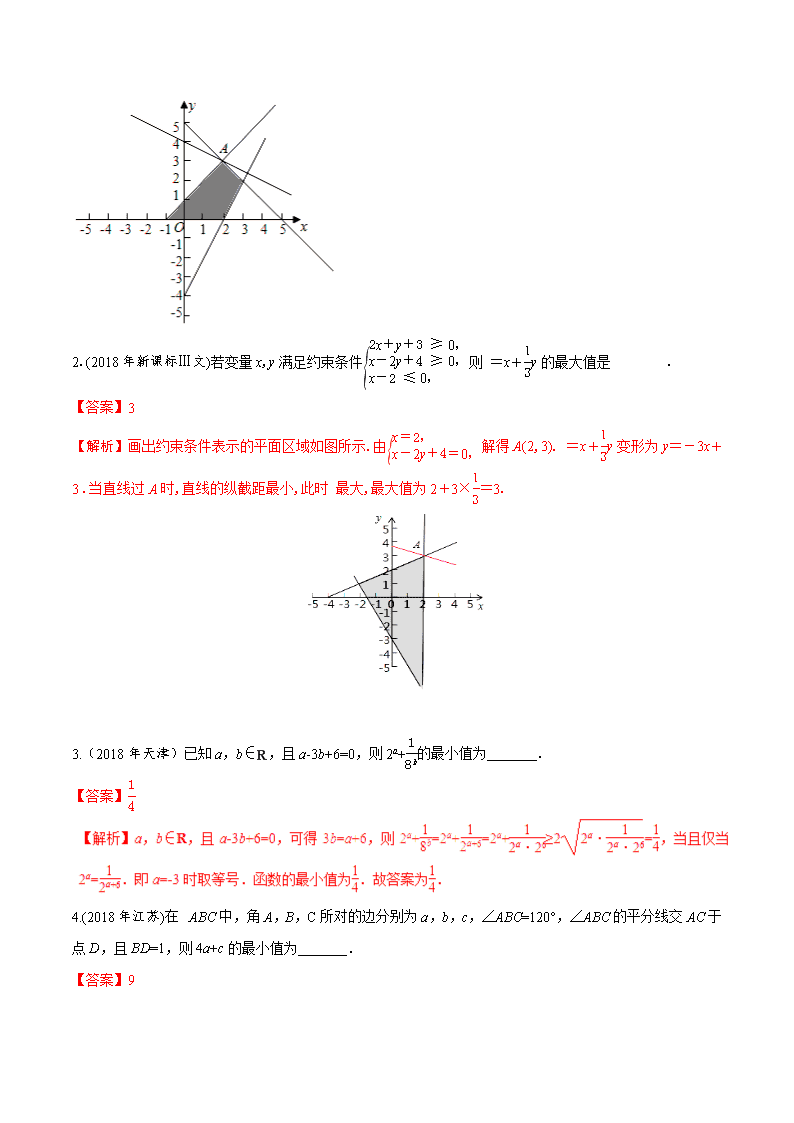
考情速递 ‎1真题感悟 真题回放 ‎1..（2018年天津）设变量x，y满足约束条件则目标函数 =3x+5y的最大值为（　　）‎ A．6 B．19 C．21 D．45‎ ‎【答案】C ‎2.(2018年新课标Ⅲ文)若变量x,y满足约束条件则 ＝x＋y的最大值是 .‎ ‎【答案】3‎ ‎【解析】画出约束条件表示的平面区域如图所示.由解得A(2,3). ＝x＋y变形为y＝－3x＋3 .当直线过A时,直线的纵截距最小,此时 最大,最大值为2＋3×＝3.‎ ‎3.（2018年天津）已知a，b∈R，且a-3b+6=0，则2a+的最小值为　 　．‎ ‎【答案】 ‎4.(2018年江苏)在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为　 　．‎ ‎【答案】9‎ ‎【解析】由题意得acsin 120°=asin 60°+csin 60°，即ac=a+c，得+=1，得4a+c=（4a+c）（+）=++5≥2+5=4+5=9，当且仅当=，即c=2a时，取等号．故答案为9．‎ ‎2热点题型 题型一：数、式的大小比较 例1．（2018年天津）已知a=log3，b=（），c=log，则a，b，c的大小关系为（　　）‎ A．a＞b＞c B．b＞a＞c C．c＞b＞a D．c＞a＞b ‎【答案】D ‎【提示】有指数有用对数函数比较大小，除了注意利用其性质外，还需要借助中间量比较大小。‎ 变式训练1‎ ‎1．（2018年北京）能说明“若a＞b，则＜”为假命题的一组a，b的值依次为　 　．‎ ‎【答案】a=1，b=-1 ‎ ‎【解析】当a＞0，b＜0时，满足a＞b，但＜为假命题，故答案可以是a=1，b=-1．‎ 题型二：一元二次不等式的解法学 ‎ 例2．（2018春•大同期末）已知不等式ax2+5x+b＞0的解集是{x|2＜x＜3}，则不等式bx2﹣5x+a＞0的解集是（　　）‎ A．{x|x＜﹣3或x＞﹣2} B．{x|x＜﹣或x＞﹣}‎ C．{x|﹣＜x＜﹣} D．{x|﹣3＜x＜﹣2}‎ ‎【分析】根据不等式与对应方程的关系，利用根与系数的关系求出a、b的值，再代入不等式bx2﹣5x+a＞0求解集即可．‎ ‎【答案】C ‎【点评】本题考查了一元二次不等式与对应方程的关系以及根与系数的关系的应用问题，是基础题目．‎ 变式训练4‎ ‎（2018春•台州期末）不等式x2+ax+b≤0（a，b∈R）的解集为{x|x1≤x≤x2}，若|x1|+|x2|≤2，则（　　）‎ A．|a+2b|≥2 B．|a+2b|≤2 C．|a|≥1 D．|b|≤1‎ ‎【答案】D ‎【解析】∵不等式x2+ax+b≤0（a，b∈R）的解集为{x|x1≤x≤x2}，‎ 则x1、x2是对应方程x2+ax+b=0的两个实数根；，x1x2=b，‎ 又|x1|+|x2|≤2，‎ 不妨令a=﹣1，b=0，则x1=0，x2=1，但|a+2b|=1，∴A选项不成立；‎ 令a=2，b=1，则x1=x2=1，但|a+2b|=4，B选项不成立；‎ 令a=0，b=﹣1，则x1=﹣1，x2=1，但|a|=0，C选项不成立；‎ b=x1•x2≤≤=1， D选项正确．‎ 故选：D．‎ 题型二：线性规划 例3．（2018年浙江）若x，y满足约束条件则 =x+3y的最小值是　 　，最大值是　 　．‎ 分析：画出可行域，利用数形结合思想直观解决。‎ ‎【答案】-2;8‎ ‎【规律方法】线性规划主要解决的是一次函数的最值问题，解决这一问题的条件主要有两个：一是线性约束条件，二是线性目标函数（其中）截距法是在A、B确定的情况下，若把 看成一个特定的常数，则线性目标函数就可看成一组斜率为的相互平行的直线系，相应的求最值就转化为求直线系在y轴上的截距的最值。‎ 对线性目标函数（A，B不同时为零）中B的符号一定要注意。当B>0时，若直线过可行域且在y轴上截距最大，则 值最大，在y轴上截距最小，则 值最小；当 学 ]‎ B<0时，若直线过可行域且在y轴上截距最大，则 值最小，在y轴上截距最小，则 值最大。‎ 变式训练5‎ ‎（2018•上城区校级模拟）已知不等式组表示的平面区域S的面积为9，若点P（x，y）∈S，则 =2x+y的最大值为（　　）‎ A．3 B．6 C．9 D．12‎ ‎【答案】C ‎ 学 ]‎ 当l经过点A时，目标函数 达到最大值，‎ ‎∴ 最大值=F（3，3）=9．‎ 故选：C．‎ ‎3.新题预测 ‎1.点P（x，y）是如图所示的三角形区域（包括边界）内任意一点，则的最小值为（　　）‎ A．﹣2 B．﹣ C．﹣ D．﹣‎ ‎【答案】B ‎【解析】的几何意义是可行域内的点与坐标原点连线的斜率，‎ 如图可知AO的斜率最小，A（﹣3，5），‎ 则的最小值为：﹣．‎ 故选：B．‎ ‎2现某小型服装厂锁边车间有锁边工10名，杂工15名，有7台电脑机，每台电脑机每天可给12件衣服锁边；有5台普通机，每台普通机每天可给10件衣服锁边．如果一天至少有100件衣服需要锁边，用电脑机每台需配锁边工1名，杂工2名，用普通机每台需要配锁边工1名，杂工1名．用电脑机给一件衣服锁边可获利8元，用普通机给一件衣服锁边可获利6元，则该服装厂锁边车间一天最多可获利（　　）元．‎ A．760 B．780 C．800 D．820‎ ‎【答案】B ‎【解析】设每天安排电脑机和普通机各x，y台，则一天可获利 =12×8x+10×6y=96x+60y，线性约束条件为，画出可行域（如图），‎ 可知当目标函数经过A（5，5）时， max=780．故选：B．‎ 不等式问题专项训练题 一选择题 ‎1.已知集合P＝{x|x2－x－2≤0}，Q＝{x|log2(x－1)≤1}，则(∁RP)∩Q等于(　　)‎ A．[2,3] B．(－∞，－1]∪[3，＋∞)‎ C．(2,3] D．(－∞，－1]∪(3，＋∞)‎ ‎【答案】C ‎【解析】依题意，得P＝{x|－1≤x≤2}，Q＝{x|1b>0,cbd B.acbc ‎【答案】B ‎【解析】根据c-d>0,由于a>b>0,两式相乘有-ac>-bd,ac0)的解集为(x1,x2),且x2-x1=15,则a等于(　　)‎ A. B. C. D.‎ ‎【答案】A ‎【解析】选A.由x2-2ax‎-8a2<0,得(x+‎2a)(x‎-4a)<0,因为a>0,‎ 所以不等式的解集为(-‎2a,‎4a),即x2=‎4a,x1=-‎2a,由x2-x1=15,得‎4a-(-‎2a)=15,解得a=.‎ ‎5. (2018·成都模拟)某企业拟生产甲、乙两种产品,已知每件甲产品的利润为3万元,每件乙产品的利润为2万元,且甲、乙两种产品都需要在A,B两种设备上加工,在每台设备A,每台设备B上加工1件甲产品所需工时分别为1 h和2 h,加工1件乙产品所需工时分别为2 h和1 h,A设备每天使用时间不超过4 h,B设备每天使用时间不超过5 h,则通过合理安排生产计划,该企业在一天内的最大利润是 (　　)‎ A.18万元 B.12万元 C.10万元 D.8万元 ‎【答案】D ‎【解析】设每天生产甲、乙两种产品分别为x件,y件,企业获得的利润为 万元,‎ 则x,y满足约束条件且 =3x+2y.‎ 作出不等式组表示的可行域,‎ 如图所示.由x∈N,y∈N可知最优解为(2,1),即生产甲产品2件,乙产品1件,可使企业获得最大利润,最大利润为8万元.‎ ‎6. 若不等式(a-a2)(x2+1)+x≤0对一切x∈(0,2]恒成立,则a的取值范围是 (　　)‎ A. B.‎ C.∪D.‎ ‎【答案】C ‎【解析】因为x∈(0,2],所以a2-a≥=.‎ 要使a2-a≥在x∈(0,2]时恒成立,则a2-a≥.‎ 由基本不等式得x+≥2,当且仅当x=1时,等号成立,即=,故a2-a≥,解得a≤或a≥.‎ ‎7.若实数满足条件，则的最小值为 A. B. C. D. ‎ ‎【答案】B 故答案为：B．‎ ‎8. 【天津市河东区2018届二模】已知正实数a,b,c满足当取最小值时，a+b-c的最大值为（ ）‎ A. 2 B. C. D. 学 ]‎ ‎【答案】C 解析：正实数a，b，c满足a2﹣ab+4b2﹣c=0，可得c=a2﹣ab+4b2，.当且仅当a=2b取得等号，则a=2b时，取得最小值，且c=6b2，∴a+b﹣c=2b+b﹣6b2=﹣6b2+3b=，当b=时，a+b﹣c有最大值为．故答案为：C ‎9. (2018·湖南东部六校联考)实数x，y满足(a＜1)，且 ＝2x＋y的最大值是最小值的4倍，则a＝ .‎ A. 1 B. 2 C. 3 D. ‎【答案】D ‎10. (2018·苏州期末)已知正数x，y满足x＋y＝1，则＋的最小值为 ．‎ A. B. 2 C. 3 D.5‎ ‎【答案】A ‎【解析】令x＋2＝a，y＋1＝b，则a＋b＝4(a＞2，b＞1)，所以＋＝＋＝(a＋b)＝≥(5＋4)＝，当且仅当a＝，b＝，即x＝，y＝时取等号．则＋的最小值为.‎ ‎11.【2018衡水金卷高三二模】已知实数满足约束条件当且仅当时，目标函数取大值，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】B 由，可得，因为当时，目标函数取得最大值，即取得最大值的最优解为点，观察图形可知，此时直线的斜率，所以实数的取值范围是，故选B.‎ ‎12. (2018·苏北四市联考)已知对满足x＋y＋4＝2xy的任意正实数x，y，都有x2＋2xy＋y2－ax－ay＋1≥0，则实数a的取值范围为 ．‎ A．(5,6) B. (3,4) C. (1,2) D. ‎【答案】D 法二：由x＋y＋4＝2xy≤得(x＋y)2－2(x＋y)－8≥0，又x，y是正实数，得x＋y≥4.原不等式整理可得(x＋y)2－a(x＋y)＋1≥0，令x＋y＝t，t≥4，则t2－at＋1≥0，t∈[4，＋∞)　( )恒成立，则a≤min＝，故实数a的取值范围是.‎ 二．填空题 ‎13. (2018·如东中学测试)已知函数f(x)＝则不等式f(x)≥x2的解集为 ．‎ ‎【答案】[－1,1] ‎ ‎【解析】当x≤0时，x＋2≥x2，解得－1≤x≤0；①‎ 当x>0时，－x＋2≥x2，解得0b>0，f(a)＝f(b)，则的最小值为 .‎ ‎【答案】‎ ‎15. 已知实数满足：，则的最大值为 ．‎ ‎【答案】‎ ‎【解析】分析：作出约束条件表示的可行域，令，变形为，将直线进行平移可得截距最大时即为所求.‎ 详解：作出不等式组：所表示的平面区域，目标函数，可变形为，‎ 将其进行平移可得，当直线过点A时，截距最大；‎ 联立，解得点坐标为，故，故答案为13．‎ ‎16． (2018·扬州中学检测)已知二次函数f(x)＝ax2－(a＋2)x＋1(a∈ )，且函数f(x)在(－2，－1)上恰有一个零点，则不等式f(x)＞1的解集为 ．‎ ‎【答案】(－1,0)‎