2018届二轮复习数学归纳法课件理(全国通用)
第六节
数学归纳法
【
知识梳理
】
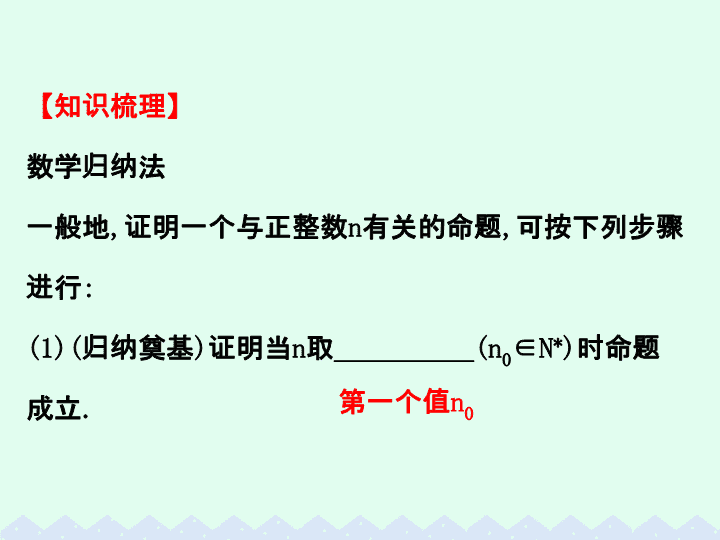
数学归纳法
一般地
,
证明一个与正整数
n
有关的命题
,
可按下列步骤
进行
:
(1)(
归纳奠基
)
证明当
n
取
__________(n
0
∈N
*
)
时命题
成立
.
第一个值
n
0
(2)(
归纳递推
)
假设当
n=k(k≥n
0
,k∈N
*
)
时命题成立
,
证明当
______
时命题也成立
.
只要完成这两个步骤
,
就可以断定命题对
____________
__________
都成立
,
上述证明方法叫做数学归纳法
.
n=k+1
从
n
0
开始的所
有正整数
n
【
特别提醒
】
1.
数学归纳法证题时
,
误把第一个值
n
0
认为是
1,
如证明多边形内角和定理
(n-2)π
时
,
初始值
n
0
=3.
2.
数学归纳法证题的关键是第二步
,
证题时应注意
:
(1)
必须利用归纳假设作基础
.
(2)
证明中可利用综合法、分析法、反证法等方法
.
(3)
解题时要搞清从
n=k
到
n=k+1
增加了哪些项或减少了哪些项
.
【
小题快练
】
链接教材 练一练
1.(
选修
2-2P99
习题
B
组
T1
改编
)
在应用数学归纳法证
明凸
n
边形的对角线为
n(n-3)
条时
,
第一步检验
n
等
于
(
)
A.1 B.2 C.3 D.4
【
解析
】
选
C.
三角形是边数最少的凸多边形
,
故第一步应检验
n=3.
2.(
选修
2-2P96
习题
2.3A
组
T1(3)
改编
)
用数学归纳法证明“
1+2+2
2
+…+2
n-1
=2
n
-1(n∈N
*
)”
的过程中
,
第二步
n=k
时等式成立
,
则当
n=k+1
时
,
应得到
(
)
A.1+2+2
2
+…+2
k-2
+2
k-1
=2
k+1
-1
B.1+2+2
2
+…+2
k
+2
k+1
=2
k
-1+2
k+1
C.1+2+2
2
+…+2
k-1
+2
k+1
=2
k+1
-1
D.1+2+2
2
+…+2
k-1
+2
k
=2
k+1
-1
【
解析
】
选
D.
由条件知
,
左边从
2
0
,2
1
到
2
n-1
都是连续的
,
因此当
n=k+1
时
,
左边应为
1+2+2
2
+…+2
k-1
+2
k
,
而右边应为
2
k+1
-1.
感悟专题 试一试
3.(2016·
延安模拟
)
利用数学归纳法证明不等式
1)
时
,
第一步
:
不等式的左边是
________.
【
解析
】
用数学归纳法证明不等式
(n∈N
*
且
n>1)
时
,
第一步
:
不等式的左边是
答案
:
考向一
利用数学归纳法证明等式
【
典例
1】
(2016·
宜春模拟
)
求证
(n∈N
*
).
【
解题导引
】
根据数学归纳法证明等式的步骤进行证明
.
【
规范解答
】
(1)
当
n=1
时
,
左边
=
右边
=
左边
=
右边
.
(2)
假设
n=k
时等式成立,
即
则当
n=k+1
时,
即当
n=k+1
时,等式也成立
.
综合
(1)(2)
可知,对一切
n∈N
*
,等式成立
.
【
规律方法
】
数学归纳法证明等式的思路和注意点
(1)
思路
:
用数学归纳法证明等式问题
,
要“先看项”
,
弄清等式两边的构成规律
,
等式两边各有多少项
,
初始值
n
0
是多少
.
(2)
注意点
:
由
n=k
时等式成立
,
推出
n=k+1
时等式成立
,
一要找出等式两边的变化
(
差异
),
明确变形目标
;
二要充分利用归纳假设
,
进行合理变形
,
正确写出证明过程
.
易错提醒
:
数学归纳法强调步骤“程式化”
,
要充分利用归纳假设
,
否则就不是数学归纳法
.
【
变式训练
】
设
f(n)= (n∈N
*
).
求证
:f(1)+f(2)+…+f(n-1)=n[f(n)-1](n≥2,n∈N
*
).
【
证明
】
(1)
当
n=2
时
,
左边
=f(1)=1,
右边
=
左边
=
右边
,
等式成立
.
(2)
假设
n=k(k≥2,k∈N
*
)
时
,
结论成立
,
即
f(1)+f(2)+…+f(k-1)=k[f(k)-1],
那么
,
当
n=k+1
时
,
f(1)+f(2)+…+f(k-1)+f(k)
=k[f(k)-1]+f(k)=(k+1)f(k)-k
=(k+1)f(k+1)-(k+1)=(k+1)[f(k+1)-1],
所以当
n=k+1
时结论仍然成立
.
综合
(1)(2)
可知
,
对一切
n≥2,n∈N
*
,
等式成立
.
【
加固训练
】
1.
用数学归纳法证明
:
对任意的
n∈N
*
,
【
证明
】
(1)
当
n=1
时
,
左边
=
右边
=
左边
=
右边
,
等式成立
.
(2)
假设当
n=k(k∈N
*
且
k≥1)
时等式成立
,
即有
则当
n=k+1
时
,
所以当
n=k+1
时
,
等式也成立
,
由
(1)(2)
可知
,
对一切
n∈N
*
等式都成立
.
2.
用数学归纳法证明
1+a+a
2
+…+a
n-1
= (a≠1,n∈N
*
).
【
证明
】
(1)
当
n=1
时
,
左边
=1,
右边
= =1,
等式成立
.
(2)
假设当
n=k(k∈N
*
)
时
,
等式成立
,
即
1+a+a
2
+…+a
k-1
=
那么
n=k+1
时
,
左边
=1+a+a
2
+…+a
k-1
+a
k
= +a
k
所以等式也成立
.
由
(1)(2)
可知
,
对任意
n∈N
*
等式均成立
.
考向二
利用数学归纳法证明不等式
【
典例
2】
已知数列
{a
n
},a
n
≥0,a
1
=0, a
n+1
2
+a
n+1
-1=a
n
2
.
求证
:
当
n∈N
*
时
,a
n
0,
又
a
k+1
>a
k
≥0,
所以
a
k+2
+a
k+1
+1>0,
所以
a
k+1
a
2
成立
.
(2)
假设当
n=k(k∈N
*
,k≥1)
时
,a
k+1
0,
又
a
k+2
+a
k+1
+1<-1+(-1)+1=-1,
所以
a
k+2
-a
k+1
<0,
所以
a
k+2
2),
对一切
n∈N
*
,a
n
>0,a
n+1
=
试证明
a
n
>2.
【
证明
】
当
n=1
时
,a
1
=a>2,
故命题
a
n
>2
成立
;
假设
n=k(k≥1
且
k∈N
*
)
时命题成立
,
即
a
k
>2,
那么
,
所以
a
k+1
>2,
即
n=k+1
时命题也成立
.
综上所述
,
命题
a
n
>2
对一切正整数都成立
.
【
规律方法
】
应用数学归纳法证明不等式的适用范围及关键
(1)
适用范围
:
当遇到与正整数
n
有关的不等式证明时
,
应用其他办法不容易证
,
则可考虑应用数学归纳法
.
(2)
关键
:
用数学归纳法证明不等式的关键是由
n=k
成立
,
推证
n=k+1
时也成立
,
证明时用上归纳假设后
,
可采用分析法、综合法、求差
(
求商
)
比较法、放缩法等证明
.
【
变式训练
】
(2014·
安徽高考改编
)
设整数
p>1.
证明
:
当
x>-1
且
x≠0
时
,(1+x)
p
>1+px.
【
证明
】
①
当
p=2
时
,(1+x)
2
=1+2x+x
2
>1+2x,
原不等式成立
.
②假设当
p=k(k≥2,k∈N
*
)
时
,
不等式
(1+x)
k
>1+kx
成立
.
则当
p=k+1
时
,(1+x)
k+1
=(1+x)(1+x)
k
>(1+x)
·
(1+kx)
=1+(k+1)x+kx
2
>1+(k+1)x.
所以当
p=k+1
时
,
原不等式也成立
.
综合①②可得
,
当
x>-1
且
x≠0
时
,
对一切整数
p>1,
不等式
(1+x)
p
>1+px
均成立
.
【
加固训练
】
1.
等比数列
{a
n
}
的前
n
项和为
S
n
,
已知对任意的
n∈N
*
,
点
(n,S
n
)
均在函数
y=b
x
+r(b
>0
且
b≠1,b,r
均为常数
)
的图
象上
.
(1)
求
r
的值
.
(2)
当
b=2
时
,
记
b
n
=2(log
2
a
n
+1)(n∈N
*
),
证明
:
对任意的
n∈N
*
,
不等式 成立
.
【
解析
】
(1)
由题意
,S
n
=b
n
+r
,
当
n≥2
时
,S
n-1
=b
n-1
+r.
所以
a
n
=S
n
-S
n-1
=b
n-1
(b-1),
由于
b>0
且
b≠1,
所以
n≥2
时
,{a
n
}
是以
b
为公比的等比数列
,
又
a
1
=b+r,a
2
=b(b-1),
故
=b,
即 解得
r=-1.
(2)
由
(1)
知
a
n
=2
n-1
,
因此
b
n
=2n(n∈N
*
),
所证不等式为
①当
n=1
时
,
左边
= ,
右边
= ,
左边
>
右边
,
所以结论成
立
.
②假设
n=k(k≥1,k∈N
*
)
时结论成立
,
即
则当
n=k+1
时
,
要证当
n=k+1
时结论成立
,
只需证
即证
由均值不等式 成立
,
故 成立
,
所以
,
当
n=k+1
时
,
结论成立
.
由①②可知
n∈N
*
时
,
不等式
成立
.
2.
设
n∈N
*
,n>1,
求证
:
【
证明
】
(
用数学归纳法证明
)
(1)
当
n=2
时
,
不等式左边
= =
右边
.
(2)
假设
n=k(k
>1,k∈N
*
)
时
,
不等式成立
,
即
那么当
n=k+1
时
,
有
所以当
n=k+1
时
,
不等式也成立
.
由
(1)(2)
可知对任何
n∈N
*
,n>1,
均成立
.
3.
若不等式 对一切正整数
n
都成立
,
求正整数
a
的最大值
,
并证明结论
.
【
解析
】
当
n=1
时
,
即 所以
a<26.
而
a
是正整数
,
所以取
a=25,
下面用数学归纳法证明
(1)
当
n=1
时
,
已证得不等式成立
.
(2)
假设当
n=k(k∈N
*
)
时
,
不等式成立
,
即
则当
n=k+1
时
,
有
因为
所以当
n=k+1
时不等式也成立
.
由
(1)(2)
知
,
对一切正整数
n,
都有
所以
a
的最大值等于
25.
4.
已知
f(n)= g(n)= n∈N
*
.
(1)
当
n=1,2,3
时
,
试比较
f(n
)
与
g(n
)
的大小
.
(2)
猜想
f(n
)
与
g(n
)
的大小关系
,
并给出证明
.
【
解析
】
(1)
当
n=1
时
,f(1)=1,g(1)=1,
所以
f(1)=g(1);
当
n=2
时
,f(2)= ,g(2)= ,
所以
f(2)2
3
-1,
由此猜想
:a
n
≥2
n
-1.
下面用数学归纳法证明这个猜想
:
①
当
n=1
时
,a
1
≥2
1
-1=1,
结论成立
;
②
假设
n=k(k≥1
且
k∈N
*
)
时结论成立
,
即
a
k
≥2
k
-1.
当
n=k+1
时
,
由
g(x
)=(x+1)
2
-1
在区间
[1,+∞)
上单调递增知
a
k+1
≥(a
k
+1)
2
-1≥2
2k
-1≥2
k+1
-1,
即
n=k+1
时
,
结论也成立
.
由①②知
,
对任意
n∈N
*
,
都有
a
n
≥2
n
-1.
即
1+a
n
≥2
n
,
所以
所以
命题方向
2:
与数列有关的证明题
【
典例
4】
(2014·
广东高考
)
设数列
{a
n
}
的前
n
项和为
S
n
,
满足
S
n
=2na
n+1
-3n
2
-4n,n∈N
*
,
且
S
3
=15.
(1)
求
a
1
,a
2
,a
3
的值
.
(2)
求数列
{a
n
}
的通项公式
.
【
解题导引
】
(1)
取
n=1,n=2,
结合
S
3
=15
列方程组求
a
1
,a
2
,a
3
.
(2)
利用
a
n
=S
n
-S
n-1
(n≥2),
先猜出
a
n
,
再用数学归纳法给出证明
.
【
规范解答
】
(1)
由已知得
解得
a
1
=3,a
2
=5,a
3
=7.
(2)
猜测
a
n
=2n+1.
由
S
n
=2na
n+1
-3n
2
-4n
得
S
n-1
=2(n-1)a
n
-3(n-1)
2
-4(n-1)(n≥2),
当
n≥2
时
,a
n
=S
n
-S
n-1
,
所以两式相减
,
整理得
a
n
=2na
n+1
-2(n-1)a
n
-6n-1,
又
a
2
=5,a
1
=3,
满足式子
,
建立了
a
n
与
a
n+1
的递推关系
(n∈N
*
);
因为当
n=1
时
,a
1
=3,
假设
a
k
=2k+1
成立
,
那么
n=k+1
时
,
综上对于
n∈N
*
,
有
a
n
=2n+1,
所以数列
{a
n
}
的通项公式为
a
n
=2n+1.
【
技法感悟
】
1.“
归纳
——
猜想
——
证明”的一般步骤
(1)
计算
(
根据条件
,
计算若干项
).
(2)
归纳猜想
(
通过观察、分析、综合、联想
,
猜想出一般结论
).
(3)
证明
(
用数学归纳法证明
).
2.
与“归纳
——
猜想
——
证明”相关的常用题型的处理策略
(1)
与函数有关的证明题
:
由已知条件验证前几个特殊值正确得出猜想
,
充分利用函数的有关性质及数学归纳法证明
.
(2)
与数列有关的证明题
:
利用已知条件
,
当直接证明遇阻时
,
可考虑应用数学归纳法并结合数列的概念、判定及性质进行证明
.
【
题组通关
】
1.(2016·
上饶模拟
)
已知等差数列
{a
n
}
的公差
d
大于
0,
且
a
2
,a
5
是方程
x
2
-12x+27=0
的两根
,
数列
{b
n
}
的前
n
项和
为
T
n
且
T
n
=1- b
n
.
(1)
求数列
{a
n
},{b
n
}
的通项公式
.
(2)
设数列
{a
n
}
的前
n
项和为
S
n
,
试比较 与
S
n+1
的大小
,
并说明理由
.
【
解析
】
(1)
由已知得
又因为
{a
n
}
的公差大于
0,
所以
a
5
>a
2
,
所以
a
2
=3,a
5
=9,
所以
d= =2,a
1
=1,
因为
T
n
=1- b
n
,b
1
= ,
当
n≥2
时
,T
n-1
=1- b
n-1
,
因为
b
n
=T
n
-T
n-1
=
化简
,
得
b
n
= b
n-1
,
所以
{b
n
}
是首项为
,
公比为 的等比数列
,
即
所以
a
n
=2n-1,b
n
= .
(2)
因为
所以
S
n+1
=(n+1)
2
,
以下比较 与
S
n+1
的大小
:
当
n=1
时
, S
2
=4,
所以
S
5
,
猜想
:n≥4
时
, >S
n+1
.
下面用数学归纳法证明
:
①
当
n=4
时
,
已证
.
②
假设当
n=k(k∈N
*
,k≥4)
时
, >S
k+1
,
即
>(k+1)
2
,
那么
,n=k+1
时
,
=3k
2
+6k+3=(k
2
+4k+4)+2k
2
+2k-1>[(k+1)+1]
2
=S
(k+1)+1
.
综合①②
,
当
n≥4
时
, >S
n+1
.
2.(2014·
重庆高考
)
设
a
1
=1,a
n+1
= +b(n∈N
*
).
(1)
若
b=1,
求
a
2
,a
3
及数列
{a
n
}
的通项公式
.
(2)
若
b=-1,
问
:
是否存在实数
c
使得
a
2n
f(a
2k+1
)>f(1)=a
2
,
即
1>c>a
2k+2
>a
2
.
再由
f(x
)
在
(
-∞,1]
上为减函数得
c=
f(c
)
查看更多