宁夏石嘴山市第三中学2020届高三高考第五次模拟考试数学（文）试题

宁夏石嘴山市第三中学2020届高三高考第五次模拟考试数学（文）试题

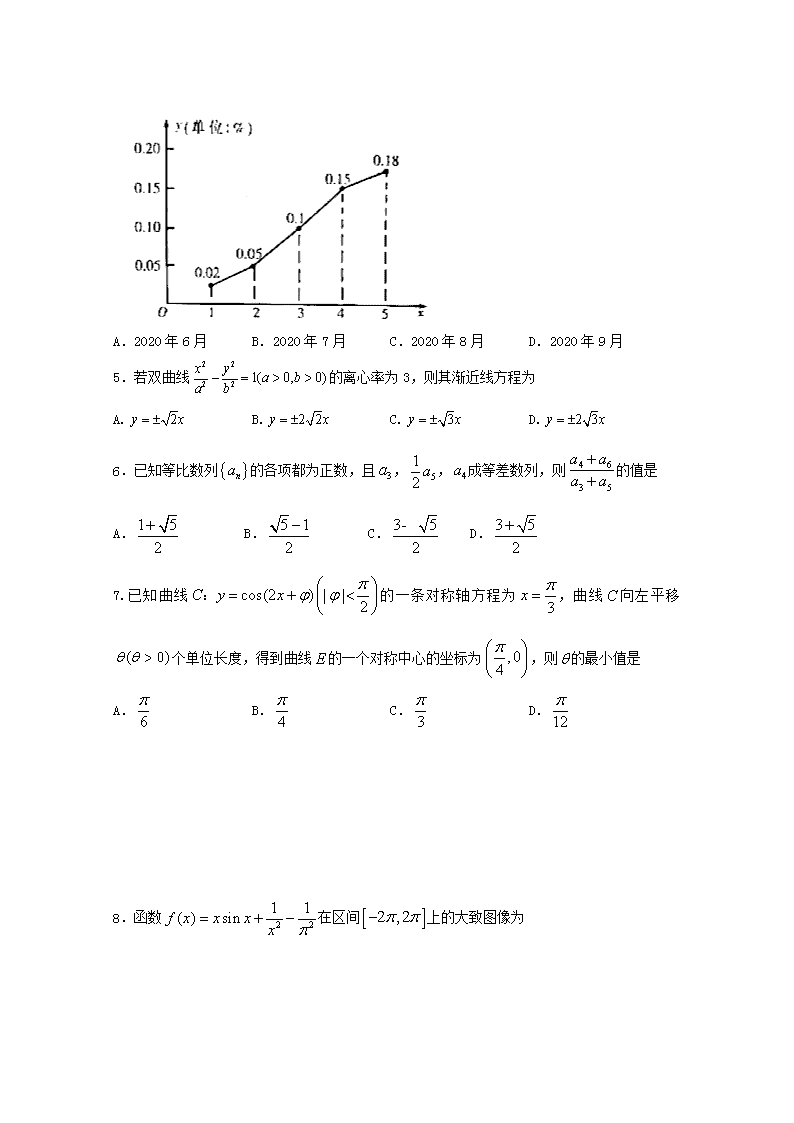
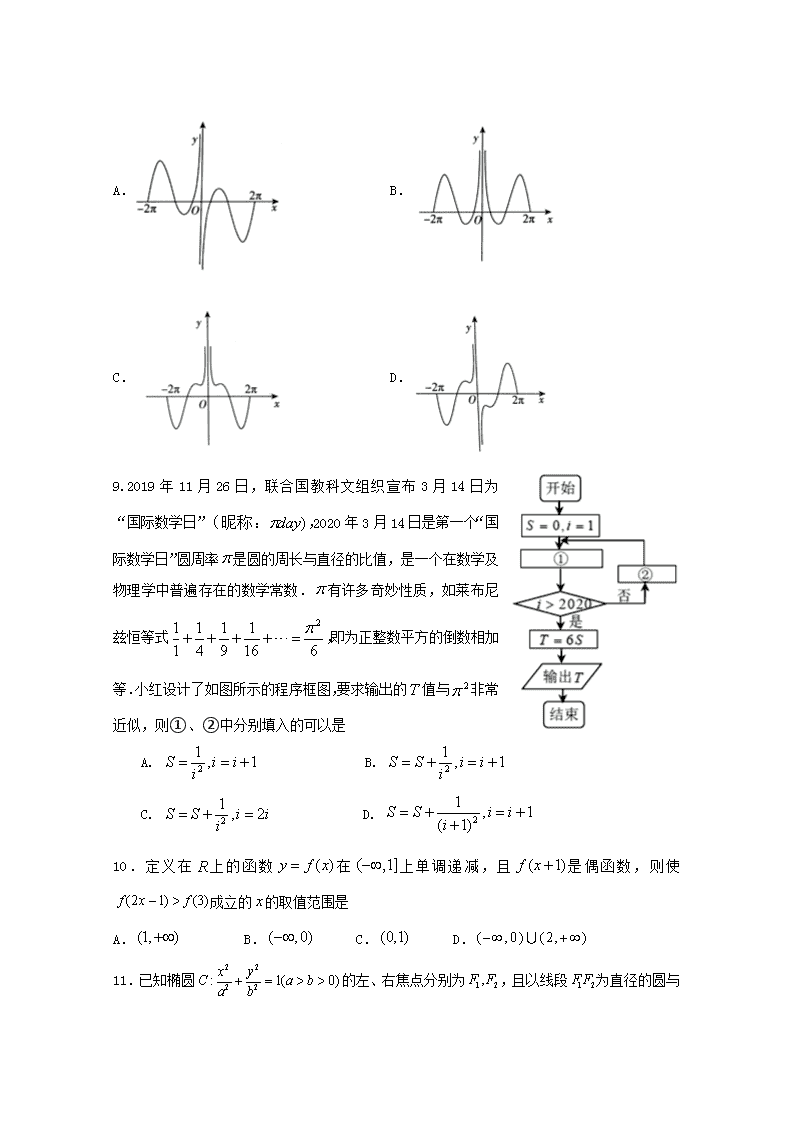
‎ 石嘴山三中2020届第五次模拟考试 ‎（文科）数学试卷 注意事项：‎ ‎1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在考生信息条形码粘贴区。‎ ‎2．选择题必须使用2B铅笔填涂；非选择题必须使用0.5毫米黑色字迹的签字笔书写，字体工整、笔迹清楚。‎ ‎3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效。‎ ‎4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。‎ ‎ ‎ 一、选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的．‎ ‎1.已知集合，，则集合中元素的个数为 A.2 B‎.3 ‎C.4 D.5‎ ‎2．若复数为纯虚数，则 A． B． C． D．‎ ‎3．已知向量 ， ，若 ，则实数 A. B. ‎1 ‎C. 2 D. ‎ ‎4．网络是一种先进的高频传输技术，我国的技术发展迅速，已位居世界前列.华为公司2019年8月初推出了一款手机，现调查得到该款手机上市时间和市场占有率（单位：%）的几组相关对应数据.如图所示的折线图中，横轴1代表2019年8月，2代表2019年9月……，5代表2019年12月，根据数据得出关于的线性回归方程为.若用此方程分析并预测该款手机市场占有率的变化趋势，则最早何时该款手机市场占有率能超过0.5%（精确到月）‎ A．2020年6月 B．2020年7月 C．2020年8月 D．2020年9月 ‎5．若双曲线的离心率为3，则其渐近线方程为 A. B. C. D.‎ ‎6．已知等比数列的各项都为正数，且，，成等差数列，则的值是 A． B． C． D．‎ ‎7.已知曲线的一条对称轴方程为，曲线向左平移个单位长度，得到曲线的一个对称中心的坐标为，则的最小值是 A． B． C． D．‎ ‎8．函数在区间上的大致图像为 A． B．‎ C． D．‎ ‎9.‎2019年11月26日，联合国教科文组织宣布‎3月14日为“国际数学日”，‎2020年3月14日是第一个“国际数学日”圆周率是圆的周长与直径的比值，是一个在数学及物理学中普遍存在的数学常数．有许多奇妙性质，如莱布尼兹恒等式，即为正整数平方的倒数相加等．小红设计了如图所示的程序框图，要求输出的值与非常近似，则①、②中分别填入的可以是 A. B. C. D. ‎ ‎10．定义在上的函数在上单调递减，且是偶函数，则使成立的的取值范围是 A． B． C． D．‎ ‎11．已知椭圆的左、右焦点分别为，且以线段 为直径的圆与直线相切，则的离心率为 A． B． C． D．‎ ‎12．如图，在边长为4的正三角形中，为边的中点，过作于．把沿翻折至的位置，连结．翻折过程中，有下列三个结论：‎ ‎①；②存在某个位置，使；‎ ‎③若，则的长是定值．其中所有正确结论的编号是 A．①② B．①③ C．②③ D．①②③‎ 二、填空题（本大题共4小题，共20分）‎ ‎13.设数列满足，，则__________．‎ ‎14.已知函数，则=________．‎ ‎15．某几何体的三视图如图所示，网格纸上小正方形的边长为1，则该几何体的表面积为________．‎ 16． 已知直线与圆相交于两点（为圆心），且为等腰直角三角形，则实数的值为________.‎ 三、解答题：（本大题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤）‎ ‎17．（本小题满分12分） ‎ 在中，.‎ (1) 求的值；‎ (2) 若，求的面积.‎ 18． ‎（本小题满分12分）‎ 已知正三棱柱中，，是的中点.‎ ‎（1）求证：平面；‎ ‎（2）求三棱锥的体积.‎ ‎19 （本小题满分12分）‎ 为了打好脱贫攻坚战，某贫困县农科院针对玉米种植情况进行调研，力争有效地改良玉米品种，为农民提供技术支援，现对已选出的一组玉米的茎高进行统计，获得茎叶图如图单位：厘米，设茎高大于或等于‎180厘米的玉米为高茎玉米，否则为矮茎玉米． （1） 求出易倒伏玉米茎高的中位数m； （2） 根据茎叶图的数据，完成下面的列联表：‎ 抗倒伏 易倒伏 矮茎 高茎 (1) 根据(2)中的列联表，是否可以在犯错误的概率不超过1％的前提下，认为抗倒伏与玉米矮茎有关？ 附：，‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ K ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎20.（本小题满分12分） ‎ 已知是抛物线：的焦点，点在抛物线上，且．‎ ‎(1) 求抛物线的标准方程；‎ ‎(2) 若是抛物线上的两个动点，且，为坐标原点，‎ 求证：直线过定点．‎ ‎21.（本小题满分12分） ‎ 已知函数． （1） 讨论函数的单调性； （2） 若函数图象过点，求证：．‎ 请考生在22，23，题中任选一题作答，如果多做，则按所做的第一题记分．做答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．‎ ‎22.[选修4-4：坐标系与参数方程]‎ 在直角坐标系中，以原点为极点，以轴的正半轴为极轴，曲线的极坐标方程为.‎ ‎（1）将曲线的极坐标方程化为直角坐标方程；‎ ‎（2）过点作倾斜角为的直线l与圆交于两点，试求的值．‎ ‎23.[选修4—5：不等式选讲] ‎ 设函数.‎ ‎（1）若，解不等式；‎ ‎（2）若函数有最小值，求实数的取值范围.‎ 石嘴山三中2020届第五次模拟考试 ‎（文科）数学试卷 一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.请把正确选项涂在答题卡的相应位置上．）‎ 题目 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 C A B C B A C C B D D B 二、填空题(本大题共4小题，每小题5分,共20分.)‎ ‎13. ________ 14. ___________‎ ‎15. ____ ___． 16. ‎ 三、解答题（本大题共7小题，共70分）‎ ‎17．（本小题满分12分） ‎ 在中，.‎ (1) 求的值；‎ (2) 若，求的面积.‎ ‎17.答案：(1)在中，因为，，‎ 所以由正弦定理得.‎ ‎(2)因为，所以.‎ 由余弦定理 得，得或（舍）.‎ 的面积 18． ‎（本小题满分12分）‎ 已知正三棱柱中，，是的中点.‎ （1) 求证：平面；‎ ‎（2）求三棱锥的体积.‎ ‎【详解】证明：（1）连结，设，再连接,如图，‎ 则是的中点，是的中位线，所以∥，‎ 又因为平面，平面，所以∥平面 ‎（2）过点作，垂足为，如图，‎ 在正三棱柱中，平面，∴，又∵，‎ ‎∴平面，，‎ ‎∴.‎ ‎19 （本小题满分12分）‎ 为了打好脱贫攻坚战，某贫困县农科院针对玉米种植情况进行调研，力争有效地改良玉米品种，为农民提供技术支援，现对已选出的一组玉米的茎高进行统计，获得茎叶图如图单位：厘米，设茎高大于或等于‎180厘米的玉米为高茎玉米，否则为矮茎玉米． （1） 求出易倒伏玉米茎高的中位数m； （2） 根据茎叶图的数据，完成下面的列联表：‎ 抗倒伏 易倒伏 矮茎 高茎 (1) 根据(2)中的列联表，是否可以在犯错误的概率不超过1％的前提下，认为抗倒伏与玉米矮茎有关？ 附：，‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ K ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎【答案】解：； ‎ 抗倒伏 易倒伏 矮茎 ‎15‎ ‎4‎ 高茎 ‎10‎ ‎16‎ 由于， 因此可以在犯错误的概率不超过的前提下，认为抗倒伏与玉米矮茎有关．‎ ‎【解析】根据茎叶图可求易倒伏玉米茎高的中位数； 根据茎叶图的数据，即可完成列联表： 计算K的观测值，对照题目中的表格，得出统计结论． 本题主要考查了中位数的求法，考查了独立性检验的应用问题，也考查了计算能力的应用问题，是基础题目． ‎ ‎20.已知是抛物线：的焦点，点在抛物线上，且．‎ ‎(1) 求抛物线的标准方程；‎ ‎(2) 若是抛物线上的两个动点，且，为坐标原点，‎ 求证：直线过定点．‎ ‎【答案】Ⅰ由题意得，，解得， 因为点在抛物线C上， 则，解得， 又，所以， 即得抛物线C的标准方程为． Ⅱ设，， 因为，所以， 即得， 因为点A、B在抛物线C上， 所以，，代入得， 因为，则 ‎， 设直线AB的方程为，联立 得，， 则，所以，满足， 所以直线AB的方程为，过定点．‎ ‎21.已知函数． （1） 讨论函数的单调性； （2） 若函数图象过点，求证：．‎ ‎【答案】解：Ⅰ函数的定义域为，． 当时，，在上单调递增； 当时，由，得． 若，，单调递增； 若，，单调递减 综合上述：当时，在上单调递增； 当时，在单调递增，在上单调递减． Ⅱ证明：函数图象过点， ，解得． 即， 令， ． 令，， 函数在上单调递增， 存在，使得，可得，． ‎ ‎． 成立．‎ 请考生在22，23，题中任选一题作答，如果多做，则按所做的第一题记分．做答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．‎ ‎22.[选修4-4：坐标系与参数方程]‎ 在直角坐标系中，以原点为极点，以轴的正半轴为极轴，曲线的极坐标方程为.‎ ‎（1）将曲线的极坐标方程化为直角坐标方程；‎ ‎（2）过点作倾斜角为的直线l与圆交于两点，试求的值．‎ ‎22.答案：（1）将曲线的极坐标方程，化为直角坐标方程为：；‎ ‎（2）直线l的参数方程为：（t为参数），将其带入上述方程中得：，则，所以 ‎23.[选修4—5：不等式选讲] ‎ 设函数.‎ ‎（1）若，解不等式；‎ ‎（2）若函数有最小值，求实数的取值范围.‎ ‎23．（10分）‎ ‎23.答案：(1) 时， ‎ 综上，得 综上，原不等式的解集为 ‎(2) ‎ 函数有最小值，则