高中数学必修5：4_备课资料（3_3_1　二元一次不等式(组)与平面区域）

高中数学必修5：4_备课资料（3_3_1　二元一次不等式(组)与平面区域）

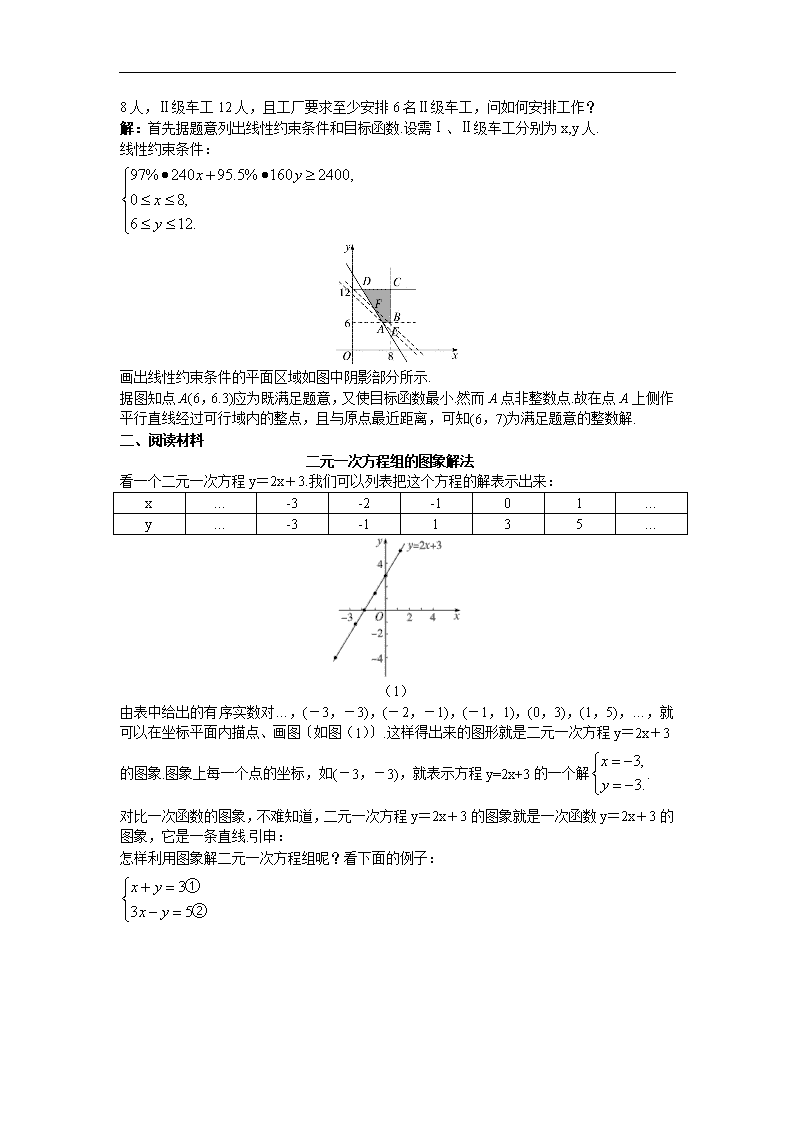
备课资料 一、备用例题 ‎【例1】 设实数x、y满足不等式组求点(x,y)所在的平面区域. 分析:必须使学生明确，求点(x,y)所在的平面区域，关键是确定区域的边界线.可以从去掉绝对值符号入手. 解：已知的不等式组等价于或. 解得点(x,y)所在平面区域为下图所示的阴影部分(含边界).其中AB：y=2x-5;BC:x+y=4;CD:y=-2x+1;DA:x+y=1. ‎【例2】 某工厂要安排一种产品生产，该产品有Ⅰ、Ⅱ、Ⅲ三种型号，生产这种产品需要两种主要资源：原材料和劳动力，每件产品所需资源数量以及每件产品出售价格如下表所示：‎ ‎ 型号 货源 Ⅰ Ⅱ Ⅲ 原材料(千克/件)‎ 劳动力(小时/件)‎ ‎4‎ ‎3‎ ‎6‎ ‎2‎ ‎4‎ ‎5‎ 每天可利用的原材料为120千克，劳动力为100小时，假定该产品只要生产出来即可销售出去，试确定三种型号产品的日产量，使总产值最大. 分析:建立数学模型： ‎(1)用x 1、x 2、x 3分别表示Ⅰ、Ⅱ、Ⅲ三种型号的日产量. ‎(2)明确约束条件：‎ 这样，这个资源利用问题的数学模型为满足约束条件的可行域.‎ ‎【例3】 某机械厂的车工分Ⅰ、Ⅱ两个等级，各级车工每人每天加工能力，成品合格率如下表所示：‎ 级别 加工能力(个/人天)‎ 成品合格率(%)‎ Ⅰ ‎240‎ ‎97‎ Ⅱ ‎160‎ ‎95.5‎ 工厂要求每天至少加工配件2 400个，车工每出一个废品，工厂要损失2元，现有Ⅰ级车工 ‎8人，Ⅱ级车工12人，且工厂要求至少安排6名Ⅱ级车工，问如何安排工作？ 解：首先据题意列出线性约束条件和目标函数.设需Ⅰ、Ⅱ级车工分别为x,y人. 线性约束条件： 画出线性约束条件的平面区域如图中阴影部分所示. 据图知点A(6，6.3)应为既满足题意，又使目标函数最小.然而A点非整数点.故在点A上侧作平行直线经过可行域内的整点，且与原点最近距离，可知(6，7)为满足题意的整数解. 二、阅读材料 二元一次方程组的图象解法 看一个二元一次方程y＝2x＋3.我们可以列表把这个方程的解表示出来： x ‎…‎ ‎-3‎ ‎-2‎ ‎-1‎ ‎0‎ ‎1‎ ‎…‎ y ‎…‎ ‎-3‎ ‎-1‎ ‎1‎ ‎3‎ ‎5‎ ‎…‎ ‎（1）‎ 由表中给出的有序实数对…，(－3，－3)，(－2，－1)，(－1，1)，(0，3)，(1，5)，…，就可以在坐标平面内描点、画图〔如图（1）〕.这样得出来的图形就是二元一次方程y＝2x＋3的图象.图象上每一个点的坐标，如(－3，－3)，就表示方程y=2x+3的一个解. 对比一次函数的图象，不难知道，二元一次方程y＝2x＋3的图象就是一次函数y＝2x＋3的图象，它是一条直线.引申： 怎样利用图象解二元一次方程组呢？看下面的例子： ‎（2）‎ 先在同一直角坐标系内分别画出这两个二元一次方程的图象〔如图（2）〕. 由方程①，有 过点(0，3)与(3，0)画出直线x＋y＝3. 由方程②，有 过点(0，－5)与(，0)画出直线3x－y＝5. 两条直线有一个交点，交点的坐标就表示两个方程的公共解，交点坐标是(2，1)，所以原方程组的解是 这与用代入法或加减法解得的结果相同.提问 在解二元一次方程组时，会遇到其中一个方程是x＝3或y＝2这种形式. x＝3或y＝2的图象是怎样的呢？ 方程x＝3可以看成x＋0·y＝3， 它的解列出表来是 x ‎…‎ ‎3‎ ‎3‎ ‎3‎ ‎3‎ ‎…‎ y ‎…‎ ‎-1‎ ‎0‎ ‎1‎ ‎2‎ ‎…‎ 可以看到，无论y取什么数值，x的值都是3，所有表示方程x＝3的解的点组成一条直线，这条直线过点(3，0)，且平行于y轴.这条直线就是方程x＝3的图象，我们把它叫做直线x＝3〔如图(3)〕. 同样，方程y＝2的图象是过点(0，2)，且平行于x轴的一条直线，叫做直线y＝2〔如图(3)〕. ‎(3)‎