第13章 不等式选讲 检测A卷-2020年领军高考数学一轮复习（文理通用） Word版含解析

第13章 不等式选讲 检测A卷-2020年领军高考数学一轮复习（文理通用） Word版含解析

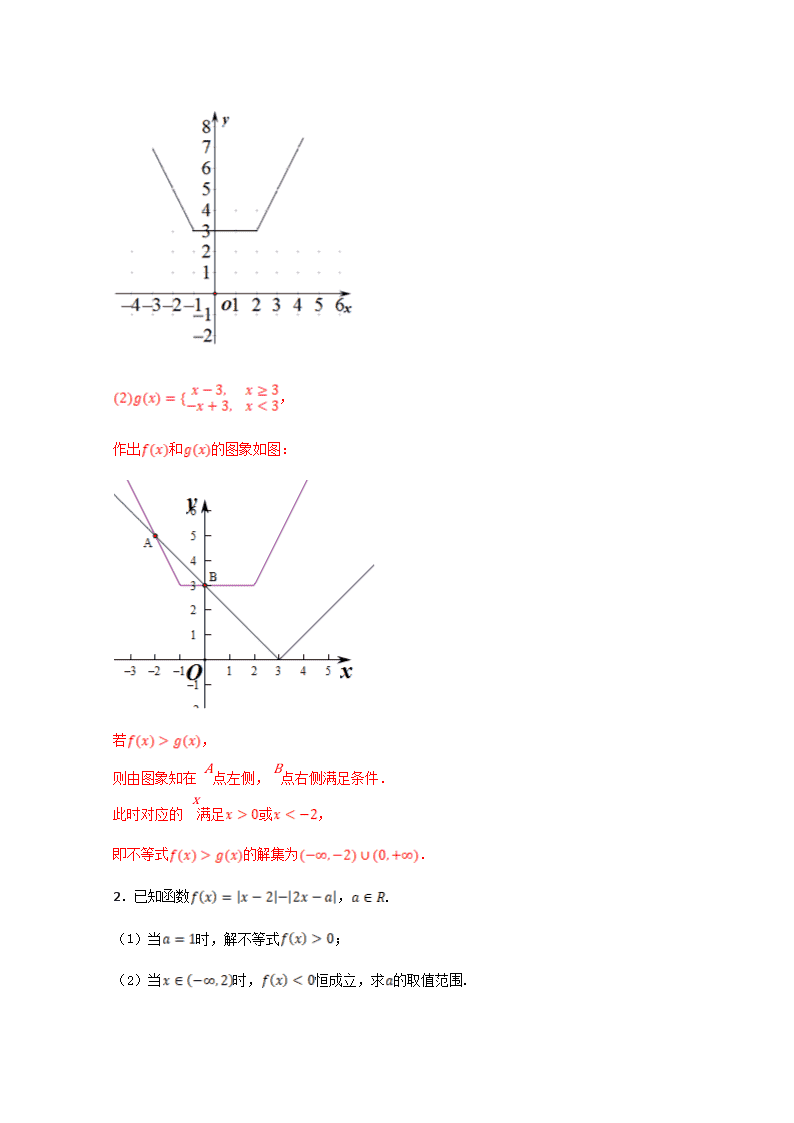
‎2020年领军高考数学一轮复习(文理通用)‎ 选修系列—不等式选讲 章节验收测试卷A卷 姓名 班级 准考证号 ‎ ‎ 1．已知函数，．‎ 在答题卡中的平面直角坐标系里作出的图象；‎ 求满足的x的取值范围．‎ ‎【答案】（1）详见解析；（2）详见解析.‎ ‎【解析】‎ ‎(1)f(x)=|x+1|+|x-2|，，‎ 则对应的图象如图：‎ ‎，‎ 作出和的图象如图：‎ 若，‎ 则由图象知在A点左侧，B点右侧满足条件．‎ 此时对应的x满足或，‎ 即不等式的解集为． 2．已知函数，.‎ ‎（1）当时，解不等式；‎ ‎（2）当时，恒成立，求的取值范围.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎（1）当时，即 等价于：，或，或 解得或或 所以原不等式的解集为：.‎ ‎（2）所以可化为 即或 ‎①式恒成立等价于或 ‎∵，∴或，‎ ‎∴. 3．（1）已知都是正数，并且，求证：；‎ ‎（2）已知，求证．‎ ‎【答案】（1）见解析；（2）见解析.‎ ‎【解析】‎ ‎（1）‎ ‎.‎ ‎∵都是正数,∴,又∵,∴,‎ ‎∴,∴；‎ ‎（2）∵，∴，即，要证，‎ 只需证，只需要证，‎ 而，∴显然成立，于是命题得证.（或用作差法） 4．已知 ‎（1）解不等式；‎ ‎（2）作出函数的图象，若恒成立，求的取值范围.‎ ‎【答案】(1）(2)‎ ‎【解析】‎ ‎（1），不等式可化为：或或，解得：或或，综上：‎ ‎（2）作出的图像如下图：‎ 要使得恒成立，则，即： 5．选修4-5：不等式选讲：设函数.‎ ‎（1）求不等式的解集；‎ ‎（2）若对任意恒成立，求的取值范围.‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎（1）因为 ，‎ 所以等价于或或，‎ 解得或或，所以不等式的解集为.‎ ‎（2）对恒成立，‎ 即即可，‎ 因为 ，‎ 所以，即，‎ 解得. 6．已知函数．‎ ‎（1）解不等式；‎ ‎（2）若对恒成立，求实数的取值范围．‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎（1）由题知不等式，‎ 即，‎ 等价于，‎ 或，‎ 或；‎ 解得或或，即或，‎ 原不等式的解集为，，；‎ ‎（2）由题知，‎ 的最小值为3，‎ ‎，‎ 解得，‎ 实数的取值范围为，． 7．已知函数，其中.‎ ‎（1）当时，求不等式的解集；‎ ‎（2）若存在，使得，求实数的取值范围.‎ ‎【答案】（1）或（2）‎ ‎【解析】‎ ‎（1）当时，，‎ 所以或或，‎ 解得或，‎ 因此不等式的解集的或 ‎（2） ，易知 ‎，由题意，知，，解得，‎ 所以实数的取值范围是 8．（1）已知，且，求证：；‎ ‎（2）解关于的不等式：．‎ ‎【答案】（1）见解析； （2）见解析 ‎【解析】‎ ‎（1）∵a+b+c=1，代入不等式的左端，∴==‎ ‎=‎ ‎=．‎ ‎∵a，b，c∈（0，+∞），∴．‎ ‎∴．‎ ‎∴（当且仅当时，等号成立）．‎ ‎（2）原不等式可化为ax2+（a﹣2）x﹣2≥0，化简为（x+1）（ax﹣2）≥0．‎ ‎∵a＜0，∴．‎ ‎1°当﹣2＜a＜0时，；‎ ‎2°当a=﹣2时，x=﹣1；‎ ‎3°当a＜﹣2时，．‎ 综上所述，当﹣2＜a＜0时，解集为；‎ 当a=﹣2时，解集为{x|x=﹣1}；‎ 当a＜﹣2时，解集为． 9．已知函数．‎ 若的最小值为5，求实数a的值；‎ 当时，不等式恒成立，求实数a的取值范围．‎ ‎【答案】（1）或；（2）.‎ ‎【解析】‎ ‎，‎ 当且仅当时取等号，‎ ‎，‎ 由，解得：或；‎ 原命题等价于在恒成立，‎ 即在恒成立，‎ 即在恒成立，‎ 即，‎ 故． 10．设函数.‎ ‎(1)求不等式的解集；‎ ‎(2)若存在使不等式成立，求实数的取值范围 ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎(1)由得，‎ ‎∴‎ ‎∴不等式的解集为 ‎ ‎(2)令 则，∴ ‎ ‎∵存在x使不等式成立，∴ 11．设函数，求的最小值；‎ ‎【答案】3‎ ‎【解析】‎ 因为 ，‎ 又因为当时；当时；当时，‎ 所以的最小值为3. 12．已知函数．‎ ‎（1）解不等式；‎ ‎（2）若不等式对任意的恒成立，求实数的取值范围．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ ‎（1）由，‎ 得或或 解得或或，‎ 所以原不等式的解集为．‎ ‎（2）由不等式性质可知， ，‎ 若不等式对任意的恒成立，则，阶段，所以实数的取值范围为． 13．已知函数．‎ ‎（1）当时，解不等式；‎ ‎（2）若存在满足，求实数a的取值范围．‎ ‎【答案】（1）或；（2）‎ ‎【解析】‎ 当时，，‎ 当时，不等式等价于，解得，即；‎ 当时，不等式等价于，解得，即；‎ 当时，不等式等价于，解得，即．‎ 综上所述，原不等式的解集为或．‎ 由，即，‎ 得，‎ 又，‎ ‎，即，‎ 解得．所以。 14．设函数.‎ ‎（1）解不等式；‎ ‎（2）求函数的最大值.‎ ‎【答案】（1）；（2）3‎ ‎【解析】‎ ‎⑴①当x＜-1时，；‎ ‎②当-1≤x≤2时，，；‎ ‎③当时，，；‎ 综上，不等式的解集为； ‎ ‎⑵，由其图知，. 15．已知．‎ ‎（1）证明：；‎ ‎（2）若，求实数的取值范围．‎ ‎【答案】（1）证明见解析；（2）．‎ ‎【解析】‎ ‎（1）证明： ． ‎ ‎（2）解：若，则， ‎ 故 ‎∴或 ，‎ 解得：．‎ ‎∴实数的取值范围为． 16．设函数的定义域为.‎ ‎（1）求集合；‎ ‎（2）设，证明.‎ ‎【答案】（1）（2）见解析 ‎【解析】‎ ‎（1）解：，‎ 当时，，解得，‎ 当时，恒成立，‎ 当时，，解得，‎ 综上定义域.‎ ‎（2）证明，原不等式 由得，原不等式得证. 17．设函数 ‎ ‎（1）解不等式；‎ ‎（2）若存在不等式成立，求实数的取值范围．‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎（1）∵‎ ‎ ‎ ‎ ‎ ‎ ‎ 综上，不等式的解集为： ‎ ‎（2）存在使不等式成立 ‎ 由（Ⅰ）知，时，‎ 时， ‎ ‎ ‎ ‎∴实数的取值范围为 18．设函数f（x）=|2x+3|+|x﹣1|．‎ ‎（Ⅰ）解不等式f（x）＞4；‎ ‎（Ⅱ）若存在使不等式a+1＞f（x）成立，求实数a的取值范围．‎ ‎【答案】（Ⅰ）（Ⅱ）‎ ‎【解析】‎ ‎（Ⅰ）∵‎ ‎ ‎ ‎ ‎ ‎ ‎ 综上，不等式的解集为： ‎ ‎（Ⅱ）存在使不等式成立 ‎ 由（Ⅰ）知，时，‎ 时， ‎ ‎ ‎ ‎∴实数的取值范围为 19．已知函数，函数．当时，．‎ ‎（Ⅰ）证明：当时，；‎ ‎（Ⅱ）设，当时，的最大值等于．求．‎ ‎【答案】(Ⅰ)答案见解析；(Ⅱ).‎ ‎【解析】‎ ‎（Ⅰ）证明：由题意得：即 所以，‎ ‎.‎ 由于，‎ 所以当时，的最大值是或.‎ 所以.‎ ‎（Ⅱ）由题意得，‎ 又因为，且 所以或 解得或（舍去）.‎ 又因为当时，，且，‎ 所以.‎ 故.‎ 即.‎ 经检验，符合题意. 20．已知函数.‎ ‎（Ⅰ）若不等式的解集为，求的值； ‎ ‎（Ⅱ）若不等式的解集非空，求实数的取值范围.‎ ‎【答案】(Ⅰ)，；(Ⅱ).‎ ‎【解析】‎ ‎（Ⅰ）不等式成立，当且仅当与同时成立.‎ 依题意解得，.‎ ‎（Ⅱ）由绝对值三角不等式得的最小值是，‎ 所以不等式的解集非空，当且仅当满足，‎ 即.‎