- 2021-07-01 发布 |
- 37.5 KB |
- 27页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2019届二轮复习函数的应用课件(27张)(全国通用)
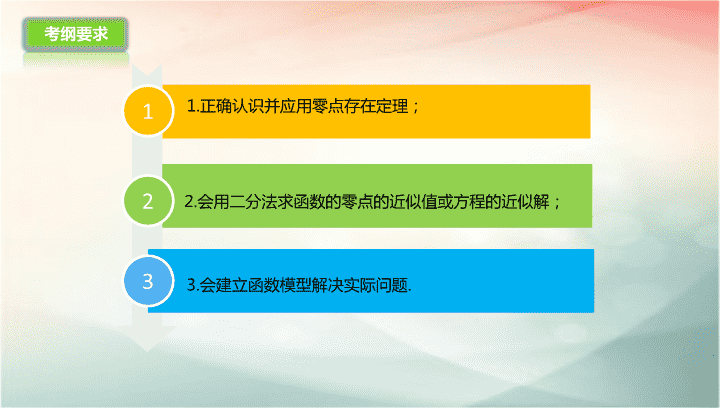
函数 的 应用 1 2 1. 正确认识并应用零点存在定理; 2. 会 用二分法求函数的零点的近似值或方程的近似解; 3 3. 会 建立函数模型解决实际问题 . 考纲要求 1 .对于函数 y = f(x) , x∈D ,使 f(x) = 0 的实数 x 叫做函数 y = f(x) , x∈D 的 . 2 .方程的根与函数的零点的关系:方程 f(x) = 0 有实数根 ⇔ _______________________ ⇔_____________________ . 3 .函数的零点存在定理:如果函数 y = f(x) 在区间 [a , b] 上的图象是一条连续不断的曲线,并且有 ________ ,那么,函数 y = f(x) 在区间 (a , b) 内有零点,即存在 c∈(a , b) ,使得 f(c) = 0. (1) 函数 y = f(x) 在区间 [a , b] 内若不连续,则 f(a)·f(b)<0 与函数 y = f(x) 在区间 (a , b) 内的零点个数没有关系 ( 即:零点存在定理仅对连续函数适用 ) . (2) 连续函数 y = f(x) 若满足 f(a)·f(b)<0 ,则在区间 (a , b) 内至少有一个零点;反过来,函数 y = f(x) 在区间 (a , b) 内有零点不一定使 f(a)·f(b)<0 成立,若 y = f(x) 为单调函数,则一定有 f(a)·f(b)<0. 知识梳理 零点 函数 y = f(x) 的图象与 x 轴有交点 函数y=f(x)有零点 f(a)·f(b)<0 4 .二分法只能求出连续函数变号零点,另外应注意初始区间的选择,依据给出的精确度,计算时及时检验. 5 .解决函数应用题关键在于理解题意,提高阅读能力.一方面要加强对常见函数模型的理解,弄清其产生的实际背景,把数学问题生活化;另一方面,要不断拓宽知识面.求解函数应用问题的思路和方法,我们可以用示意图表示为: 知识梳理 【例 1 】 (1)已知f(x)是定义在R上的奇函数,当x≥0时 , 则函数g(x)=f(x)-x+3的零点的集合为( ) A.{1,3} B.{-3,-1,1,3} C.{2- , 1,3} D.{-2- ,1,3} (2)函数 的零点个数是______. 【思路分析】 确定求函数零点个数的方法 典例精析 题型一: 函数的零点与方程的根 【规范解答】 (1)因为f(x)是定义在R上的奇函数,当x≥0时, 解 得x=1或x=3; 所以函数g(x)=f(x)-x+3的零点的集合为{-2- ,1,3}.故选D. 典例精析 (2)令 得x=± ,只有x= - 符合题意;令2x-6+ln x=0,得6-2x=ln x,在同一坐标系中作出函数y=6-2x和y=ln x的图象如图,观察知,图象有1个交点.所以函数f(x)有2个零点. 典例精析 确定函数零点的个数有两个基本方法: (1)利用图象研究与x轴的交点个数或转化成两个函数图象的交点个数定性判断. (2)利用零点存在性定理判断,但还需结合函数的图象和单调性,特别是二重根容易漏掉. 归纳总结 已知函数 在下列区间中,包含f(x)零点的区间是( ) A.(0,1) B.(1,2) C.(2,4) D.(4,+∞) 练一练 【解析】 因为函数f(x)在定义域(0,+∞)上是连续不断的,且f(2)=3-1>0, 所以,函数f(x)的零点在区间(2,4)内. C 【例 2 】若函数 f(x)= 有两个零点,则实数b的取值范围是__________. 典例精析 题型二: 函数零点的应用 【 思路分析 】 注意数形结合 【 规范解答 】 若函数 f(x) = 有两个零点,可得方程 有两个根,从而函数 y = | - 2| 与函数 y = b 的图象有两个交点,结合图象可得 0查看更多
相关文章
- 当前文档收益归属上传用户