【数学】2018届一轮复习人教A版2-4二次函数与幂函数学案

【数学】2018届一轮复习人教A版2-4二次函数与幂函数学案

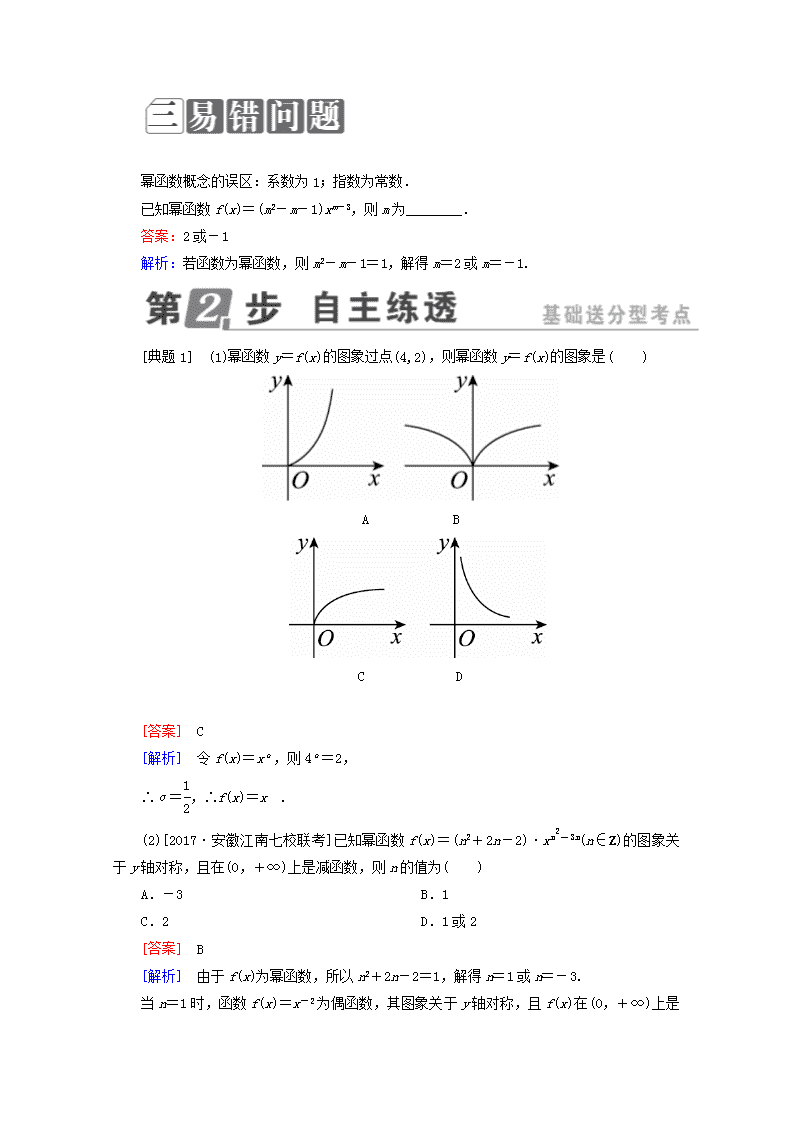
‎§2.4　二次函数与幂函数 考纲展示►　1.了解幂函数的概念．‎ ‎2．结合函数y＝x，y＝x2，y＝x3，y＝，y＝x的图象，了解它们的变化情况．‎ ‎3．理解并掌握二次函数的定义、图象及性质．‎ ‎4．能用二次函数、方程、不等式之间的关系解决简单问题．‎ 考点1　幂函数的图象与性质 五种常见幂函数的图象与性质 函数特征性质 y＝x y＝x2‎ y＝x3‎ y＝x y＝x－1‎ 图象 定义域 R R R ‎______‎ ‎______‎ 值域 R ‎______‎ R ‎______‎ ‎______‎ 奇偶性 ‎______‎ ‎______‎ ‎______‎ ‎______‎ ‎______‎ 单调性 ‎______‎ ‎______‎ ‎______‎ ‎______‎ ‎______‎ 公共点 ‎______‎ 答案：{x|x≥0}　{x|x≠0}　{y|y≥0}　{y|y≥0}　{y|y≠0}　奇　偶　奇　非奇非偶　奇 增　(－∞，0)减，(0，＋∞)增　增　增　(－∞，0)和(0，＋∞)减　(1,1)‎ ‎[教材习题改编]已知幂函数f(x)的图象过点(2，)，则函数f(x)＝________.‎ 答案：x 解析：设f(x)＝xα，则＝2α，所以α＝，故函数f(x)＝x.‎ 幂函数概念的误区：系数为1；指数为常数．‎ 已知幂函数f(x)＝(m2－m－1)xm－3，则m为________．‎ 答案：2或－1‎ 解析：若函数为幂函数，则m2－m－1＝1，解得m＝2或m＝－1.‎ ‎[典题1]　(1)幂函数y＝f(x)的图象过点(4,2)，则幂函数y＝f(x)的图象是(　　)‎ A　　 　　　B ‎　　‎ C　　 　　　D ‎[答案]　C ‎[解析]　令f(x)＝xα，则4α＝2，‎ ‎∴α＝，∴f(x)＝x.‎ ‎(2)[2017·安徽江南七校联考]已知幂函数f(x)＝(n2＋2n－2)·xn2－3n(n∈Z)的图象关于y轴对称，且在(0，＋∞)上是减函数，则n的值为(　　)‎ A．－3 B．1 ‎ C．2 D．1或2‎ ‎[答案]　B ‎[解析]　由于f(x)为幂函数，所以n2＋2n－2＝1，解得n＝1或n＝－3.‎ 当n＝1时，函数f(x)＝x－2为偶函数，其图象关于y轴对称，且f(x ‎)在(0，＋∞)上是减函数，所以n＝1满足题意；‎ 当n＝－3时，函数f(x)＝x18为偶函数，其图象关于y轴对称，而f(x)在(0，＋∞)上是增函数，所以n＝－3不满足题意，舍去．故选B.‎ ‎(3)1.1，0.9，1的大小关系为________．‎ ‎[答案]　0.9＜1＜1.1 ‎[解析]　把1看作1，幂函数y＝x在(0，＋∞)上是增函数．∵0＜0.9＜1＜1.1，∴0.9＜1＜1.1，即0.9＜1＜1.1.‎ ‎(4)已知函数f(x)＝若关于x的方程f(x)＝k有两个不同的实根，则实数k的取值范围是________．‎ ‎[答案]　(0,1)‎ ‎[解析]　作出函数y＝f(x)的图象如图．‎ 则当0＜k＜1时，关于x的方程f(x)＝k有两个不同的实根．‎ ‎[点石成金]　1.幂函数y＝xα的性质和图象由于α的取值不同而比较复杂，一般可从三方面考查：‎ ‎(1)α的正负：当α>0时，图象经过点(0,0)和点(1,1)，在第一象限的部分“上升”；当α<0时，图象不过点(0,0)，经过点(1,1)，在第一象限的部分“下降”；‎ ‎(2)曲线在第一象限的凹凸性：当α>1时曲线下凹；当0<α<1时曲线上凸，当α<0时曲线下凹；‎ ‎(3)函数的奇偶性：一般先将函数式化为正指数幂或根式形式，再根据函数定义域和奇偶性定义判断其奇偶性．‎ ‎2．在比较幂值的大小时，必须结合幂值的特点，选择适当的函数，借助其单调性进行比较．‎ 考点2　求二次函数的解析式 二次函数解析式的三种形式 ‎(1)一般式：f(x)＝____________；‎ ‎(2)顶点式：f(x)＝____________；‎ ‎(3)零点式：f(x)＝____________.‎ 答案：(1)ax2＋bx＋c(a≠0)　(2)a(x－m)2＋n(a≠0)　(3)a(x－x1)(x－x2)(a≠0)‎ 二次函数对称轴的判断方法：中值法；结论法．‎ ‎(1)对于二次函数y＝f(x)，如果定义域内有不同两点x1，x2且f(x1)＝f(x2)，那么函数y＝f(x)的图象关于直线________对称．‎ ‎(2)“二次函数y＝f(x)对定义域内所有x，都有f(a＋x)＝f(a－x)成立”的充要条件是“函数y＝f(x)的图象关于直线________对称”(a为常数)．‎ 答案：(1)x＝　(2)x＝a 解析：(1)作出二次函数y＝f(x)的图象(图略)，由图可知，当f(x1)＝f(x2)时，‎ 点P(x1，f(x1))，Q(x2，f(x2))关于直线x＝对称．‎ 由x1，x2的任意性，可得函数y＝f(x)的图象关于直线x＝对称．‎ ‎(2)由(1)可知，y＝f(x)的图象关于直线x＝a对称(a为常数).‎ ‎[典题2]　已知二次函数f(x)满足f(2)＝－1，f(－1)＝－1，且f(x)的最大值是8，试确定此二次函数的解析式．‎ ‎[解]　解法一(利用一般式)：‎ 设f(x)＝ax2＋bx＋c(a≠0)．‎ 由题意得解得 ‎∴所求二次函数的解析式为f(x)＝－4x2＋4x＋7.‎ 解法二(利用顶点式)：‎ 设f(x)＝a(x－m) 2＋n.‎ ‎∵f(2)＝f(－1)，‎ ‎∴抛物线的对称轴为x＝＝，‎ ‎∴m＝.‎ 又根据题意，函数有最大值8，∴n＝8，‎ ‎∴y＝f(x)＝a2＋8.‎ ‎∵f(2)＝－1，∴a2＋8＝－1，‎ 解得a＝－4，‎ ‎∴f(x)＝－42＋8＝－4x2＋4x＋7.‎ 解法三(利用零点式)：‎ 由已知f(x)＋1＝0两根为x1＝2，x2＝－1，‎ 故可设f(x)＋1＝a(x－2)(x＋1)，‎ 即f(x)＝ax2－ax－‎2a－1.‎ 又函数的最大值为ymax＝8，即＝8.解得a＝－4或a＝0(舍去)．‎ ‎∴所求函数的解析式为f(x)＝－4x2＋4x＋7.‎ ‎[点石成金]　求二次函数解析式的方法 根据已知条件确定二次函数的解析式，一般用待定系数法，选择规律如下：‎ ‎(1)已知三个点坐标，宜选用一般式；‎ ‎(2)已知顶点坐标、对称轴、最大(小)值等，宜选用顶点式；‎ ‎(3)已知图象与x轴两交点的坐标，宜选用零点式.‎ 为了美观，在加工太阳镜时将下半部分轮廓制作成二次函数图象的形状(如图所示)．若对应的两条曲线关于y轴对称，AE∥x轴，AB＝‎4 cm，最低点C在x轴上，高CH＝‎1 cm，BD＝‎2 cm，则右轮廓线DFE所在的二次函数的解析式为(　　)‎ ‎　‎ A．y＝(x＋3)2 B．y＝－(x－3) 2‎ C．y＝－(x＋3) 2 D．y＝(x－3) 2‎ 答案：D 解析：由题图可知，对应的两条曲线关于y轴对称，AE∥x轴，AB＝‎4 cm，最低点C在x轴上，高CH＝‎1 cm，BD＝‎2 cm，所以点C的纵坐标为0，横坐标的绝对值为＋＝3，即C(－3,0)．因为点F与点C关于y轴对称，所以F(3,0)，因为点F是右轮廓线DFE所在的二次函数图象的顶点，所以设该二次函数为y＝a(x－3) 2 (a>0)，将点D(1,1)代入得，a＝，即y＝(x－3) 2.‎ 考点3　二次函数的图象与性质 二次函数的图象和性质 f(x)＝ax2＋bx＋c a>0‎ a<0‎ 图象 定义域 R 值域 单调性 在上单调递减，在上单调递增 在上单调递增，在上单调递减 奇偶性 当b＝0时为偶函数；当b≠0时既不是奇函数也不是偶函数 图象特点 ‎①对称轴：x＝－；‎ ‎②顶点： ‎(1)[教材习题改编]若函数f(x)＝4x2－kx－8在[－1,2]上是单调函数，则实数k的取值范围是________．‎ 答案：(－∞，－8]∪[16，＋∞)‎ 解析：f(x)图象的对称轴方程是x＝，故≤－1或≥2，即k≤－8或k≥16.故所求k的取值范围是(－∞，－8]∪[16 ，＋∞)．‎ ‎(2)[教材习题改编]已知函数f(x)＝ax2＋x＋5的图象在x轴上方，则a的取值范围是________．‎ 答案： 解析：由题意，得 解得a>.‎ 二次函数单调性的求解误区：单调区间；在区间上单调．‎ 已知二次函数f(x)＝(k2－1)x2＋2x－3.‎ ‎(1)若函数f(x)的单调递增区间是(－∞，2]，则k＝________；‎ ‎(2)若函数f(x)在区间(－∞，2]上单调递增，则k满足________．‎ 答案：(1)±　(2)≤k<1或－10时，图象过原点和点(1,1)，在第一象限的图象上升；当α<0时，图象不过原点，在第一象限的图象下降，反之也成立．‎ ‎[易错防范]　1.对于函数y＝ax2＋bx＋c，要认为它是二次函数，就必须满足a≠0，当题目条件中未说明a≠0时，就要讨论a＝0和a≠0两种情况．‎ ‎2．幂函数的图象一定会出现在第一象限内，一定不会出现在第四象限，至于是否出现在第二、三象限内，要看函数的奇偶性；幂函数的图象最多只能同时出现在两个象限内；如果幂函数图象与坐标轴相交，则交点一定是原点．‎ ‎ 真题演练集训 ‎ ‎1．[2016·新课标全国卷Ⅲ]已知a＝2，b＝4，c＝25，则(　　)‎ A．b0)，g(x)＝logax的图象可能是(　　)‎ ‎　A　　　　　　　　B ‎　C　　　　　　　　D 答案：D 解析：当a>1时，函数f(x)＝xa(x>0)单调递增，函数g(x)＝logax单调递增，且过点(1,0)，由幂函数的图象性质可知C错；当00)单调遂增，函数g(x)＝logax单调递减，且过点(1,0)，排除A，又由幂函数的图象性质可知B错，故选D.‎ ‎4．[2013·重庆卷](－6≤a≤3)的最大值为(　　)‎ A. 9 B． C. 3 D． 答案：B 解析：易知函数y＝(3－a)(a＋6)的两个零点是3，－6，对称轴为a＝－，y＝(3－a)(a＋6)的最大值为y＝＝2，则的最大值为，故选B.‎ ‎5．[2014·辽宁卷]对于c＞0，当非零实数a，b满足‎4a2－2ab＋4b2－c＝0且使|‎2a＋b|最大时，－＋的最小值为________．‎ 答案：－2‎ 解析：设‎2a＋b＝x，则‎2a＝x－b，‎ ‎∴(x－b)2－b(x－b)＋4b2－c＝0，‎ x2－3bx＋6b2－c＝0，即6b2－3xb＋x2－c＝0.‎ ‎∴Δ＝9x2－4×6×(x2－c)≥0，‎ ‎∴3x2－8x2＋‎8c≥0，∴x2≤c.‎ 当|‎2a＋b|＝|x|取最大时，有(‎2a＋b)2＝c，‎ ‎∴‎4a2＋4ab＋b2＝c.‎ 又∵‎4a2－2ab＋4b2＝c，①‎ ‎∴＝，∴b＝a.‎ 将b＝a代入①，得 ‎4a‎2－‎2a·a＋a2·4＝c，‎ ‎∴a＝，b＝或a＝－，b＝－.‎ 当a＝，b＝时，有 －＋＝－＋ ‎＝－＋＝52－2≥－2，‎ 当＝，即c＝时等号成立．‎ 此时a＝，b＝.‎ 当a＝－，b＝－时，‎ －＋＝－＋＋＝＋＞0，‎ 综上可知，当c＝，a＝，b＝时，‎ min＝－2.‎ ‎ 课外拓展阅读 ‎ 构造二次函数解决问题 二次函数是中学数学的一个重要知识，它与一元二次不等式、一元二次方程的联系是诸多命题者的关注点．对于有些问题若能充分利用二次函数的性质，则会迎刃而解．下面就给出几种构造二次函数解决问题的例题．‎ ‎1．构造二次函数求根式函数的最值 ‎[典例1]　求函数y＝x2＋的最值．‎ ‎[思路分析]　利用换元法转化为二次函数求最值．‎ ‎[解]　令＝u，则x2＝1－u2，‎ 且0≤u≤1.‎ 所以y＝1－u2＋u＝－2＋，‎ 所以1≤y≤，故ymin＝1，ymax＝.‎ ‎2．构造二次函数解不等式 ‎(1)从结论的外形结构作形式联想进行构造 ‎[典例2]　已知ac时，f(x)<0.又a0，所以对于二次函数f(x)，‎ 当x＝时，f(x)有最小值，‎ 且f(x)min＝.‎ 所以f(x)≥，故原不等式成立．‎ ‎(3)利用根与系数的关系构造二次函数 ‎[典例4]　已知a>，b>，ab＝，求证：a＋b<1.‎ ‎[思路分析]　已知条件出现了ab＝，而结论中有a＋b，若设a＋b＝t，则a，b为二次函数f(x)＝x2－tx＋的图象与x轴的两个交点的横坐标，由于a>，b>，根据二次函数的性质，易证t<1.‎ ‎[证明]　设t＝a＋b，又ab＝，‎ 则a，b为二次函数f(x)＝x2－tx＋的图象与x轴的两个交点的横坐标．‎ 由于a>，b>，二次函数的图象开口向上，‎ 所以有f>0，即－t＋>0，‎ 解得t<1，即a＋b<1.‎