2011年高考数学真题分类汇编N
课标理数5.N1[2011·北京卷] 如图1-2,AD,AE,BC分别与圆O切于点D,E,F,延长AF与圆O交于另一点G.
图1-2
给出下列三个结论:
①AD+AE=AB+BC+CA;
②AF·AG=AD·AE;
③△AFB∽△ADG.
其中正确结论的序号是( )
A.①② B.②③
C.①③ D.①②③
课标理数5.N1[2011·北京卷] A 【解析】 因为AD、AE、BC分别与圆O切于点D、E、F,所以AD=AE,BD=BF,CF=CE,又AD=AB+BD,所以AD=AB+BF,同理有AE=CA+FC.又BC=BF+FC,所以AD+AE=AB+BC+CA,故①正确;对②,由切割线定理有:AD2=AF·AG,又AD=AE,所以有AF·AG=AD·AE成立;对③,很显然,∠ABF≠∠AGD,所以③不正确,故应选A.
图1-2
课标理数15.N1[2011·广东卷] (几何证明选讲选做题)如图1-2,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,C是圆上一点使得BC=5,∠BAC=∠APB,则AB=________.
课标理数15.N1[2011·广东卷] 【解析】 因为PA为圆O切线,所以∠PAB=∠ACB,又∠APB=∠BAC,
所以△PAB∽△ACB,所以=,所以AB2=PB·CB=35,所以AB=.
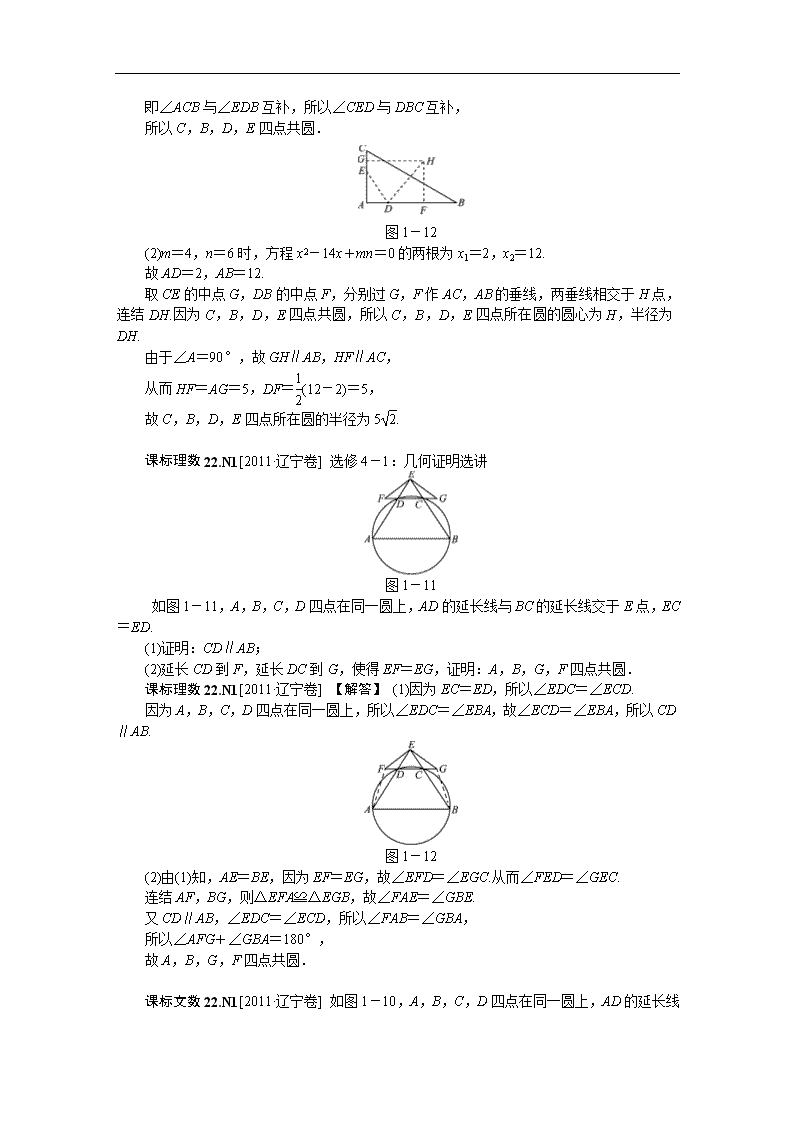
课标文数15.N1[2011·广东卷] (几何证明选讲选做题)如图1-3,在梯形ABCD中,AB∥CD,AB=4,CD=2,
图1-3
E、F分别为AD、BC上点,且EF=3,EF∥AB,则梯形ABFE与梯形EFCD的面积比
为________.
课标文数15.N1[2011·广东卷] 7∶5
图1-4
【解析】 图1-4延长AD与BC交于H点,由于DC∥EF∥AB,又=,
所以=,同理=,所以S△HDC∶S梯形DEFC∶S梯形EFBA=4∶5∶7,
所以梯形ABFE与梯形EFCD的面积比为7∶5.
图1-2
课标理数11.N1[2011·湖南卷] 如图1-2,A,E是半圆周上的两个三等分点,直径BC=4,AD⊥BC,垂足为D,BE与AD相交于点F,则AF的长为________.
课标理数11.N1[2011·湖南卷] 【解析】 连结AO与AB,因为A,E是半圆上的三等分点,所以∠ABO=60°,∠EBO=30°.
因为OA=OB=2,所以△ABO为等边三角形.又因为∠EBO=30°,∠BAD=30°,所以F为△ABO的中心,易得AF=.
课标理数22.N1[2011·课标全国卷]
图1-11
如图1-11,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合,已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
课标理数22.N1[2011·课标全国卷] 【解答】 (1)证明:连结DE,根据题意在△ADE和△ACB中,AD×AB=mn=AE×AC,
即=,又∠DAE=∠CAB,从而△ADE∽△ACB,
因此∠ADE=∠ACB,
即∠ACB与∠EDB互补,所以∠CED与DBC互补,
所以C,B,D,E四点共圆.
图1-12
(2)m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.
故AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连结DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=90°,故GH∥AB,HF∥AC,
从而HF=AG=5,DF=(12-2)=5,
故C,B,D,E四点所在圆的半径为5.
课标理数22.N1[2011·辽宁卷] 选修4-1:几何证明选讲
图1-11
如图1-11,A,B,C,D四点在同一圆上,AD的延长线与BC的延长线交于E点,EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
课标理数22.N1[2011·辽宁卷] 【解答】 (1)因为EC=ED,所以∠EDC=∠ECD.
因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA,故∠ECD=∠EBA,所以CD∥AB.
图1-12
(2)由(1)知,AE=BE,因为EF=EG,故∠EFD=∠EGC.从而∠FED=∠GEC.
连结AF,BG,则△EFA≌△EGB,故∠FAE=∠GBE.
又CD∥AB,∠EDC=∠ECD,所以∠FAB=∠GBA,
所以∠AFG+∠GBA=180°,
故A,B,G,F四点共圆.
课标文数22.N1[2011·辽宁卷] 如图1-10,A,B,C,D四点在同一圆上,AD的延长线
图1-10
与BC的延长线交于E点,且EC=ED.
(1)证明:CD∥AB;
(2)延长CD到F,延长DC到G,使得EF=EG,证明:A,B,G,F四点共圆.
课标文数22.N1[2011·辽宁卷] 【解答】 (1)因为EC=ED,所以∠EDC=∠ECD.
图1-11
因为A,B,C,D四点在同一圆上,所以∠EDC=∠EBA.
故∠ECD=∠EBA.
所以CD∥AB.
(2)由(1)知,AE=BE,因为EF=EG,故∠EFD=∠EGC,
从而∠FED=∠GEC.
连接AF,BG,则△EFA≌△EGB,故∠FAE=∠GBE.
又CD∥AB,∠EDC=∠ECD,所以∠FAB=∠GBA.
所以∠AFG+∠GBA=180°.
故A,B,G,F四点共圆.
课标文数22.N1[2011·课标全国卷] 如图1-10,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.
图1-10
已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.
(1)证明:C,B,D,E四点共圆;
(2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.
课标文数22.N1[2011·课标全国卷]
图1-11
【解答】 (1)证明:连结DE,根据题意在△ADE和△ACB中,AD×AB=mn=AE×AC,
即=,又∠DAE=∠CAB ,从而△ADE∽△ACB.
因此∠ADE=∠ACB,
即∠ACB与∠EDB互补,所以∠CED与∠DBC互补,
所以C,B,D,E四点共圆.
(2)m=4,n=6时,方程x2-14x+mn=0的两根为x1=2,x2=12.
故AD=2,AB=12.
取CE的中点G,DB的中点F,分别过G,F作AC,AB的垂线,两垂线相交于H点,连结DH.因为C,B,D,E四点共圆,所以C,B,D,E四点所在圆的圆心为H,半径为DH.
由于∠A=90°,故GH∥AB,HF∥AC,从而HF=AG=5,DF=(12-2)=5.
故C,B,D,E四点所在圆的半径为5.
课标理数15.[2011·陕西卷] (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
N4A.(不等式选做题)若关于x的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a的取值范围是____________.
图1-5
N1B.(几何证明选做题)如图1-5,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=________.
N3C.(坐标系与参数方程选做题)直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
课标理数15.(1)N4[2011·陕西卷] a≥3或a≤-3
【解析】 令t=|x+1|+|x-2|得t的最小值为3,即有|a|≥3,解得a≥3或a≤-3.
课标理数15.(2)N1[2011·陕西卷] 4 【解析】 在Rt△ADC中,CD=8;在Rt△ADC与Rt△ABE中,∠B=∠D,所以△ADC∽△ABE,故=,BE=×CD=4.
课标理数15.(3)N3[2011·陕西卷] 3 【解析】 由C1:消参得(x-3)2+(y-4)2=1;由C2:ρ=1得x2+y2=1,两圆圆心距为5,两圆半径都为1,故|AB|≥3,最小值为3.
课标文数15.[2011·陕西卷] N4A.(不等式选做题)若不等式|x+1|+|x-2|≥a对任意x∈R恒成立,则a的取值范围是________.
图1-7
N1B.(几何证明选做题)如图1-7,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则AE=________.
N3C.(坐标系与参数方程选做题)直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
课标文数15A.N4[2011·陕西卷] (-∞,3] 【解析】 由绝对值的几何意义得|x+1|+|x-2|≥3,要使得|x+1|+|x-2|≥a恒成立,则a≤3,即a∈(-∞,3].
课标文数15B.N1[2011·陕西卷] 2 【解析】 根据图形由∠ACD=90°,∠B=∠D,得A,B,C,D四点共圆,连接BD,则∠DBA=90°,AB=6,AD=12,所以∠BDA=30°=∠BCA.因为AE⊥BC,AE=AC=2.
课标文数15C.N3[2011·陕西卷] 1 【解析】 由C1:消参得(x-3)2+y2=1,由C2:ρ=1得x2+y2=1,两圆圆心距为3,两圆半径都为1,故|AB|≥1,最小值为1.
课标数学21.[2011·江苏卷]
【选做题】 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.
解答时应写出文字说明、证明过程或演算步骤.
图1-7
N1 A.选修4-1:几何证明选讲
如图1-7,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB∶AC为定值.
N2 B.选修4-2:矩阵与变换
已知矩阵A=,向量β=.求向量α,使得A2α=β.
N3 C.选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,求过椭圆(φ为参数)的右焦点,且与直线(t为参数)平行的直线的普通方程.
N4 D.选修4-5:不等式选讲
解不等式x+|2x-1|<3.
课标数学21.[2011·江苏卷] N1 A.选修4-1:几何证明选讲 本题主要考查两圆内切、相似比等基础知识,考查推理论证能力.
【解答】 证明:连结AO1,并延长分别交两圆于点E和点D.连结BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上,故AD,AE分别为圆O1,圆O2的直径.
从而∠ABD=∠ACE=,所以BD∥CE,
于是===.
所以AB∶AC为定值.
N2 B.选修4-2:矩阵与变换 本题主要考查矩阵运算等基础知识,考查运算求 解能力.
【解答】 A2==.
设α=.由A2α=β,得=,从而
解得x=-1,y=2,所以α=.
N3 C.选修4-4:坐标系与参数方程 本题主要考查椭圆及直线的参数方程等基础知识,考查转化问题的能力.
【解答】 由题设知,椭圆的长半轴长a=5,短半轴长b=3,从而c==4,所以右焦点为(4,0).将已知直线的参数方程化为普通方程:x-2y+2=0.
故所求直线的斜率为,因此其方程为y=(x-4),即x-2y-4=0.
N4 D.选修4-5:不等式选讲 本题主要考查解绝对值不等式的基础知识,考查分类讨论、运算求解能力.
【解答】 原不等式可化为
或
解得≤x<或-2
0),则BF=2k,BE=k.
由DF·FC=AF·BF,得2=8k2,即k=.
∴AF=2,BF=1,BE=,AE=,
由切割线定理得CE2=BE·EA=×=,
∴CE=.
课标文数13.N1[2011·天津卷] 如图1-5,已知圆中两条弦AB与CD相交于点F,E是AB延长线上一点,且DF=CF=,AF∶FB∶BE=4∶2∶1.若CE与圆相切,则线段CE的长为________.
图1-5
课标文数13.N1[2011·天津卷] 【解析】 设AF=4k(k>0),则BF=2k,BE=k.
由DF·FC=AF·BF得2=8k2,即k=.
∴AF=2,BF=1,BE=,AE=,
由切割线定理得CE2=BE·EA=×=,
∴CE=.
课标理数21.[2011·福建卷]
N2(1)选修4-2:矩阵与变换
设矩阵M=(其中a>0,b>0).
①若a=2,b=3,求矩阵M的逆矩阵M-1;
②若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′:+y2=1,求a,b的值.
N3(2)坐标系选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为(α为参数).
①已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为,判断点P与直线l的位置关系;
②设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
N4(3)选修4-5:不等式选讲
设不等式|2x-1|<1的解集为M.
①求集合M;
②若a,b∈M,试比较ab+1与a+b的大小.
课标理数21.[2011·福建卷] 【解答】 N2(1)①设矩阵M的逆矩阵M-1=),则MM-1=).
又M=),所以))=).
所以2x1=1,2y1=0,3x2=0,3y2=1,即x1=,y1=0,x2=0,y2=.
故所求的逆矩阵M-1=).
②设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P′(x′,y′).
则))=),即
又点P′(x′,y′)在曲线C′上,所以+y′2=1.
则+b2y2=1为曲线C的方程.
又已知曲线C的方程为x2+y2=1,故
又a>0,b>0,所以
N3(2)①把极坐标系下的点P化为直角坐标,
得P(0,4).
因为点P的直角坐标(0,4)满足直线l的方程x-y+4=0,所以点P在直线l上.
②因为点Q在曲线C上,故可设点Q的坐标为(cosα,sinα),
从而点Q到直线l的距离为
d==
=cos+2.
由此得,当cos=-1时,d取得最小值,且最小值为.
N4(3)①由|2x-1|<1得-1<2x-1<1,解得00.
故ab+1>a+b.
课标数学21.[2011·江苏卷]
【选做题】 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.
解答时应写出文字说明、证明过程或演算步骤.
图1-7
N1 A.选修4-1:几何证明选讲
如图1-7,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB∶AC为定值.
N2 B.选修4-2:矩阵与变换
已知矩阵A=,向量β=.求向量α,使得A2α=β.
N3 C.选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,求过椭圆(φ为参数)的右焦点,且与直线(t为参数)平行的直线的普通方程.
N4 D.选修4-5:不等式选讲
解不等式x+|2x-1|<3.
课标数学21.[2011·江苏卷] N1 A.选修4-1:几何证明选讲 本题主要考查两圆内切、相似比等基础知识,考查推理论证能力.
【解答】 证明:连结AO1,并延长分别交两圆于点E和点D.连结BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上,故AD,AE分别为圆O1,圆O2的直径.
从而∠ABD=∠ACE=,所以BD∥CE,
于是===.
所以AB∶AC为定值.
N2 B.选修4-2:矩阵与变换 本题主要考查矩阵运算等基础知识,考查运算求 解能力.
【解答】 A2==.
设α=.由A2α=β,得=,从而
解得x=-1,y=2,所以α=.
N3 C.选修4-4:坐标系与参数方程 本题主要考查椭圆及直线的参数方程等基础知识,考查转化问题的能力.
【解答】 由题设知,椭圆的长半轴长a=5,短半轴长b=3,从而c==4,所以右焦点为(4,0).将已知直线的参数方程化为普通方程:x-2y+2=0.
故所求直线的斜率为,因此其方程为y=(x-4),即x-2y-4=0.
N4 D.选修4-5:不等式选讲 本题主要考查解绝对值不等式的基础知识,考查分类讨论、运算求解能力.
【解答】 原不等式可化为
或
解得≤x<或-20,b>0).
①若a=2,b=3,求矩阵M的逆矩阵M-1;
②若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′:+y2=1,求a,b的值.
N3(2)坐标系选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为(α为参数).
①已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为,判断点P与直线l的位置关系;
②设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
N4(3)选修4-5:不等式选讲
设不等式|2x-1|<1的解集为M.
①求集合M;
②若a,b∈M,试比较ab+1与a+b的大小.
课标理数21.[2011·福建卷] 【解答】 N2(1)①设矩阵M的逆矩阵M-1=),则MM-1=).
又M=),所以))=).
所以2x1=1,2y1=0,3x2=0,3y2=1,即x1=,y1=0,x2=0,y2=.
故所求的逆矩阵M-1=).
②设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P′(x′,y′).
则))=),即
又点P′(x′,y′)在曲线C′上,所以+y′2=1.
则+b2y2=1为曲线C的方程.
又已知曲线C的方程为x2+y2=1,故
又a>0,b>0,所以
N3(2)①把极坐标系下的点P化为直角坐标,
得P(0,4).
因为点P的直角坐标(0,4)满足直线l的方程x-y+4=0,所以点P在直线l上.
②因为点Q在曲线C上,故可设点Q的坐标为(cosα,sinα),
从而点Q到直线l的距离为
d==
=cos+2.
由此得,当cos=-1时,d取得最小值,且最小值为.
N4(3)①由|2x-1|<1得-1<2x-1<1,解得00.
故ab+1>a+b.
课标理数14.N3[2011·广东卷] (坐标系与参数方程选做题)已知两曲线参数方程分别为
(0≤θ<π)和(t∈R),它们的交点坐标为________.
课标理数14.N3[2011·广东卷] 【解析】 把参数方程化为标准方程得+y2=1(y≥0),把化为标准方程得y2=x(x>0),联立方程得x=1或x=-5(舍去),
把x=1代入y2=x得y=或y=-(舍去),所以交点坐标为.
课标理数9.N3[2011·湖南卷] 在直角坐标系xOy中,曲线C1的参数方程为(α为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为ρ(cosθ-sinθ)+1=0,则C1与C2的交点个数为________.
课标理数9. N3[2011·湖南卷] 2 【解析】 曲线C1的参数方程化为普通方程:x2+(y-1)2=1,圆心为(0,1),r=1,曲线C2的方程为ρ(cosθ-sinθ)+1=0化为普通方程:x-y+1=0,
则圆心在曲线C2上,直线与圆相交,故C1与C2的交点个数为2.
课标文数9.N3[2011·湖南卷] 在直角坐标系xOy中,曲线C1的参数方程为(α为参数).在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,曲线C2的方程为ρ(cosθ-sinθ)+1=0,则C1与C2的交点个数为________.
课标文数9.N3[2011·湖南卷] 2 【解析】 曲线C1的参数方程为化为普通方程:+=1 ①,
曲线C2的方程为ρ(cosθ-sinθ)+1=0化为普通方程:x-y+1=0 ②.
联立①,②得7x2+8x-8=0,此时Δ=82-4×7×(-8)>0.故C1与C2的交点个数为2.
课标理数15.N3[2011·江西卷] (1)(坐标系与参数方程选做题)若曲线的极坐标方程为ρ=2sinθ+4cosθ,以极点为原点,极轴为x轴正半轴建立直角坐标系,则该曲线的直角坐标方程为________.
课标理数15.N3[2011·江西卷] 【答案】 x2+y2-4x-2y=0
【解析】 (1)由 ⇒cosθ=,sinθ=,ρ2=x2+y2,代入ρ=2sinθ+4cosθ得,ρ=+⇒ρ2=2y+4x⇒x2+y2-4x-2y=0.
课标理数23.N3[2011·课标全国卷] 在直角坐标系xOy中,曲线C1的参数方程为(α为参数)
M是C1上的动点,P点满足=2,P点的轨迹为曲线C2.
(1)求C2的参数方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,
射线θ=与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
课标理数23.N3[2011·课标全国卷] 【解答】 (1)设P(x,y),则由条件知M,由于M点在C1上,所以
即
从而C2的参数方程为
(α为参数)
(2)曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ.
射线θ=与C1的交点A的极径为ρ1=4sin,
射线θ=与C2的交点B的极径为ρ2=8sin.
所以|AB|=|ρ1-ρ2|=2.
课标理数23.N3[2011·辽宁卷] 选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为(φ为参数),曲线C2的参数方程为(a>b>0,φ为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当α=时,l与C1,C2的交点分别为A1,B1,当α=-时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
课标理数23.N3[2011·辽宁卷] 【解答】 (1)C1是圆,C2是椭圆.
当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0).
因为这两点间的距离为2,所以a=3.
当α=时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b).
因为这两点重合,所以b=1.
(2)C1,C2的普通方程分别为x2+y2=1和+y2=1.
当α=时,射线l与C1交点A1的横坐标为x=,与C2交点B1的横坐标为x′=.
当α=-时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称.因此四边形A1A2B2B1为梯形,故四边形A1A2B2B1的面积为=.
课标文数23.N3[2011·辽宁卷] 在平面直角坐标系xOy中,曲线C1的参数方程为(φ为参数),曲线C2的参数方程为(a>b>0,φ为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α与C1,C2各有一个交点.当α=0时,这两个交点间的距离为2,当α=时,这两个交点重合.
(1)分别说明C1,C2是什么曲线,并求出a与b的值;
(2)设当α=时,l与C1,C2的交点分别为A1,B1,当α=-时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
课标文数23.N3[2011·辽宁卷] 【解答】 (1)C1是圆,C2是椭圆.
当α=0时,射线l与C1,C2交点的直角坐标分别为(1,0),(a,0),因为这两点间的距离为2,所以a=3.
当α=时,射线l与C1,C2交点的直角坐标分别为(0,1),(0,b),因为这两点重合,所以b=1.
(2)C1,C2的普通方程分别为x2+y2=1和+y2=1.
当α=时,射线l与C1交点A1的横坐标为x=,与C2交点B1的横坐标为x′=.
当α=-时,射线l与C1,C2的两个交点A2,B2分别与A1,B1关于x轴对称,因此四边形A1A2B2B1为梯形.
故四边形A1A2B2B1的面积为=.
课标文数23.N3[2011·课标全国卷] 在直角坐标系xOy中,曲线C1的参数方程为(α为参数)
M是C1上的动点,P点满足=2,P点的轨迹为曲线C2.
(1)求C2的参数方程;
(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ=与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.
课标文数23.N3[2011·课标全国卷] 【解答】 (1)设P(x,y),则由条件知M,由于M点在C1上,所以
即
从而C2的参数方程为(α为参数)
(2)曲线C1的极坐标方程为ρ=4sinθ,曲线C2的极坐标方程为ρ=8sinθ.
射线θ=与C1的交点A的极径为ρ1=4sin,
射线θ=与C2的交点B的极径为ρ2=8sin.
所以|AB|=|ρ2-ρ1|=2.
课标理数15.[2011·陕西卷] (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
N4A.(不等式选做题)若关于x的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a的取值范围是____________.
图1-5
N1B.(几何证明选做题)如图1-5,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=________.
N3C.(坐标系与参数方程选做题)直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
课标理数15.(1)N4[2011·陕西卷] a≥3或a≤-3
【解析】 令t=|x+1|+|x-2|得t的最小值为3,即有|a|≥3,解得a≥3或a≤-3.
课标理数15.(2)N1[2011·陕西卷] 4 【解析】 在Rt△ADC中,CD=8;在Rt△ADC与Rt△ABE中,∠B=∠D,所以△ADC∽△ABE,故=,BE=×CD=4.
课标理数15.(3)N3[2011·陕西卷] 3 【解析】 由C1:消参得(x-3)2+(y-4)2=1;由C2:ρ=1得x2+y2=1,两圆圆心距为5,两圆半径都为1,故|AB|≥3,最小值为3.
课标文数15.[2011·陕西卷] N4A.(不等式选做题)若不等式|x+1|+|x-2|≥a对任意x∈R恒成立,则a的取值范围是________.
图1-7
N1B.(几何证明选做题)如图1-7,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则AE=________.
N3C.(坐标系与参数方程选做题)直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
课标文数15A.N4[2011·陕西卷] (-∞,3] 【解析】 由绝对值的几何意义得|x+1|+|x-2|≥3,要使得|x+1|+|x-2|≥a恒成立,则a≤3,即a∈(-∞,3].
课标文数15B.N1[2011·陕西卷] 2 【解析】 根据图形由∠ACD=90°,∠B=∠D,得A,B,C,D四点共圆,连接BD,则∠DBA=90°,AB=6,AD=12,所以∠BDA=30°=∠BCA.因为AE⊥BC,AE=AC=2.
课标文数15C.N3[2011·陕西卷] 1 【解析】 由C1:消参得(x-3)2+y2=1,由C2:ρ=1得x2+y2=1,两圆圆心距为3,两圆半径都为1,故|AB|≥1,最小值为1.
课标数学21.[2011·江苏卷]
【选做题】 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.
解答时应写出文字说明、证明过程或演算步骤.
图1-7
N1 A.选修4-1:几何证明选讲
如图1-7,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆O2于点C(O1不在AB上).求证:AB∶AC为定值.
N2 B.选修4-2:矩阵与变换
已知矩阵A=,向量β=.求向量α,使得A2α=β.
N3 C.选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,求过椭圆(φ为参数)的右焦点,且与直线(t为参数)平行的直线的普通方程.
N4 D.选修4-5:不等式选讲
解不等式x+|2x-1|<3.
课标数学21.[2011·江苏卷] N1 A.选修4-1:几何证明选讲 本题主要考查两圆内切、相似比等基础知识,考查推理论证能力.
【解答】 证明:连结AO1,并延长分别交两圆于点E和点D.连结BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上,故AD,AE分别为圆O1,圆O2的直径.
从而∠ABD=∠ACE=,所以BD∥CE,
于是===.
所以AB∶AC为定值.
N2 B.选修4-2:矩阵与变换 本题主要考查矩阵运算等基础知识,考查运算求 解能力.
【解答】 A2==.
设α=.由A2α=β,得=,从而
解得x=-1,y=2,所以α=.
N3 C.选修4-4:坐标系与参数方程 本题主要考查椭圆及直线的参数方程等基础知识,考查转化问题的能力.
【解答】 由题设知,椭圆的长半轴长a=5,短半轴长b=3,从而c==4,所以右焦点为(4,0).将已知直线的参数方程化为普通方程:x-2y+2=0.
故所求直线的斜率为,因此其方程为y=(x-4),即x-2y-4=0.
N4 D.选修4-5:不等式选讲 本题主要考查解绝对值不等式的基础知识,考查分类讨论、运算求解能力.
【解答】 原不等式可化为
或
解得≤x<或-20)相切,则r=________.
课标理数11.N3[2011·天津卷] 【解析】 由抛物线的参数方程 消去t,得y2=8x,∴焦点坐标为(2,0).
∴直线l的方程为y=x-2.
又∵直线l与圆(x-4)2+y2=r2相切,
∴r==.
课标理数21.[2011·福建卷]
N2(1)选修4-2:矩阵与变换
设矩阵M=)(其中a>0,b>0).
①若a=2,b=3,求矩阵M的逆矩阵M-1;
②若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C′:+y2=1,求a,b的值.
N3(2)坐标系选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线l的方程为x-y+4=0,曲线C的参数方程为(α为参数).
①已知在极坐标系(与直角坐标系xOy取相同的长度单位,且以原点O为极点,以x轴正半轴为极轴)中,点P的极坐标为,判断点P与直线l的位置关系;
②设点Q是曲线C上的一个动点,求它到直线l的距离的最小值.
N4(3)选修4-5:不等式选讲
设不等式|2x-1|<1的解集为M.
①求集合M;
②若a,b∈M,试比较ab+1与a+b的大小.
课标理数21.[2011·福建卷] 【解答】 N2(1)①设矩阵M的逆矩阵M-1=),则MM-1=).
又M=),所以))=).
所以2x1=1,2y1=0,3x2=0,3y2=1,即x1=,y1=0,x2=0,y2=.
故所求的逆矩阵M-1=).
②设曲线C上任意一点P(x,y),它在矩阵M所对应的线性变换作用下得到点P′(x′,y′).
则))=),即
又点P′(x′,y′)在曲线C′上,所以+y′2=1.
则+b2y2=1为曲线C的方程.
又已知曲线C的方程为x2+y2=1,故
又a>0,b>0,所以
N3(2)①把极坐标系下的点P化为直角坐标,
得P(0,4).
因为点P的直角坐标(0,4)满足直线l的方程x-y+4=0,所以点P在直线l上.
②因为点Q在曲线C上,故可设点Q的坐标为(cosα,sinα),
从而点Q到直线l的距离为
d==
=cos+2.
由此得,当cos=-1时,d取得最小值,且最小值为.
N4(3)①由|2x-1|<1得-1<2x-1<1,解得00.
故ab+1>a+b.
课标理数10.N4,E6[2011·湖南卷] 设x,y∈R,且xy≠0,则的最小值为________.
课标理数10.N4,E6[2011·湖南卷] 9 【解析】 方法一:=1+4x2y2++4≥5+2=9,当且仅当4x2y2=时,“=”成立.
方法二:利用柯西不等式:≥=9,当且仅当4x2y2=时,等号成立.
课标理数15.N4[2011·江西卷] (2)(不等式选做题)对于实数x,y,若|x-1|≤1,|y-2|≤1,则|x-2y+1|的最大值为________.
课标理数15.N4[2011·江西卷] 【答案】 5
【解析】 |x-2y+1|=|(x-1)-2(y-1)|≤|x-1|+|2(y-2)+2|≤1+2|y-2|+2≤5,当x=0,y=3时,|x-2y+1|取得最大值5.
课标文数15.N4[2011·江西卷] 对于x∈R,不等式-≥8的解集为________.
课标文数15.N4[2011·江西卷] [0,+∞) 【解析】 由题意可得
或或解得x∈[0,+∞).
课标理数24.N4[2011·课标全国卷] 设函数f(x)=|x-a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)≥3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
课标理数24.N4[2011·课标全国卷] 【解答】 (1)当a=1时,f(x)≥3x+2可化为|x-1|≥2.
由此可得x≥3或x≤-1.
故不等式f(x)≥3x+2的解集为
{x|x≥3或x≤-1}.
(2)由f(x)≤0得
|x-a|+3x≤0.
此不等式可化为不等式组
或
即或
因为a>0,所以不等式组的解集为.
由题设可得-=-1,故a=2.
课标理数24.N4[2011·辽宁卷] 选修4-5:不等式选讲
已知函数f(x)=|x-2|-|x-5|.
(1)证明:-3≤f(x)≤3;
(2)求不等式f(x)≥x2-8x+15的解集.
课标理数24.N4[2011·辽宁卷] 【解答】 (1)f(x)=|x-2|-|x-5|=
当2<x<5时,-3<2x-7<3.
所以-3≤f(x)≤3.
(2)由(1)可知,
当x≤2时,f(x)≥x2-8x+15的解集为空集;
当2<x<5时,f(x)≥x2-8x+15的解集为{x|5-≤x<5};
当x≥5时,f(x)≥x2-8x+15的解集为{x|5≤x≤6}.
综上,不等式f(x)≥x2-8x+15的解集为{x|5-≤x≤6}.
课标文数24.N4[2011·辽宁卷] 已知函数f(x)=|x-2|-|x-5|.
(1)证明:-3≤f(x)≤3;
(2)求不等式f(x)≥x2-8x+15的解集.
课标文数24.N4[2011·辽宁卷] 【解答】
(1)f(x)=|x-2|-|x-5|=
当2<x<5时,-3<2x-7<3.
所以-3≤f(x)≤3.
(2)由(1)可知,
当x≤2时,f(x)≥x2-8x+15的解集为空集;
当2<x<5时,f(x)≥x2-8x+15的解集为{x|5-≤x<5};
当x≥5时,f(x)≥x2-8x+15的解集为{x|5≤x≤6}.
综上,不等式f(x)≥x2-8x+15的解集为{x|5-≤x≤6}.
课标文数24.N4[2011·课标全国卷] 设函数f(x)=|x-a|+3x,其中a>0.
(1)当a=1时,求不等式f(x)≥3x+2的解集;
(2)若不等式f(x)≤0的解集为{x|x≤-1},求a的值.
课标文数24.N4[2011·课标全国卷] 【解答】 (1)当a=1时,f(x)≥3x+2可化为|x-1|≥2.
由此可得x≥3或x≤-1,
故不等式f(x)≥3x+2的解集为
{x|x≥3或x≤-1}.
(2)由f(x)≤0得|x-a|+3x≤0.
此不等式可化为不等式组
或
即或
因为a>0,所以不等式组的解集为.
由题设可得-=-1,故a=2.
课标理数15.[2011·陕西卷] (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
N4A.(不等式选做题)若关于x的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a的取值范围是____________.
图1-5
N1B.(几何证明选做题)如图1-5,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则BE=________.
N3C.(坐标系与参数方程选做题)直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
课标理数15.(1)N4[2011·陕西卷] a≥3或a≤-3
【解析】 令t=|x+1|+|x-2|得t的最小值为3,即有|a|≥3,解得a≥3或a≤-3.
课标理数15.(2)N1[2011·陕西卷] 4 【解析】 在Rt△ADC中,CD=8;在Rt△ADC与
Rt△ABE中,∠B=∠D,所以△ADC∽△ABE,故=,BE=×CD=4.
课标理数15.(3)N3[2011·陕西卷] 3 【解析】 由C1:消参得(x-3)2+(y-4)2=1;由C2:ρ=1得x2+y2=1,两圆圆心距为5,两圆半径都为1,故|AB|≥3,最小值为3.
课标文数15.[2011·陕西卷] N4A.(不等式选做题)若不等式|x+1|+|x-2|≥a对任意x∈R恒成立,则a的取值范围是________.
图1-7
N1B.(几何证明选做题)如图1-7,∠B=∠D,AE⊥BC,∠ACD=90°,且AB=6,AC=4,AD=12,则AE=________.
N3C.(坐标系与参数方程选做题)直角坐标系xOy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为________.
课标文数15A.N4[2011·陕西卷] (-∞,3] 【解析】 由绝对值的几何意义得|x+1|+|x-2|≥3,要使得|x+1|+|x-2|≥a恒成立,则a≤3,即a∈(-∞,3].
课标文数15B.N1[2011·陕西卷] 2 【解析】 根据图形由∠ACD=90°,∠B=∠D,得A,B,C,D四点共圆,连接BD,则∠DBA=90°,AB=6,AD=12,所以∠BDA=30°=∠BCA.因为AE⊥BC,AE=AC=2.
课标文数15C.N3[2011·陕西卷] 1 【解析】 由C1:消参得(x-3)2+y2=1,由C2:ρ=1得x2+y2=1,两圆圆心距为3,两圆半径都为1,故|AB|≥1,最小值为1.
课标数学21.[2011·江苏卷]
【选做题】 本题包括A、B、C、D四小题,请选定其中两题,并在相应的答题区域内作答.若多做,则按作答的前两题评分.
解答时应写出文字说明、证明过程或演算步骤.
图1-7
N1 A.选修4-1:几何证明选讲
如图1-7,圆O1与圆O2内切于点A,其半径分别为r1与r2(r1>r2).圆O1的弦AB交圆
O2于点C(O1不在AB上).求证:AB∶AC为定值.
N2 B.选修4-2:矩阵与变换
已知矩阵A=,向量β=.求向量α,使得A2α=β.
N3 C.选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,求过椭圆(φ为参数)的右焦点,且与直线(t为参数)平行的直线的普通方程.
N4 D.选修4-5:不等式选讲
解不等式x+|2x-1|<3.
课标数学21.[2011·江苏卷] N1 A.选修4-1:几何证明选讲 本题主要考查两圆内切、相似比等基础知识,考查推理论证能力.
【解答】 证明:连结AO1,并延长分别交两圆于点E和点D.连结BD,CE.
因为圆O1与圆O2内切于点A,所以点O2在AD上,故AD,AE分别为圆O1,圆O2的直径.
从而∠ABD=∠ACE=,所以BD∥CE,
于是===.
所以AB∶AC为定值.
N2 B.选修4-2:矩阵与变换 本题主要考查矩阵运算等基础知识,考查运算求 解能力.
【解答】 A2==.
设α=.由A2α=β,得=,从而
解得x=-1,y=2,所以α=.
N3 C.选修4-4:坐标系与参数方程 本题主要考查椭圆及直线的参数方程等基础知识,考查转化问题的能力.
【解答】 由题设知,椭圆的长半轴长a=5,短半轴长b=3,从而c==4,所以右焦点为(4,0).将已知直线的参数方程化为普通方程:x-2y+2=0.
故所求直线的斜率为,因此其方程为y=(x-4),即x-2y-4=0.
N4 D.选修4-5:不等式选讲 本题主要考查解绝对值不等式的基础知识,考查分类讨论、运算求解能力.
【解答】 原不等式可化为
或
解得≤x<或-2
查看更多