2021届课标版高考文科数学大一轮复习课件：§2-3 二次函数与幂函数（讲解部分）

2021届课标版高考文科数学大一轮复习课件：§2-3 二次函数与幂函数（讲解部分）

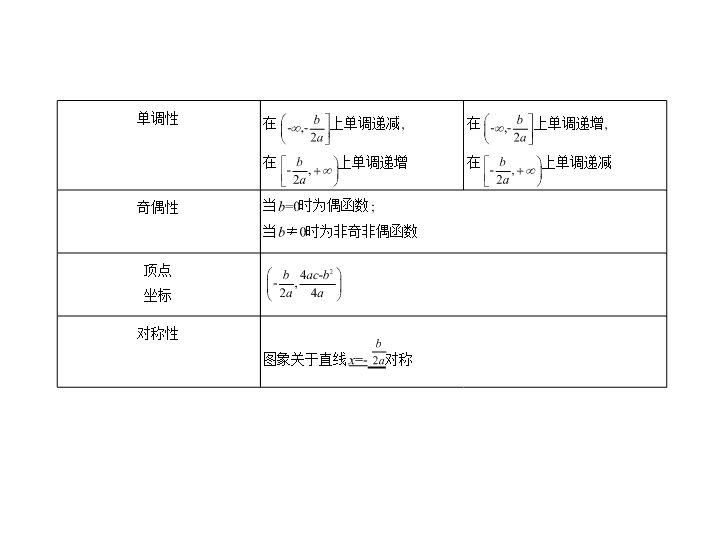
考点一　二次函数 考点清单 考向基础 1.二次函数的三种表示形式 (1)一般式: f ( x )= ax 2 + bx + c ( a ≠ 0); (2)顶点式: f ( x )= a ( x - m ) 2 + n ( a ≠ 0) ; (3)两根式: f ( x )= a ( x - x 1 )( x - x 2 )( a ≠ 0) . 解析式 f ( x )= ax 2 + bx + c ( a >0) f ( x )= ax 2 + bx + c ( a <0) 图象     定义域 R R 值域     最值 f ( x ) min =   f ( x ) max =   2.二次函数的图象和性质 单调性 在   上单调递减, 在   上单调递增 在   上单调递增, 在   上单调递减 奇偶性 当 b =0时为偶函数; 当 b ≠ 0时为非奇非偶函数 顶点 坐标   对称性 图象关于直线 x =-   对称 3.一元二次方程根的分布 设 x 1 , x 2 是实系数一元二次方程 ax 2 + bx + c =0( a >0)的两实根,则 x 1 , x 2 的分布范围 与一元二次方程系数之间的关系如下表所示: 根的分布 ( m , n , p 为常数) f ( x )= ax 2 + bx + c ( a >0) 的图象 满足条件 x 1 < x 2 < m     m < x 1 < x 2     x 1 < m < x 2   f ( m )<0 m < x 1 < x 2 < n     m < x 1 < n < x 2 < p     只有一个零点 在( m , n )之间     或 f ( m )· f ( n )<0 或   或   考向一　二次函数的最值(取值范围) 考向突破 例1    (2018广东坪山期末,8)若函数 f ( x )= x 2 -3 x -4的定义域为[0, m ],值域为   ,则 m 的取值范围是   (　　) A.(0,4]　     B.   C.   　    D.   解析　∵ f ( x )= x 2 -3 x -4=   -   ,∴ f   =-   ,又 f (0)= f (3)=-4,∴由二次函数 图象可知 m 的值最小为   ,最大为3.故 m 的取值范围是   ,故选C. 答案    C 考向二　一元二次方程的实根分布 例2　已知对于任意的 x ∈(- ∞ ,1) ∪ (5,+ ∞ ),都有 x 2 -2( a -2) x + a >0,则实数 a 的 取值范围是 　　　     . 解析　令 f ( x )= x 2 -2( a -2) x + a ,则当 Δ =4( a -2) 2 -4 a <0,即1< a <4时, f ( x )>0在R上恒 成立,符合题意;当 Δ =0时,[-2( a -2)] 2 -4 a =0, 解得 a =1或 a =4,经验证,当 a =1时不符合题意,舍去; 当 Δ >0时,[-2( a -2)] 2 -4 a >0,解得 a <1或 a >4, 此时函数 f ( x )的两个零点都在[1,5]上, 则   解得4< a ≤ 5. 综上,实数 a 的取值范围是(1,5]. 答案　(1,5] 考点二　幂函数 考向基础 1.幂函数的图象   2.幂函数的性质 考向　幂函数图象的应用 考向突破 例3    (2018鄂东南省级示范高中教育教学改革联盟联考,4)若幂函数 y = x -1 , y = x m 与 y = x n 在第一象限内的图象如图所示,则 m 与 n 的取值情况为   (　　)   A.-1< m <0< n <1　     B.-1< n <0< m C.-1< m <0< n 　     D.-1< n <0< m <1 解析　对于幂函数 y = x α ,当 α >0时, y = x α 在(0,+ ∞ )上为增函数,且0< α <1时,图 象上凸,∴0< m <1;当 α <0时, y = x α 在(0,+ ∞ )上为减函数,不妨令 x =2,根据图象 可得2 -1 <2 n ,∴-1< n <0.综上所述,-1< n <0< m <1,选D. 答案    D 方法1　 求二次函数在闭区间上的最值(值域)的方法 求二次函数最值问题,一般先用配方法化成 y = a ( x - m ) 2 + n ( a ≠ 0)的形式,得其 图象的顶点坐标为( m , n ),对称轴为直线 x = m ,再结合二次函数的图象求解,常 见的有三种类型: (1)对称轴、区间都是给定的;(2)对称轴动,区间固定;(3)对称轴定,区间变 动.解决这类问题的思路是抓住 “三点一轴” 数形结合求解,三点指的是区 间的两个端点及区间的中点,一轴指的是对称轴.具体方法是利用函数的单 调性及分类讨论的思想求解. 对于(2)、(3),通常要分对称轴在区间内、对称轴在区间外两大类情况进 行讨论. 简单地讲: 轴在区间外,端点处取最值,轴在区间内,顶点或端点处取最值. 方法技巧 例1    (2018陕西渭南尚德中学一模,20)已知函数 f ( x )= x 2 +(2 a -1) x -3. (1)当 a =2, x ∈[-2,3]时,求函数 f ( x )的值域; (2)若函数 f ( x )在[1,3]上的最大值为1,求实数 a 的值.     解析　(1)当 a =2时, f ( x )= x 2 +3 x -3=   -   , 又 x ∈[-2,3],所以 f ( x ) min = f   =-   , f ( x ) max = f (3)=15,所以所求函数的值域为   . (2)易知 f ( x )图象的对称轴为直线 x =-   . ①当-   ≤ 1,即 a ≥ -   时, f ( x ) max = f (3)=6 a +3, 所以6 a +3=1,即 a =-   ,满足题意; ②当-   ≥ 3,即 a ≤ -   时, f ( x ) max = f (1)=2 a -3, 所以2 a -3=1,即 a =2,不满足题意; ③当1<-   <3,即-   < a <-   时, f ( x ) max 在区间端点处取得,令 f (1)=1+2 a -1-3=1, 解得 a =2(舍去),令 f (3)=9+3(2 a -1)-3=1,解得 a =-   (舍去). 综上,可知 a =-   . 方法2 　一元二次方程根的分布问题的解法 研究一元二次方程根的分布问题时,常借助二次函数的图象来解,一般从 开 口方向、对称轴位置、判别式、端点函数值符号 这四个方面来分析. 例2　已知函数 f (log 2 x )= x 2 +2 x . (1)求函数 f ( x )的解析式; (2)若方程 f ( x )= a ·2 x -4在区间(0,2)内有两个不相等的实根,求实数 a 的取值范 围.   (1)令 t =log 2 x , t ∈R,使用换元法求出 f ( x )的解析式; (2)令2 x = m , m ∈(1,4),则问题转化为关于 m 的方程 m 2 +(2- a ) m +4=0在(1,4)上有 两解,然后列不等式组求出 a 的取值范围. 解题导引    解析　(1)设 t =log 2 x , t ∈R,则 x =2 t , x >0, f ( t )=2 2 t +2·2 t =4 t +2 t +1 , ∴ f ( x )=4 x +2 x +1 ( x >0). (2)∵方程 f ( x )= a ·2 x -4在区间(0,2)内有两个不相等的实根,∴4 x +(2- a )2 x +4=0 在(0,2)内有两个不相等的实根. 令2 x = m ,则 m ∈(1,4),令 h ( m )= m 2 +(2- a ) m +4, 则 h ( m )=0在(1,4)上有两个不相等的实根, ∴   解得6< a <7. 故实数 a 的取值范围是(6,7).