数学(文)卷·2017安徽省巢湖市柘皋中学高三上学期第四次月考(2016
巢湖市柘皋中学 2016-2017 年高三上第四次月考
数 学 试 卷(文)
考试时间:120分钟 满分:150分
命题人:梁小跃 审题人:王军
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分.在每题的四个选项中,只有一项
是符合要求的.
1.集合 ,集合 ,则 ( )
A. B. C. D.
2.已知命题 对于 恒有 成立;命题 奇函数 的图像必过原点,
则下列结论正确的是( )
A. 为真 B. 为真 C. 为假 D. 为真
3.复数1-i
2-i的共轭复数对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在等差数列{an}中,已知 a4=7,a3+a6=16,an=31,则 n 为( )
A.13 B.14 C. 16 D.15
5..曲线 y=sinx + ex 在点(0,1)处的切线方程是( )
A.x-3y+3=0 B.x-2y+2=0 C.2x-y+1=0 D.3x-y+1=0
6.函数 y=Asin(ωx+φ)(ω>0,|φ|≤
π
2 )的部分图象如图所示,
则函数的一个表达式为( )
A. y=4sin(
π
8 x-
π
4 ) B.y=-4sin(
π
8 x+
π
4 )
C.y=-4sin(
π
8 x-
π
4 ) D.y=4sin(
π
8 x+
π
4 )
7.若圆 的半径为 3,直径 上一点 使 , 为另一直径的两个端点,
则 ( )
A. B. C. D.
8.设 F1、F2 分别是椭圆 E:x2+y2
b2=1(0
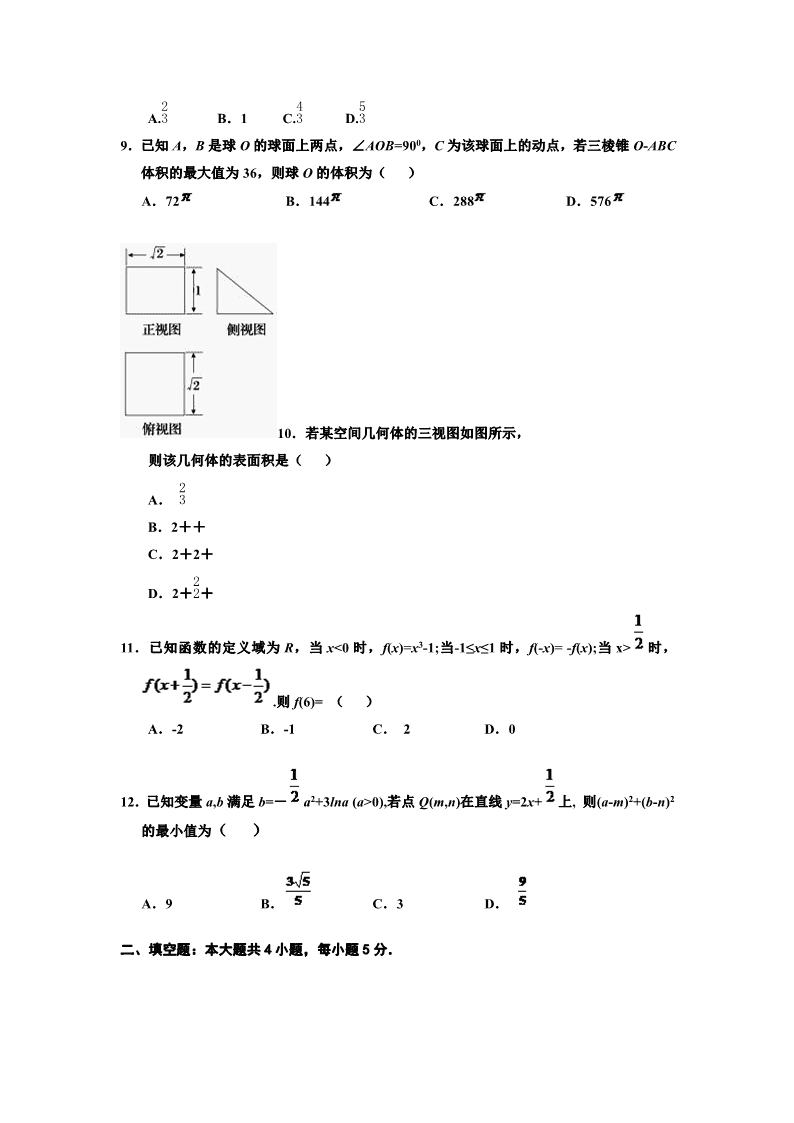
时,
.则 f(6)= ( )
A.-2 B.-1 C. 2 D.0
12.已知变量 a,b 满足 b=- a2+3lna (a>0),若点 Q(m,n)在直线 y=2x+ 上, 则(a-m)2+(b-n)2
的最小值为( )
A.9 B. C.3 D.
二、填空题:本大题共 4 小题,每小题 5 分.
13.设 x, y 满足 ,则 z=x+2y 的最大值为_________.
14.若双曲线 的右焦点与抛物线 的焦点重合,则 m=
15.已知圆 C 过点(1,0),且圆心在 x 轴的正半轴上,直线 l: 被该圆所截得的弦
长为 ,则圆 C 的标准方程为 .
16.已知函数 f(x)= .若函数 y=f(x)-a|x|恰有 4 个零点,则实数 a 的取值
范围为_______.
三、解答题:本大题共 6 小题,共 70 分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分 10 分)
已知向量 , ,f(x)= .
(1)求 f(x)的最大值和对称轴;
(2)讨论 f(x)在 上的单调性.
18.(本小题满分 12 分)
如图,某水域的两直线型岸边 l1,l2 成
定角 120o,在该水域中位于该角角平分线上且与顶点 A 相距 1 公里的 D 处有一固定桩.现
某渔民准备经过该固定桩安装一直线型隔离 BC(B,C 分别在 l1 和 l2 上),围出三角形 ABC
养殖区,且 AB 和 AC 都不超过 5 公里.设 AB=x 公里,AC=y 公里.
(1)将 y 表示成 x 的函数,并求其定义域;
(2)该渔民至少可以围出多少平方公里的养殖区?
19.(本小题满分 12 分)
已知{an}是等差数列,{bn}是等比数列,且 b2=3,b3=9, a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设 cn= an .bn,求数列{cn}的前 n 项和.
20.(本小题满分 12 分)
如图,在平面四边形 中,
,
(1)求 的值;
(2)求 的长.
21.(本小题满分 12 分)
已知函数 .
(1)当 时,求 的极值;
(2)当 时,讨论 的单调性.
22.(本小题满分 12 分)
如 图 , 在 四 棱 锥 中 , 平 面 平 面
, , , , , , .
(1)求证: 平面 ;
(2)求四棱锥 的体积;
(3)在棱 上是否存在点 ,使得 平面 ?若存在,求 的值;若不存
在,说明理由.
2017 届高三第四次月考数学(文科)参考答案
一.选择题
1 2 3 4 5 6 7 8 9 10 11 12
B D A C C B D C C C C D
二.填空题
13.7 14. 12 15. 16.(1,2)
三.解答题
17. 解:(1)f(x)=sinxcosx- cos2x=
cosxsinx- (1+cos2x)= ,
所以最大值为 , 由 2x- =k + ,k∈Z, 所以对称轴 x= , k∈
Z
(2)当 x∈ 时, 从而当 ,
时,f(x)单调递增
当 ,f(x)单调递减
综上可知 f(x)在 上单调递增,在 上单调减。
18 解:(1)由 SΔABD+SΔACD=SΔABC
得 12xsin60º+12ysin60º=12xysin120º
所以 x+y=xy,所以 y=xx-1
又 0<y≤5,0<x≤5,所以 54≤x≤5 , 所以定义域为{x|54≤x≤5}
(2)设△ABC 的面积为 S,则结合(1)易得
方法一:S=12xysinA=12x·xx-1·sin120º=3x2x-1,(54≤x≤5)
x2x-1=x-1+1x-1=(x-1)+1x-1+2≥4,
当仅当 x-1=1x-1,x=2 时取等号.
故当 x=y=2 时,面积 S 取最小值(平方公里)
方法二:S=SΔABD+SΔACD=12xsin60º+12ysin60º=34(x+xx-1)
=34(x+x-1+1x-1)=34(x+1x-1+1)
=34[(x-1)+1x-1+2]≥
当且仅当 x-1=1x-1,即 x=2 时取等号.
故当 x=y=2 时,面积 S 取最小值(平方公里)
答:该渔民总共至少可以围出平方公里的养殖区.
19.解:(I)等比数列 的公比 ,
所以 , .
设等差数列 的公差为 .
因为 , ,
所以 ,即 .
所以 ( , , , ).
(II)由(I)知, , .
因此由错位相减法得数列 的前 项和
20.如图,设
(1)在 中,由余弦定理,得
于是由题设知,
解得 ( 舍去)
在 中,由正弦定理,得
于是,
(2)由题设知, ,于是由(1)知,
而 ,所以
在 中, ,所以
21.【解】(Ⅰ)当 时, ,定义域为 ,
的导函数 .
当 时, , 在 上是减函数;
当 时, , 在 上是增函数.
∴当 时, 取得极小值为 ,无极大值.
(Ⅱ)当 时, 的定义域为 , 的导函数为
.
由 得 , , .
(1)当 时, 在 上是减函数,在 上是增函数,在
上是减函数;
(2)当 时, 在 上是减函数;
(3)当 时, 在 上是减函数,在 上是增函数,在 上是
减函数.
综上所述,
当 时, 在 上是减函数,在 上是增函数;
当 时, 在 上是减函数;
当 时, 在上是减函数,在 上是增函数.
22、【答案】(1)见解析;(2);(3)存在,
【解析】
试题解析:(1)因为平面 平面 , ,
所以 平面 ,所以 ,
又因为 ,所以 平面 ;