- 2021-07-01 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年高考数学(理)二轮复习讲练测 专题15 分段函数的性质、图象以及应用(讲)(解析版)
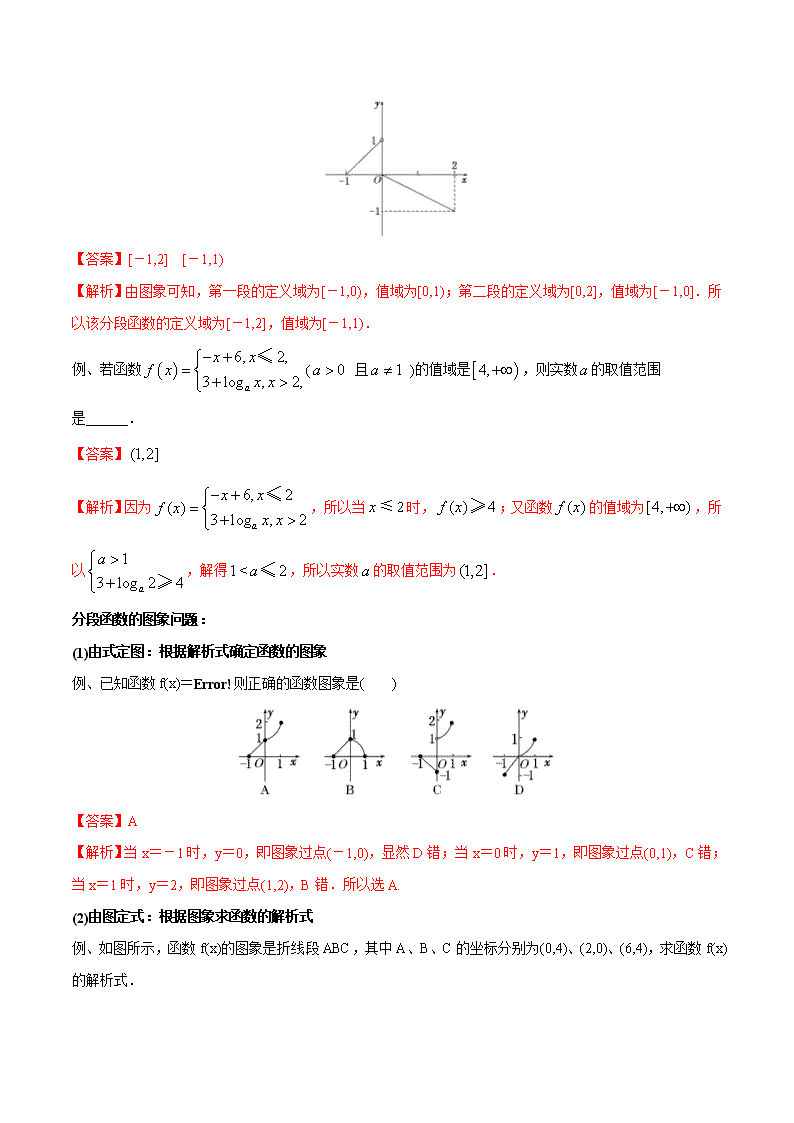
专题15 分段函数的性质、图象以及应用 新课标下高考数学题中以分段函数为载体,考查函数的图像、性质等知识的习题倍受青睐.所谓的分段函数是指自变量X在不同的取值范围内对应关系不同的函数,由分段函数本身的特点,使得一个函数在各段上有不同的解析式,所以可将一次函数、反比例函数、二次函数、指数函数、对数函数、三角函数、抽象函数融合在一个题目之中,考查多个知识点.因而分段函数已成为高考命题的一个热点.纵观近几年高考对于分段函数的性质、图象的考查,重点放在函数的奇偶性、周期性以及函数的零点问题与分段函数结合上;要求学生有较强的抽象思维能力、作图能力以及准确的计算能力,才能顺利解答.从实际教学来看,这部分知识是学生掌握比较模糊,看到就头疼的题目.分析原因,除了这类题目本身就是压轴题确实不易之外,主要是学生的作图能力普遍较弱,还有就是没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理. 本文就高中阶段出现这类问题加以类型的总结和方法的探讨. 知识储备: 分段函数:定义域中各段的与的对应法则不同,函数式是分两段或几段给出的.分段函数是一个函数,定义域、值域都是各段的并集.分段函数中的问题一般是求解析式、值域或最值,讨论奇偶性、单调性等.分段函数的处理方法:分段函数分段研究. 分段函数的函数值问题: (1)已知自变量求函数值 例、已知函数=,若=4,则实数= A. B. C.2 D.9 【答案】C 【解析】∵,∴.于是,由得 .故选. 例、设,则的值为 A.1 B.0 C. D. 【答案】B 【解析】∵π是无理数 ∴g(π)=0 则=f(0)=0 ,故选B. 例、函数满足,且在区间上,则的值为 . 【答案】 【解析】因为函数满足(),所以函数的最小正周期是4.因为在区间 上,,所以. (2)已知函数值求自变量: 已知函数值求自变量或其它参数的值的问题,一般按自变量的取值范围分类讨论,通过解方程而得到.数形结合是解答此类问题的重要方法. 例、已知函数.若,则实数的值等于 A.-3 B.-1 C.1 D.3 【答案】A 【解析】当时,由得,无解;当时,由得,解得,故选A. 例、已知函数f(x)=且f(a)=-3,则f(6-a)=( ) A.- B.- C.- D.- 【答案】A 【解析】因为f(x)=f(a)=-3,所以或 解得a=7,所以f(6-a)=f(-1)=2-1-1-2=-,选A. 分段函数的定义域值域问题: 例、如图为一分段函数的图象,则该函数的定义域为________,值域为________. 【答案】[-1,2] [-1,1) 【解析】由图象可知,第一段的定义域为[-1,0),值域为[0,1);第二段的定义域为[0,2],值域为[-1,0].所以该分段函数的定义域为[-1,2],值域为[-1,1). 例、若函数( 且 )的值域是,则实数的取值范围是 . 【答案】 【解析】因为,所以当时,;又函数的值域为,所以,解得,所以实数的取值范围为. 分段函数的图象问题: (1)由式定图:根据解析式确定函数的图象 例、已知函数f(x)=则正确的函数图象是( ) 【答案】A 【解析】当x=-1时,y=0,即图象过点(-1,0),显然D错;当x=0时,y=1,即图象过点(0,1),C错;当x=1时,y=2,即图象过点(1,2),B错.所以选A. (2)由图定式:根据图象求函数的解析式 例、如图所示,函数f(x)的图象是折线段ABC,其中A、B、C的坐标分别为(0,4)、(2,0)、(6,4),求函数f(x)的解析式. 【答案】f(x)= 【解析】设线段AB所对应的函数解析式为y=kx+b, 将与代入,得 ∴∴y=-2x+4(0≤x≤2). 同理,线段BC所对应的函数解析式为y=x-2(2查看更多