【数学】2018届一轮复习人教A版　正弦定理与余弦定理学案

【数学】2018届一轮复习人教A版　正弦定理与余弦定理学案

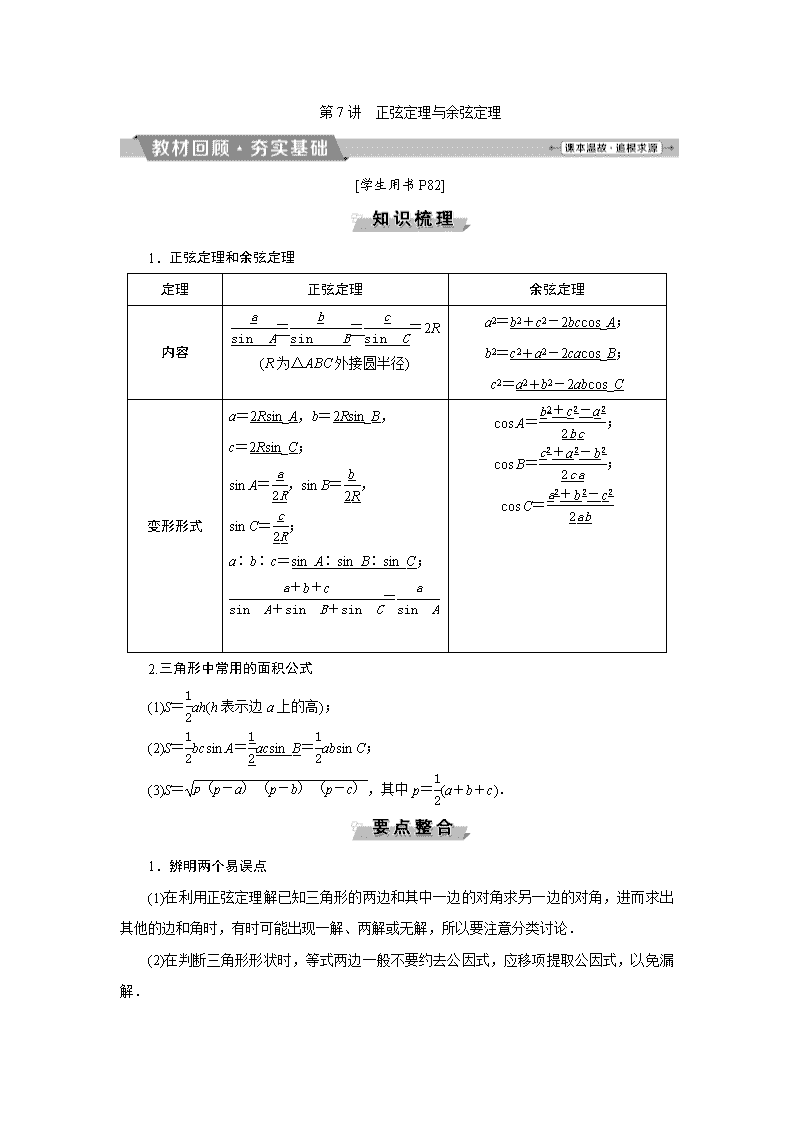
第7讲　正弦定理与余弦定理 ‎ [学生用书P82]‎ ‎1．正弦定理和余弦定理 定理 正弦定理 余弦定理 内容 ＝＝＝2R ‎(R为△ABC外接圆半径)‎ a2＝b2＋c2－2bccos_A；‎ b2＝c2＋a2－2cacos_B；‎ c2＝a2＋b2－2abcos_C 变形形式 a＝2Rsin_A，b＝2Rsin_B，‎ c＝2Rsin_C；‎ sin A＝，sin B＝，‎ sin C＝；‎ a∶b∶c＝sin_A∶sin_B∶sin_C；‎ ＝ cos A＝；‎ cos B＝；‎ cos C＝ ‎2.三角形中常用的面积公式 ‎(1)S＝ah(h表示边a上的高)；‎ ‎(2)S＝bcsin A＝acsin_B＝absin C；‎ ‎(3)S＝，其中p＝(a＋b＋c)．‎ ‎1．辨明两个易误点 ‎(1)在利用正弦定理解已知三角形的两边和其中一边的对角求另一边的对角，进而求出其他的边和角时，有时可能出现一解、两解或无解，所以要注意分类讨论．‎ ‎(2)在判断三角形形状时，等式两边一般不要约去公因式，应移项提取公因式，以免漏解．‎ ‎2．余弦定理的推导过程 如图，设＝a，＝b，‎ ＝c.‎ 则c＝a－b，‎ 所以|c|2＝(a－b)2‎ ‎＝a2－2a·b＋b2‎ ‎＝|a|2＋|b|2－2|a||b|cos C.‎ 即c2＝a2＋b2－2abcos C.‎ 同理可证a2＝b2＋c2－2bccos A.‎ b2＝c2＋a2－2cacos B.‎ ‎3．三角形解的判断 A为锐角 A为钝角或直角 图形 关系式 a＝bsin A bsin Ab 解的个数 一解 两解 一解 一解 ‎1. 在△ABC中，A＝45°，C＝30°，c＝6，则a等于(　　)‎ A．3　　　　　　　　 B．6 C．2 D．3 ‎　B　[解析] 由正弦定理得＝，‎ 所以a＝＝＝6.‎ ‎2. 在△ABC中，已知a＝5，b＝7，c＝8，则A＋C＝(　　)‎ A．90° B．120°‎ C．135° D．150°‎ ‎　B　[解析] cos B＝＝＝.‎ 所以B＝60°，所以A＋C＝120°.‎ ‎3．在△ABC中，若a＝18，b＝24，A＝45°，则此三角形(　　)‎ A．无解 B．有两解 C．有一解 D．解的个数不确定 ‎　B　[解析] 因为＝，‎ 所以sin B＝·sin A＝×sin 45°‎ ‎＝.‎ 又因为a

查看更多