数学理卷·2018届四川省成都实验高级中学高三12月月考（2017

数学理卷·2018届四川省成都实验高级中学高三12月月考（2017

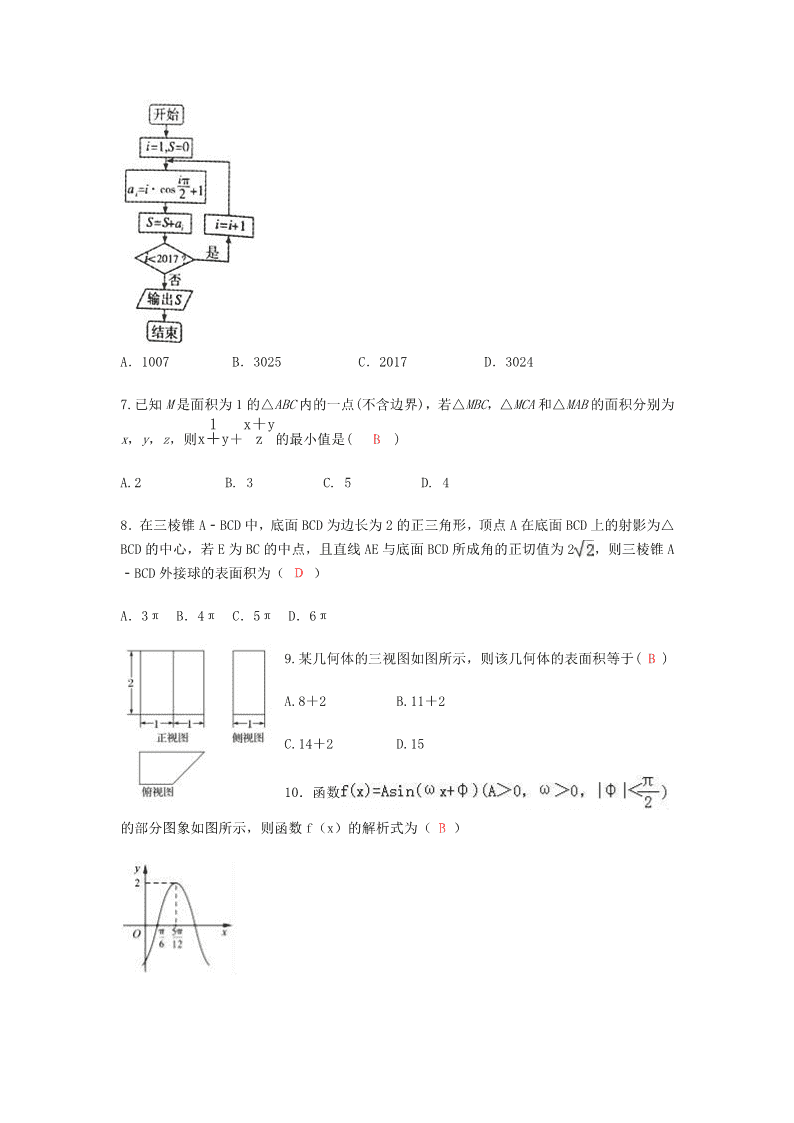
成都实验高级中学 2015 级高三上学期 12 月月考试题 数 学（理科） 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中，只有一 项是符合题目要求的. 1．已知集合 ， ，则 的真子集个 数为（ B ） A．1 B．3 C．4 D．7 2.设 ，其中 为虚数单位， ， 是实数，则 （ D ） A．1 B． C． D． 3. 已知 ， ， ，则（ A ） A. B. C. D. 【解析】由题意得 ， ， ， ∴ 。选 A。 4.对于实数 ，“ ”是“ ”的（ B ） A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 5.如图是某高三学生七次模拟考试的物理成绩的茎叶图，则该学生物 理成绩的平均数和中位数分别为( B ) A.87 和 85 B.86 和 85 C.87 和 84 D.86 和 84 6.某程序框图如图所示，该程序运行后输出的 的值是（ B ） A．1007 B．3025 C．2017 D．3024 7.已知 M 是面积为 1 的△ABC 内的一点(不含边界)，若△MBC，△MCA 和△MAB 的面积分别为 x，y，z，则 1 x＋y＋ x＋y z 的最小值是( B ) A.2 B. 3 C. 5 D. 4 8．在三棱锥 A﹣BCD 中，底面 BCD 为边长为 2 的正三角形，顶点 A 在底面 BCD 上的射影为△ BCD 的中心，若 E 为 BC 的中点，且直线 AE 与底面 BCD 所成角的正切值为 2 ，则三棱锥 A ﹣BCD 外接球的表面积为（ Ｄ ） A．3π B．4π C．5π D．6π 9.某几何体的三视图如图所示，则该几何体的表面积等于( B ) A.8＋2 B.11＋2 C.14＋2 D.15 10．函数 的部分图象如图所示，则函数 f（x）的解析式为（ B ） A． B． C． D． 11.已知直线 分别与直线 及曲线 交于 ， 两点， 则 ， 两点间距离的最小值为 D A. B.3 C. D. 12.对于三次函数 ，给出定义：设 是函数 的导 数， 是函数 的导数，若方程 有实数解 ，则称点 为函数 的“拐点”。经过探究发现：任何一个三次函数都有“拐点”和对称中心，且“拐 点”就是对称中心。设函数 ，则 （ B ） ． ． ． ． 二、填空题：（本大题共 4 小题，每小题 5 分。共 20 分） 13． . 13． ； 14.已知向量 ， 满足 ， ， ，则 ．14. 15.在 中， ， ，若最大边长为 63，则最小边为 ．15.25 16. 设函数 ， 是由 轴和曲线 及该曲线在点 处 的切线所围成的封闭区域，则 在 上的最小值为 . 16. 三、解答题 （本大题共 6 小题，共 70 分．解答应写出文字说明、证明过程或演算步骤．） 17. （本题满分 12 分） 已知等差数列 的前 项和为 ，且 的首项与公差相同，且 . （Ⅰ）求数列 的通项公式以及前 项和为 的表达式； （Ⅱ）若 ，求数列 的前 项和 . 17.【答案】（1） , （2） 【解析】试题分析：（Ⅰ）由数列 的首项与公差相同且 可得 ，从而可求 得数列的通项公式和前 项和公式；（Ⅱ）由条件得 ，可采用分组求和、裂 项求和的方法求解即可。 【解析】：（Ⅰ）依题意得 解得 ； ∴ ， . （Ⅱ）依题意得： ， ∴ . 18.（本题满分 12 分） 如图，在四棱锥 中， 平面 ，底面 是菱形， ， ． （Ⅰ）求证：平面 平面 ； （Ⅱ）若 ，求 与平面 所成角的正弦值． 18.（Ⅰ）证明：∵四边形 是菱形，∴ . 又∵ 平面 ， 平面 ，∴ ． 又 ， 平面 ， 平面 ，∴ 平面 ， ∵ 平面 ，∴平面 平面 . （Ⅱ）解：设 ，因为 ， ，所以 ， ，如图，以 为坐标原点，建立空间直角坐标系 ，则 ， ， ， ， ，所以 ， ， . 设平面 的法向量为 ，则 则 解得 ， 令 ，得 ，∴ ． 设 与平面 所成角为 ，则 ， 则 与平面 所成角的正弦值为 ． 19.（本小题满分 12 分） 王明参加某卫视的闯关活动，该活动共 3 关．设他通过第一关的概率为 0. 8，通过第二、 第三关的概率分别为 p，q，其中 ，并且是否通过不同关卡相互独立．记ξ为他通过的 关卡数，其分布列为： ξ 0 1 2 3 P 0. 048 a b 0. 192 （Ⅰ）求王明至少．．通过 1 个关卡的概率； （Ⅱ）求 p，q 的值． 19.（本小题满分 12 分） 解：（Ⅰ）设事件 表示“王明通过第 i 个关卡”，由题意知 ， ， ． …………………… 2 分 由于事件“王明至少通过 1 个关卡”与事件“ξ＝0”是对立的，所以王明至少通过 1 个关卡的概率是 ． …………………………… 6 分 （Ⅱ）由题意 ， ． 整理得 ， ，又 ，所以 ， ． ………… 12 分 20.（本小题满分 12 分） 如图，已知直线 过椭圆 的右焦点 ，抛物线： 的焦点为椭圆 的上顶点，且直线 交椭圆 于 两点，点 在直线 上的射影依次为点 ． （Ⅰ）求椭圆 的方程； （Ⅱ）若直线 交 轴于点 ，且 ，当 变化时，探求 的值是否为定值？若是，求出 的值，否则，说明理由. 20.（本题满分 12 分） 解：（Ⅰ）易知椭圆右焦点 F（1，0），∴c=1， 抛物线 的焦点坐标 ，∴ ∴b2=3 ∴a2=b2+c2=4∴椭圆 C 的方程 （Ⅱ）易知 m≠0，且 l 与 y 轴交于 ， 设直线 l 交椭圆于 A（x1，y1），B（x2，y2） 由 ∴△=（6m）2+36（3m2+4）=144（m2+1）＞0 ∴ 又由 ∴ 同理 ∴ ∵ ∴ 所以，当 m 变化时，λ1+λ2 的值为定值 。 21.（本小题满分 12 分） 已知过点 ， 且圆心在直线 上的圆 与 轴相交于 两点，曲线 上 的任意一点 与 两点连线的斜率之积为 ． （Ⅰ）求曲线 的方程； （Ⅱ）过原点 作射线 ， ，分别平行于 ， ，交曲线 于 ， 两点， 求 的取值范围． 21．本题主要考查直线、圆、椭圆、直线与椭圆的位置关系等基础知识，考查运算求解能力、 推理论证能力，考查函数与方程思想、化归与转化思想，考查考生分析问题和解决问题的能 力，满分 12 分． 解法一：（Ⅰ）∵圆 过点 ， ， ∴圆心在直线 上，……………………………………………………1 分 又圆心在直线 上， ∴当 时， ，即圆心为 .……………………………………2 分 又 与 的距离为 ， ∴圆 的方程为 .……………………………………………3 分 令 ，得 . ……………………………………………………………4 分 不妨设 ， ， 由题意可得 ， ， ∴ , ∴曲线 的方程为： ( )．………………………………6 分 （Ⅱ）设 ，射线 的斜率为 ，则射线 的斜率为 . 解得 ………………………7 分 ∴ ．………………………8 分 同理， …9 分 ∴ ． 设 ，则 ， ∴ ，………………………………10 分 又∵ ， ∴ .………………………………………………………………12 分 解法二：（Ⅰ）同解法一； （Ⅱ）设 ，射线 的斜率为 ，则射线 的斜率为 . 解得 ………………………………………………7 分 ∴ ．………………………………………………8 分 同理 ，……………………………9 分 ∴ ……………………………10 分 ………………………………………………………11 分 即 ．………………………………………………………12 分 请考生在 22、23 两题中任选一题作答，如果多做，则按所做的第一题记分． 22. 选修 4-4：坐标系与参数方程 已知曲线 的参数方程为 （ 为参数）以原点为极点， 轴正半轴为极轴建立 极坐标系. （Ⅰ）求曲线 的极坐标方程； （Ⅱ）若直线 交曲线 于 两点，求 . 22.【答案】（1） （2） 【解析】试题分析：（Ⅰ）将曲线 的参数方程消去参数即可得到普通方程 ，再将将 代入普通方程可得极坐标方程为 ； （Ⅱ）根据条件可求得直线的直角坐标方程为 ，由圆的弦长的求法可得弦长。 试题解析： （Ⅰ）∵曲线 的参数方程为 （ 为参数） ∴曲线 的普通方程为 曲线 表示以 为圆心， 为半径的圆. 将 代入并化简得： 即曲线 的极坐标方程为 . （Ⅱ）∵ ， ∴ ， 可得直线的直角坐标方程为 ； ∴圆心 到直线的距离为 ∴弦长为 . 23.(本题满分 10 分)选修 4—5: 不等式选讲 设 f(x)＝|x－1|＋|x＋1|. (Ⅰ)求 f(x)≤x＋2 的解集； (Ⅱ)若不等式 f(x)≥ |a＋1|－|2a－1| |a| 对任意实数 a≠0 恒成立，求实数 x 的取值范围． 23.【解析】(Ⅰ)由 f(x)≤x＋2 得： x≤－1， 1－x－x－1≤x＋2，或 －1

查看更多