平面与平面垂直的判定教案2

平面与平面垂直的判定教案2

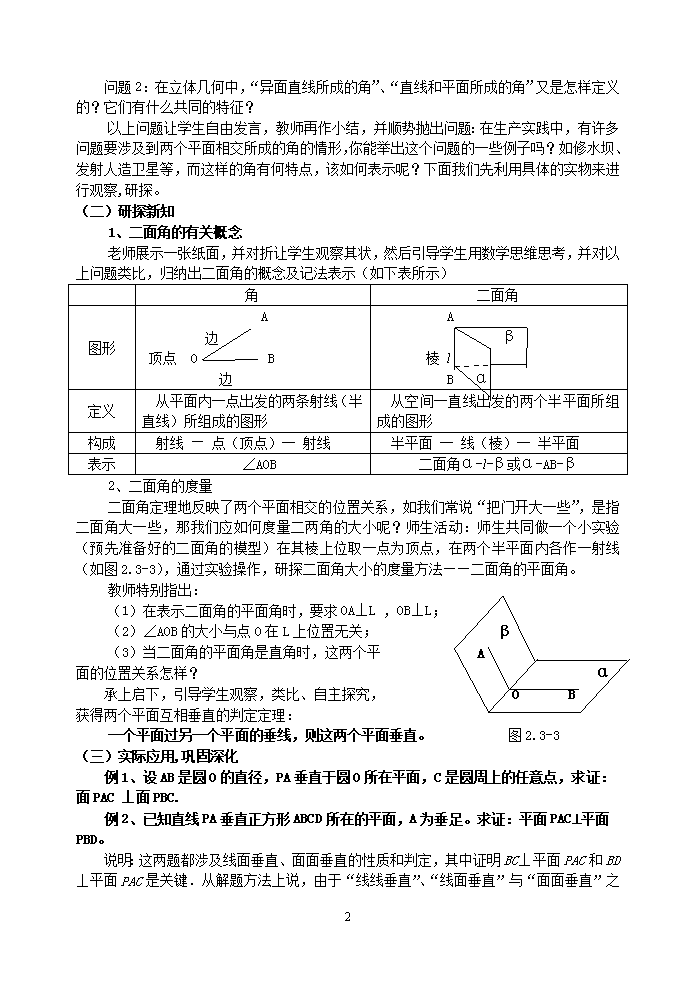
‎ ‎ ‎《2.3.2平面与平面垂直的判定》教学设计 教学内容 人教版新教材 高二数学 第二册 第二章 第三节 第2课 教材分析 ‎ 直线与平面垂直问题是直线与平面的重要内容，也是高考考查的重点，求解的关键是根据线与面之间的互化关系，借助创设辅助线与面，找出符号语言与图形语言之间的关系把问题解决。通过对有关概念和定理的概括、证明和应用，使学生体会“转化”的观点，提高学生的空间想象力和逻辑推理能力。‎ 学情分析 ‎1.学生思维活跃，参与意识、自主探究能力较强，故采用启发、探究式教学。‎ ‎2.学生的抽象概括能力和空间想象力有待提高，故采用多媒体辅助教学。‎ 教学目标 ‎1.知识与技能 ‎（1）使学生正确理解和掌握“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念；‎ ‎（2）使学生掌握两个平面垂直的判定定理及其简单的应用；‎ ‎（3）使学生理会“类比归纳”思想在数学问题解决上的作用。‎ ‎（4）通过实例让学生直观感知“二面角”概念的形成过程；‎ ‎（5）类比已学知识，归纳“二面角”的度量方法及两个平面垂直的判定定理。‎ ‎2.情感态度与价值观 ‎（1）培养学生的几何直观能力，使他们在直观感知，操作确认的基础上学会归纳.‎ ‎（2）发展学生的合情推理能力和空间想象力 ，培养学生的质疑思辨、创新的精神.‎ ‎（3）让学生亲身经历数学研究的过程，体验探索的乐趣，增强学习数学的兴趣.‎ 教学重、难点 ‎1.重点：平面与平面垂直的判定。‎ ‎2.难点：找出二面角的平面角。‎ 教学理念 学生是学习和发展的主体，教师是教学活动的组织者和引导者. ‎ 设计思路：‎ 通过“直观感知、操作确认，推理证明”，培养学生空间概念、空间想象能力以及逻辑推理能力。让学生在观察物体模型的基础上，进行操作确认，获得对性质定理正确性的认识；“二面角”、“二面角的平面角”及“直二面角”、“两个平面互相垂直”的概念认识；利用框图对本章知识进行系统的小结，直观、简明再现所学知识，化抽象学习为直观学习，易于识记；同时凸现数学知识的发展和联系。通过揭示概念的形成、发展和应用过程，使学生理会教学存在于观实生活周围，从中激发学生积极思维，培养学生的观察、分析、解决问题能力。‎ 教学过程：‎ ‎（一）创设情景，揭示课题 问题1：平面几何中“角”是怎样定义的？‎ 3‎ ‎ ‎ 问题2：在立体几何中，“异面直线所成的角”、“直线和平面所成的角”又是怎样定义的？它们有什么共同的特征？‎ 以上问题让学生自由发言，教师再作小结，并顺势抛出问题：在生产实践中，有许多问题要涉及到两个平面相交所成的角的情形，你能举出这个问题的一些例子吗？如修水坝、发射人造卫星等，而这样的角有何特点，该如何表示呢？下面我们先利用具体的实物来进行观察,研探。‎ ‎（二）研探新知 ‎1、二面角的有关概念 老师展示一张纸面，并对折让学生观察其状，然后引导学生用数学思维思考，并对以上问题类比，归纳出二面角的概念及记法表示（如下表所示）‎ 角 二面角 图形 ‎ A ‎ 边 ‎ ‎ 顶点 O B ‎ 边 A ‎ ‎ β ‎ 棱 l ‎　B 　α 定义 从平面内一点出发的两条射线（半直线）所组成的图形 从空间一直线出发的两个半平面所组成的图形 构成 射线 — 点（顶点）一 射线 半平面 一 线（棱）一 半平面 表示 ‎∠AOB 二面角α-l-β或α-AB-β ‎2、二面角的度量 二面角定理地反映了两个平面相交的位置关系，如我们常说“把门开大一些”，是指二面角大一些，那我们应如何度量二两角的大小呢？师生活动：师生共同做一个小实验（预先准备好的二面角的模型）在其棱上位取一点为顶点，在两个半平面内各作一射线（如图2.3-3），通过实验操作，研探二面角大小的度量方法——二面角的平面角。‎ B A O β α 教师特别指出：‎ ‎（1）在表示二面角的平面角时，要求OA⊥L ，OB⊥L；‎ ‎（2）∠AOB的大小与点O在L上位置无关；‎ ‎（3）当二面角的平面角是直角时，这两个平 面的位置关系怎样？‎ 承上启下，引导学生观察，类比、自主探究， ‎ 获得两个平面互相垂直的判定定理：‎ 一个平面过另一个平面的垂线，则这两个平面垂直。 图2.3-3 ‎ ‎（三）实际应用,巩固深化 ‎ 例1、设AB是圆O的直径，PA垂直于圆O所在平面，C是圆周上的任意点，求证：面PAC ⊥面PBC.‎ 例2、已知直线PA垂直正方形ABCD所在的平面，A为垂足。求证：平面PAC^平面PBD。‎ 说明：这两题都涉及线面垂直、面面垂直的性质和判定，其中证明BC⊥平面PAC和BD⊥平面PAC是关键．从解题方法上说，由于“线线垂直”、“线面垂直”与“面面垂直”‎ 3‎ ‎ ‎ 之间可以相互转化，因此整个解题过程始终沿着“线线垂直线面垂直面面垂直”转化途径进行．‎ ‎（四）运用反馈，深化巩固 ‎1. 课本P.77的探究问题 ‎2. 课本P.77的练习 做法：学生思考（或分组讨论），老师与学生对话完成。‎ ‎（五）小结归纳，整体认识 ‎（1）二面角以及平面角的有关概念；‎ ‎（2）两个平面垂直的判定定理的内容，它与直线与平面垂直的判定定理有何关系？‎ ‎（六）课后巩固，拓展思维 P81习题 2.3 A组 第4、6、7题, B组 第1题 3‎