高中数学常见题型解法归纳及反馈检测 第11讲函数模型及其应用(3)

高中数学常见题型解法归纳及反馈检测 第11讲函数模型及其应用(3)

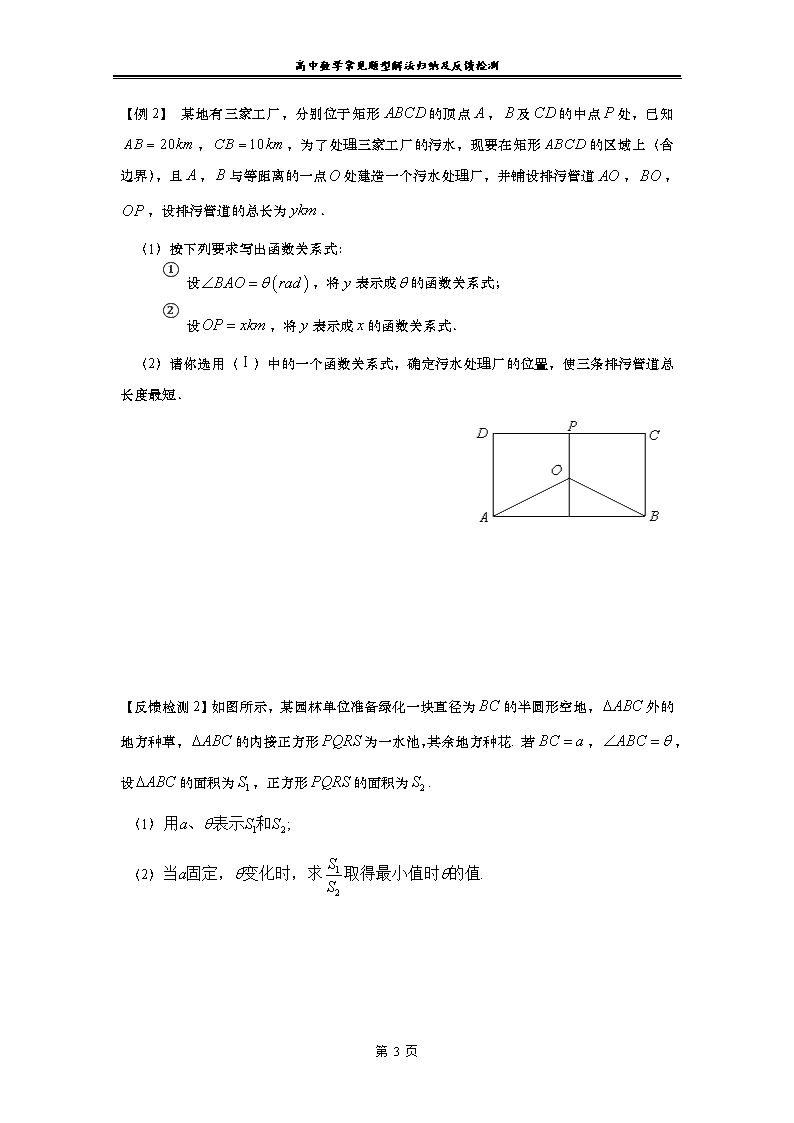
高中数学常见题型解法归纳及反馈检测 第11讲函数模型及其应用(3)‎ ‎【知识要点】‎ 一、三角函数的应用 一般是先根据题意建立三角函数模型 ，再根据题意结合三角函数的图像和性质分析解答.一般根据函数的最值确定和，根据函数的最小正周期确定，根据函数的最值点确定.‎ 二、数列的应用 三、解决实际问题的解题过程 ‎（1）对实际问题进行抽象概括：研究实际问题中量与量之间的关系，确定变量之间的主、被动关系，并用、分别表示问题中的变量；‎ ‎（2）建立函数模型：将变量表示为的函数，在中学数学内，我们建立的函数模型一般都是函数的解析式；‎ ‎（3）求解函数模型：根据实际问题所需要解决的目标及函数式的结构特点正确选择函数知识求得函数模型的解，并还原为实际问题的解.‎ 这些步骤用框图表示：‎ 四、解应用题的一般程序 ‎（1）读：阅读理解文字表达的题意，分清条件和结论，理顺数量关系，这一关是基础；‎ ‎（2）建：将文字语言转化为数学语言，利用数学知识，建立相应的数学模型．熟悉基本数学模型，正确进行建“模”是关键的一关；‎ ‎（3）解：求解数学模型，得到数学结论.一要充分注意数学模型中元素的实际意义，更要注意巧思妙作，优化过程；‎ ‎（4）答：将数学结论还原给实际问题的结果．学.科.网 第 4 页 高中数学常见题型解法归纳及反馈检测 ‎【方法讲评】‎ 函数的模型1 三角函数模型 解题步骤 先建立对应的三角函数模型，再解答.‎ ‎【例1】已知某海滨浴场的海浪高度（单位：米）与时间 （单位：时）的函数关系记作，下表是某日各时的浪高数据：‎ ‎(时)‎ ‎0‎ ‎3‎ ‎6‎ ‎9‎ ‎12‎ ‎15‎ ‎18‎ ‎21‎ ‎24‎ ‎(米)‎ ‎1.5‎ ‎1.0‎ ‎0.5‎ ‎1.0‎ ‎1.5‎ ‎1.0‎ ‎0.5‎ ‎1.0‎ ‎1.5‎ 经长期观测，的曲线可近似地看成是函数.‎ ‎（1）根据以上数据，求函数的最小正周期，振幅及函数表达式；‎ ‎（2）依据规定，当海浪高度高于1米时才对冲浪爱好者开放，请依据（1）的结论，判断一天内的上午8∶00时至晚上20∶00时之间，有多少时间可供冲浪者进行运动？‎ ‎ ‎ ‎【反馈检测1】海水受日月的引力，在一定的时候发生涨落的现象叫潮．一般地，早潮叫潮，晚潮叫汐．在通常情况下，船在涨潮时驶进航道，靠近码头；卸货后，在落潮时返回海洋．下面是某港口在某季节每天从0时至24时的时间（单位：时）与水深（单位：米）的关系表：‎ x ‎0:00‎ ‎3:00‎ ‎6:00‎ ‎9:00‎ ‎12:00‎ ‎15:00‎ ‎18:00‎ ‎21:00‎ ‎24:00‎ y ‎12.0‎ ‎15.0‎ ‎12.0‎ ‎9.0‎ ‎12.0‎ ‎15.0‎ ‎12.0‎ ‎9.0‎ ‎12.0‎ （1） 请选用一个函数来近似描述这个港口的水深与时间的函数关系； （2）一条货轮的吃水深度（船体最低点与水面的距离）为12米，安全条例规定船体最低点与洋底间隙至少要有1.5米，请问该船何时能进出港口？在港口最多能停留多长时间？‎ 第 4 页 高中数学常见题型解法归纳及反馈检测 ‎【例2】 某地有三家工厂，分别位于矩形的顶点，及的中点处，已知，，为了处理三家工厂的污水，现要在矩形的区域上（含边界），且，与等距离的一点处建造一个污水处理厂，并铺设排污管道，，，设排污管道的总长为．‎ ‎（1）按下列要求写出函数关系式：‎ ‎① 设，将表示成的函数关系式；‎ ‎② 设，将表示成的函数关系式．‎ ‎（2）请你选用（Ⅰ）中的一个函数关系式，确定污水处理厂的位置，使三条排污管道总长度最短．‎ ‎【反馈检测2】如图所示，某园林单位准备绿化一块直径为的半圆形空地，外的地方种草，的内接正方形为一水池，其余地方种花. 若，，设的面积为，正方形的面积为.‎ （1） （2） 第 4 页 高中数学常见题型解法归纳及反馈检测 函数的模型2 数列模型 解题步骤 先建立数列模型，再解答.‎ ‎【例3】 某城市2001年末汽车保有量为30万辆，预计此后每年报废上一年末汽车保有量的6%，并且每年新增汽车数量相同.为保护城市环境，要求该城市汽车保有量不超过60万辆，那么每年新增汽车数量不应超过多少辆?‎ ‎【例4】 广州市某通讯设备厂为适应市场需求，提高效益，特投入98万元引进世界先进设备奔腾6号，并马上投入生产，第一年需要的各种费用是12万元，从第二年开始，所需费用会比上一年增加4万元，而每年因引进该设备可获得的年利润为50万元.‎ ‎（1）引进该设备多少年后，开始盈利？‎ ‎（2）引进该设备若干年后，有两种处理方案：‎ 第一种：年平均盈利达到最大值时，以26万元的价格卖出；‎ 第二种：盈利总额达到最大值时，以8万元的价格卖出.问哪种方案较为合算？并说明理由.‎ ‎【反馈检测3】某企业2006年的纯利润为500万元，因设备老化等原因，企业的生产能力将逐年下降.若不能进行技术改造，预测从2007年起每年比上一年纯利润减少20万元，今年初该企业一次性投入资金600万元进行技术改造，预测在未扣除技术改造资金的情况下，第年（今年为第一年）的利润为万元（为正整数）.（Ⅰ）设从今年起的前年，若该企业不进行技术改造的累计纯利润为万元，进行技术改造后的累计纯利润为万元（须扣除技术改造资金），求、的表达式；（Ⅱ）依上述预测，从今年起该企业至少经过多少年，进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润？‎ 第 4 页