2018-2019学年江苏省海安高级中学高二10月月考数学试题 Word版

2018-2019学年江苏省海安高级中学高二10月月考数学试题 Word版

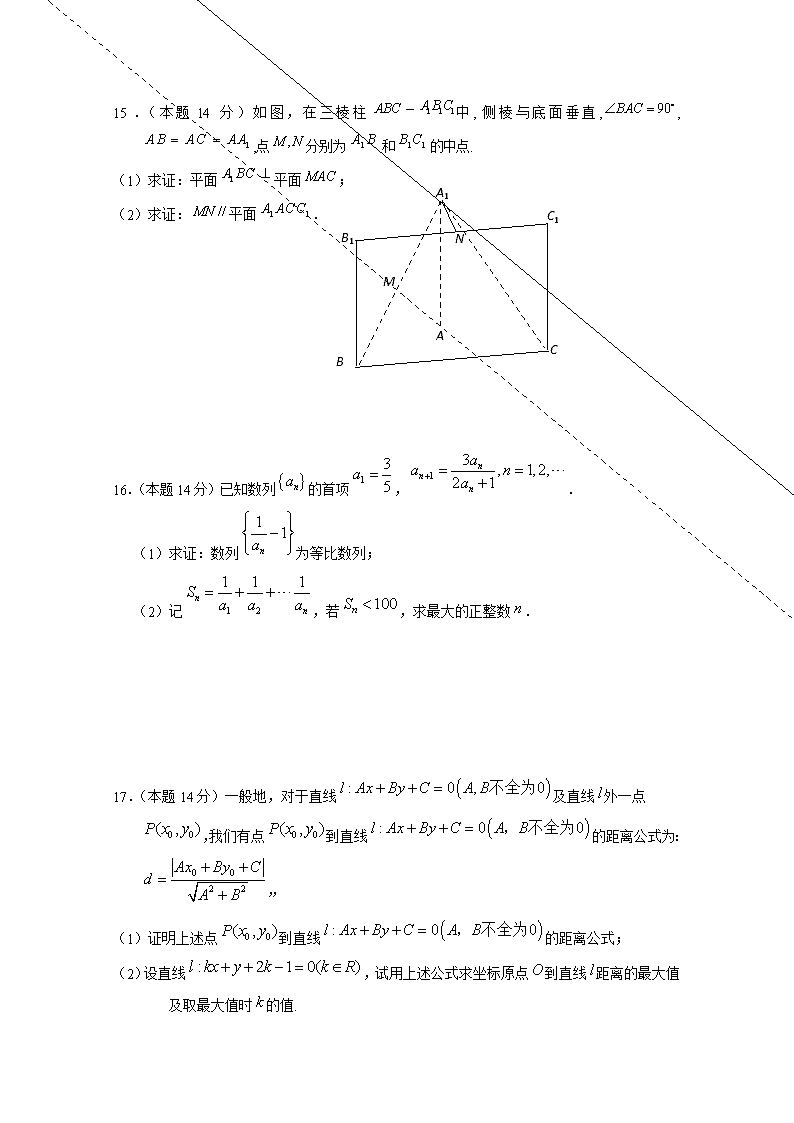
‎2018-2019学年江苏省海安高级中学高二10月月考数学试卷 一、填空题：（本大题共14小题，每小题5分，共70分．）‎ ‎1．函数的值域是 ▲ ．‎ ‎2．若直线的倾斜角为钝角，则实数的取值范围是 ▲ ．‎ ‎3．若变量满足条件，则的最大值为 ▲ ．‎ ‎4．在直角坐标系中，已知点为椭圆上的一点，且点与椭圆的两个焦点、的距离之和为6，则椭圆的标准方程为 ▲ ．‎ O A B C ‎（第7题图）‎ ‎5．设数列{}是公差不为0的等差数列，S为数列前n项和，若，，则的值为 ▲ ．‎ ‎6．已知正数满足，则的最小值为 ▲ ．‎ ‎7．在△OAC中，B为AC的中点，若，则x- y = ▲ ．‎ ‎8．已知光线通过点，被直线：反射，反射光线通过点 ‎，则反射光线所在直线的方程是 ▲ ．‎ ‎9．函数的定义域为 ▲ ．‎ ‎10．过点C(3,4)且与轴，轴都相切的两个圆的半径分别为，则= ▲ ．‎ ‎11．在平面直角坐标系中，点，若在圆上存在点P使得，则实数的取值范围是 ▲ ．‎ ‎12．已知变量，则的最小值为 ▲ ．‎ ‎13．已知圆：，为坐标原点，若正方形的一边为圆的一条弦，则线段长度的最大值是 ▲ ．‎ ‎14．若的三边长满足，则的取值范围为 ‎ ▲ ．‎ 二．本大题共6小题，共计90，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤.‎ ‎15．（本题14分）如图，在三棱柱中,侧棱与底面垂直,,,点分别为和的中点.‎ A M A1‎ C B B1‎ C1‎ N ‎（1）求证：平面平面；‎ ‎（2）求证：平面．‎ ‎16．（本题14分）已知数列的首项，．‎ ‎（1）求证：数列为等比数列；‎ ‎（2）记，若，求最大的正整数．‎ ‎17．（本题14分）一般地，对于直线及直线外一点，我们有点到直线的距离公式为：”‎ ‎（1）证明上述点到直线的距离公式；‎ ‎（2）设直线，试用上述公式求坐标原点到直线距离的最大值及取最大值时的值.‎ ‎18．（本题16分）如图所示，某街道居委会拟在EF地段的居民楼正南方向的空白地段AE上建一个活动中心，其中AE长为30米．活动中心东西走向，与居民楼平行．从东向西看活动中心的截面图的下部分是长方形ABCD，上部分是以DC为直径的半圆．为了保证居民楼住户的采光要求，活动中心在与半圆相切的太阳光线照射下落在居民楼上的影长GE不超过2.5米，其中该太阳光线与水平线的夹角θ满足tan θ＝.‎ ‎（1）若设计AB＝18米，AD＝6米，问能否保证上述采光要求？‎ ‎（2）在保证上述采光要求的前提下，如何设计AB与AD的长度，可使得活动中心的截面面积最大？‎ ‎(注：计算中π取3)‎ ‎19．（本题16分）在平面直角坐标系xOy中，直线x－y＋1＝0截以原点O为圆心的圆O所得的弦长为.‎ ‎（1）求圆O的方程；‎ ‎（2）若直线l与圆O相切于第一象限，且与坐标轴交于点D，E，当DE长最小时，求直线l的方程；‎ ‎（3）设M，P是圆O上任意两点，点M关于x轴的对称点为N，若直线MP，NP分别交x轴于点(m,0)和(n,0)，问mn是否为定值？若是，求出该定值；若不是，请说明理由．‎ ‎20．（本题16分）已知函数，，其中.‎ ‎（1）当时，求函数的值域；‎ ‎（2）当时，设，若给定，对于两个大于1的正数，存在满足：，，使恒成立，求实数的取值范围.‎ ‎（3）当时，设，若的最小值为，求实数的值.‎ ‎ ‎ 高二阶段性检测（一）‎ 数 学 试 卷 一、填空题：（本大题共14小题，每小题5分，共70分．）‎ ‎1．【答案】；‎ ‎2．【答案】 ；‎ ‎3．【答案】；‎ ‎4． 【答案】；‎ ‎5．【答案】9；‎ ‎6．【答案】9；‎ ‎7．【答案】；‎ ‎8． 【答案】‎ ‎9．【答案】‎ ‎10．【答案】25 ‎ ‎11．【答案】；‎ ‎12． 【答案】9； ‎ ‎13． 【答案】；‎ ‎14．【答案】‎ 二．本大题共6小题，共计90，请在答题卡指定区域内作答，解答时应写出文字说明、证明或演算步骤.‎ A M A1‎ C B B1‎ C1‎ N ‎15． ‎ ‎【答案】证明：（1）在中，‎ 在中，.‎ ‎，即为等腰三角形.‎ 又点为的中点，.‎ 又四边形为正方形,为的中点，‎ ‎,平面,平面 平面 ‎（2）证法一: 连接 由题意知,点分别为和的中点，. ‎ 又平面,平面, ‎ 平面. ‎ 证法二：取中点,连, ‎ 而分别为与的中点,‎ 平面,平面，‎ 平面, ‎ 同理可证平面 又 平面平面.‎ 平面， ‎ 平面.‎ ‎16． ‎ ‎【答案】（1）∵，∴，且∵，∴，‎ ‎ ∴数列为等比数列．‎ ‎（2）由（1）可求得，∴．‎ ‎ ， ‎ ‎ 若，则，∴．‎ ‎17．‎ ‎【答案】解：(1)证明：参照课本，但在课本过程的基础上要对或进行交待。‎ ‎ (2)由直线，由（1）中点到直线距离公式可得原点到直线距离为：‎ ‎，令，则，‎ ‎ 所以，‎ 当时，‎ 当时，‎ 若，则；‎ 若，‎ ‎ 综上可知：，且当，即时，可取最大值。‎ ‎18．‎ ‎【答案】解：如图，以A为坐标原点，AB所在直线为x轴，建立平面直角坐标系．‎ ‎（1）因为AB＝18米，AD＝6米，‎ 所以半圆的圆心为H(9,6)，半径r＝9.‎ 设太阳光线所在直线方程为y＝－x＋b，‎ 即3x＋4y－4b＝0，则由＝9，‎ 解得b＝24或b＝(舍)．‎ 故太阳光线所在直线方程为y＝－x＋24, ‎ 令x＝30，得EG＝1.5＜2.5.‎ 所以此时能保证上述采光要求．‎ ‎（2）设AD＝h米，AB＝2r米，‎ 则半圆的圆心为H(r，h)，半径为r.‎ 方法一　设太阳光线所在直线方程为y＝－x＋b，‎ 即3x＋4y－4b＝0，‎ 由＝r，解得b＝h＋2r或b＝h－(舍)．‎ 故太阳光线所在直线方程为y＝－x＋h＋2r，‎ 令x＝30，得EG＝2r＋h－，‎ 由EG≤，得h≤25－2r.‎ 所以S＝2rh＋πr2＝2rh＋×r2≤2r(25－2r)＋×r2‎ ‎＝－r2＋50r＝－(r－10)2＋250≤250.‎ 当且仅当r＝10时取等号．‎ 所以当AB＝20米且AD＝5米时，‎ 可使得活动中心的截面面积最大．‎ 方法二　欲使活动中心内部空间尽可能大，‎ 则影长EG恰为2.5米，则此时点G为(30,2.5)，‎ 设过点G的上述太阳光线为l1，‎ 则l1所在直线方程为y－＝－(x－30)，‎ 即3x＋4y－100＝0.‎ 由直线l1与半圆H相切，得r＝.‎ 而点H(r，h)在直线l1的下方，则3r＋4h－100＜0，‎ 即r＝－，从而h＝25－2r.‎ 又S＝2rh＋πr2＝2r(25－2r)＋×r2＝－r2＋50r＝－(r－10)2＋250≤250.当且仅当r＝10时取等号．‎ 所以当AB＝20米且AD＝5米时，‎ 可使得活动中心的截面面积最大．‎ ‎19． ‎ ‎【答案】解：（1）因为O到直线x－y＋1＝0的距离为，‎ 所以圆O的半径r＝ ＝，故圆O的方程为x2＋y2＝2.‎ ‎（2）设直线l的方程为＋＝1(a＞0，b＞0)，即bx＋ay－ab＝0，‎ 由直线l与圆O相切，得＝，即＋＝，‎ 所以DE2＝a2＋b2＝2(a2＋b2) ‎＝2≥2 ‎＝8(当且仅当a＝b＝2时等号成立)，‎ 此时直线l的方程为x＋y－2＝0.‎ ‎（3）设M(x1，y1)，P(x2，y2)，‎ 则N(x1，－y1)，x＋y＝2，x＋y＝2，‎ 直线MP与x轴的交点为，即m＝.‎ 直线NP与x轴的交点为，即n＝.‎ 所以mn＝·＝ ‎＝＝＝2，‎ 故mn＝2为定值．‎ ‎20．‎ ‎【答案】（1）;(2) ;(3) .‎ 解：（1）当时， ，因为，所以， ‎ 所以的值域为 ‎（2）由可得在区间上单调递增 　　‎ ‎①当时，有， ‎ ‎，得，同理，　　‎ ‎∴ 由的单调性知：、 从而有，符合题设. ‎ ‎②当时，， ， 由的单调性知 ， ∴，与题设不符 ③当时，同理可得， 得，与题设不符. ‎ ‎∴综合①、②、③得 ‎（3）因为当时， ，‎ 令， ，则，‎ 当时，即， ；‎ 当时， ，即，‎ 因为，所以， .‎ 若， ，此时，‎ 若，即，此时，所以实数.‎ ‎ ‎