高考数学专题复习课件：8-5直线、平面垂直的判定与性质

高考数学专题复习课件：8-5直线、平面垂直的判定与性质

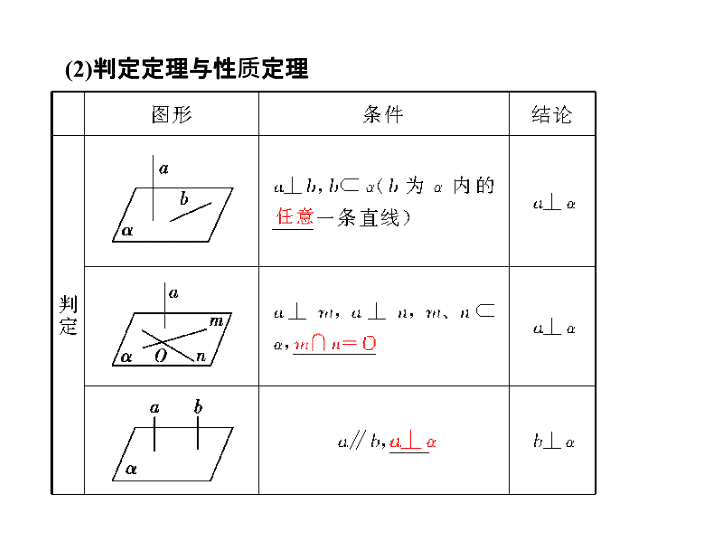
§8.5 　直线、平面垂直的判定与性质 [ 考纲要求 ] 　 1. 能以立体几何中的定义、公理和定理为出发点，认识和理解空间中线面垂直的有关性质和判定定理 .2. 能运用公理、定理和已获得的结论证明一些有关空间图形的位置关系的简单命题． 1 ． 直线与平面垂直 (1) 直线和平面垂直的定义 如果一条直线 l 与平面 α 内的 _______ 直线都垂直，就说直线 l 与平面 α 互相垂直． 任意 (2) 判定定理与性质定理 2. 平面与平面垂直 (1) 平面与平面垂直的定义 两个平面相交，如果它们所成的二面角是 __________ ，就说这两个平面互相垂直． 直二面角 (2) 判定定理与性质定理 【 思考辨析 】 　判断下面结论是否正确 ( 请在括号中打 “√” 或 “ ×” ) (1) 直线 l 与平面 α 内的无数条直线都垂直，则 l ⊥ α .( 　　 ) (2) 若直线 a ⊥ 平面 α ，直线 b ∥ α ，则直线 a 与 b 垂直． ( 　　 ) (3) 直线 a ⊥ α ， b ⊥ α ，则 a ∥ b .( 　　 ) (4) 若 α ⊥ β ， a ⊥ β ⇒ a ∥ α .( 　　 ) (5) a ⊥ α ， a ⊂ β ⇒ α ⊥ β .( 　　 ) (6) 若两平面垂直，则其中一个平面内的任意一条直线垂直于另一个平面． ( 　　 ) 【 答案 】 (1) × 　 (2) √ 　 (3) √ 　 (4) × 　 (5) √ 　 (6) × 1 ． ( 教材改编 ) 下列条件中，能判定直线 l ⊥ 平面 α 的是 ( 　　 ) A ． l 与平面 α 内的两条直线垂直 B ． l 与平面 α 内无数条直线垂直 C ． l 与平面 α 内的某一条直线垂直 D ． l 与平面 α 内任意一条直线垂直 【 解析 】 由直线与平面垂直的定义，可知 D 正确． 【 答案 】 D 2 ．设平面 α 与平面 β 相交于直线 m ，直线 a 在平面 α 内，直线 b 在平面 β 内，且 b ⊥ m ，则 “ α ⊥ β ” 是 “ a ⊥ b ” 的 ( 　　 ) A ．充分不必要条件 B ．必要不充分条件 C ．充分必要条件 D ．既不充分也不必要条件 【 解析 】 若 α ⊥ β ，因为 α ∩ β ＝ m ， b ⊂ β ， b ⊥ m ，所以根据两个平面垂直的性质定理可得 b ⊥ α ，又 a ⊂ α ，所以 a ⊥ b ；反过来，当 a ∥ m 时，因为 b ⊥ m ，且 a ， m 共面，一定有 b ⊥ a ，但不能保证 b ⊥ α ，所以不能推出 α ⊥ β . 【 答案 】 A 3 ． (2017· 上海六校联考 ) 已知 m 和 n 是两条不同的直线， α 和 β 是两个不重合的平面，下面给出的条件中一定能推出 m ⊥ β 的是 ( 　　 ) A ． α ⊥ β 且 m ⊂ α 　　　　 　 B ． α ⊥ β 且 m ∥ α C ． m ∥ n 且 n ⊥ β D ． m ⊥ n ， n ⊂ α 且 α ∥ β 【 解析 】 由线线平行性质的传递性和线面垂直的判定定理，可知 C 正确． 【 答案 】 C 4 ． ( 教材改编 ) PD 垂直于正方形 ABCD 所在的平面，连接 PB ， PC ， PA ， AC ， BD ，则一定互相垂直的平面有 ________ 对． 【 解析 】 由于 PD ⊥ 平面 ABCD ，故平面 PAD ⊥ 平面 ABCD ，平面 PDB ⊥ 平面 ABCD ，平面 PDC ⊥ 平面 ABCD ，平面 PDA ⊥ 平面 PDC ，平面 PAC ⊥ 平面 PDB ，平面 PAB ⊥ 平面 PAD ，平面 PBC ⊥ 平面 PDC ，共 7 对． 【 答案 】 7 5 ． ( 教材改编 ) 在三棱锥 P ABC 中，点 P 在平面 ABC 中的射影为点 O ， (1) 若 PA ＝ PB ＝ PC ，则点 O 是 △ ABC 的 ________ 心． (2) 若 PA ⊥ PB ， PB ⊥ PC ， PC ⊥ PA ，则点 O 是 △ ABC 的 ________ 心． 【 解析 】 (1) 如图 1 ，连接 OA ， OB ， OC ， OP ， 在 Rt △ POA 、 Rt △ POB 和 Rt △ POC 中， PA ＝ PC ＝ PB ，所以 OA ＝ OB ＝ OC ， 即 O 为 △ ABC 的外心． (2) 如图 2 ， ∵ PC ⊥ PA ， PB ⊥ PC ， PA ∩ PB ＝ P ， ∴ PC ⊥ 平面 PAB ， AB ⊂ 平面 PAB ， ∴ PC ⊥ AB ， 又 AB ⊥ PO ， PO ∩ PC ＝ P ， ∴ AB ⊥ 平面 PGC ， 又 CG ⊂ 平面 PGC ， ∴ AB ⊥ CG ，即 CG 为 △ ABC 边 AB 的高． 同理可证 BD ， AH 为 △ ABC 底边上的高， 即 O 为 △ ABC 的垂心． 【 答案 】 (1) 外　 (2) 垂 题型一　直线与平面垂直的判定与性质 【 例 1 】 (1) (2017· 武汉调研 ) 如图所示，在四棱锥 P ABCD 中，底面 ABCD 为矩形， PA ⊥ 平面 ABCD ，点 E 在线段 PC 上， PC ⊥ 平面 BDE . 证明： BD ⊥ 平面 PAC . 【 证明 】 ∵ PA ⊥ 平面 ABCD ， BD ⊂ 平面 ABCD ， ∴ PA ⊥ BD . ∵ PC ⊥ 平面 BDE ， BD ⊂ 平面 BDE ， ∴ PC ⊥ BD . 又 ∵ PA ∩ PC ＝ P ， ∴ BD ⊥ 平面 PAC . 所以 CD 2 ＋ DB 2 ＝ BC 2 ，即 CD ⊥ AO . 因为 PD ⊥ 平面 ABC ， CD ⊂ 平面 ABC ， 所以 PD ⊥ CD ，由 PD ∩ AO ＝ D 得， CD ⊥ 平面 PAB ， 又 PA ⊂ 平面 PAB ，所以 PA ⊥ CD . 【 方法规律 】 (1) 证明直线和平面垂直的常用方法： ① 判定定理； ② 垂直于平面的传递性 ( a ∥ b ， a ⊥ α ⇒ b ⊥ α ) ； ③ 面面平行的性质 ( a ⊥ α ， α ∥ β ⇒ a ⊥ β ) ； ④ 面面垂直的性质． (2) 证明线面垂直的核心是证线线垂直，而证明线线垂直则需借助线面垂直的性质．因此，判定定理与性质定理的合理转化是证明线面垂直的基本思想． (3) 线面垂直的性质，常用来证明线线垂直． 跟踪训练 1 (2017· 淄博模拟 ) 如图，在四棱锥 P ABCD 中，底面 ABCD 是矩形，侧棱 PD ⊥ 底面 ABCD ， PD ＝ DC ， E 是 PC 的中点，作 EF ⊥ PB 交 PB 于点 F . (1) 证明： PA ∥ 平面 EDB ； (2) 证明： PB ⊥ 平面 EFD . 【 证明 】 (1) 连接 AC 交 BD 于 O ，连接 EO . ∵ 底面 ABCD 是矩形， ∴ 点 O 是 AC 的中点． 又 ∵ E 是 PC 的中点， ∴ 在 △ PAC 中， EO 为中位线． ∴ PA ∥ EO ， 而 EO ⊂ 平面 EDB ， PA ⊄ 平面 EDB ， ∴ PA ∥ 平面 EDB . (2) 由 PD ⊥ 底面 ABCD ，得 PD ⊥ BC . ∵ 底面 ABCD 是矩形， ∴ DC ⊥ BC ，且 PD ∩ CD ＝ D ， ∴ BC ⊥ 平面 PDC ，而 DE ⊂ 平面 PDC ， ∴ BC ⊥ DE . ① ∵ PD ＝ DC ， E 是 PC 的中点， ∴△ PDC 是等腰三角形，故 DE ⊥ PC . ② 由 ① 和 ② 及 BC ∩ PC ＝ C ，得 DE ⊥ 平面 PBC ， 而 PB ⊂ 平面 PBC ， ∴ DE ⊥ PB . 又 EF ⊥ PB 且 DE ∩ EF ＝ E ， ∴ PB ⊥ 平面 EFD . 题型二　平面与平面垂直的判定与性质 【 例 2 】 (1) (2017· 济宁模拟 ) 如图 1 ，在四棱锥 P ABCD 中 ， PA ⊥ 底面 ABCD ，平面 ABCD 为正方形， E 为侧棱 PD 上一点， F 为 AB 上一点，该四棱锥的正 ( 主 ) 视图和侧 ( 左 ) 视图如图 2 所示． ① 求四面体 PBFC 的体积； ② 证明： AE ∥ 平面 PFC ； ③ 证明：平面 PFC ⊥ 平面 PCD . ③ 证明 ∵ PA ⊥ 平面 ABCD ， ∴ PA ⊥ CD . ∵ 平面 ABCD 为正方形， ∴ AD ⊥ CD . ∴ CD ⊥ 平面 PAD ， ∵ AE ⊂ 平面 PAD ， ∴ CD ⊥ AE . ∵ PA ＝ AD ， E 为 PD 中点， ∴ AE ⊥ PD . CD ∩ PD ＝ D ， ∴ AE ⊥ 平面 PCD . ∵ AE ∥ FQ ， ∴ FQ ⊥ 平面 PCD . ∵ PQ ⊂ 平面 PFC ， ∴ 平面 PFC ⊥ 平面 PCD . (2) (2017· 云南名校联考 ) 如图， AB 为圆 O 的直径，点 E ， F 在圆 O 上，且 AB ∥ EF ，矩形 ABCD 所在的平面和圆 O 所在的平面互相垂直，且 AD ＝ EF ＝ AF ＝ 1 ， AB ＝ 2. ① 求证：平面 AFC ⊥ 平面 CBF ； ② 在线段 CF 上是否存在一点 M ，使得 OM ∥ 平面 DAF ？并说明理由． 【 解析 】 ① 证明 ∵ 平面 ABCD ⊥ 平面 ABEF ， CB ⊥ AB ， 平面 ABCD ∩ 平面 ABEF ＝ AB ， ∴ CB ⊥ 平面 ABEF ， ∵ AF ⊂ 平面 ABEF ， ∴ AF ⊥ CB ， 又 ∵ AB 为圆 O 的直径， ∴ AF ⊥ BF ， ∵ CB ∩ BF ＝ B ， ∴ AF ⊥ 平面 CBF . ∵ AF ⊂ 平面 AFC ， ∴ 平面 AFC ⊥ 平面 CBF . ∴ MNAO 为平行四边形， ∴ OM ∥ AN ，又 AN ⊂ 平面 DAF ， OM ⊄ 平面 DAF ， ∴ OM ∥ 平面 DAF . 即存在一点 M 为 CF 的中点，使得 OM ∥ 平面 DAF . 【 方法规律 】 面面垂直的性质应用技巧 (1) 两平面垂直，在一个平面内垂直于交线的直线必垂直于另一个平面．这是把面面垂直转化为线面垂直的依据，运用时要注意 “ 平面内的直线 ” ． (2) 两个相交平面同时垂直于第三个平面，那么它们的交线也垂直于第三个平面，此性质在不是很复杂的题目中，要对此进行证明． 题型三　线面角、二面角的求法 【 例 3 】 如图，在四棱锥 P ABCD 中， PA ⊥ 底面 ABCD ， AB ⊥ AD ， AC ⊥ CD ， ∠ ABC ＝ 60 ° ， PA ＝ AB ＝ BC ， E 是 PC 的中点． (1) 求 PB 和平面 PAD 所成的角的大小； (2) 证明： AE ⊥ 平面 PCD ； (3) 求二面角 A PD C 的正弦值． 【 解析 】 (1) 在四棱锥 P ABCD 中， 因为 PA ⊥ 底面 ABCD ， AB ⊂ 平面 ABCD ， 故 PA ⊥ AB . 又 AB ⊥ AD ， PA ∩ AD ＝ A ， 从而 AB ⊥ 平面 PAD ， 故 PB 在平面 PAD 内的射影为 PA ， 从而 ∠ APB 为 PB 和平面 PAD 所成的角． 在 Rt △ PAB 中， AB ＝ PA ，故 ∠ APB ＝ 45 ° . 所以 PB 和平面 PAD 所成的角的大小为 45 ° . (2) 证明 在四棱锥 P ABCD 中， 因为 PA ⊥ 底面 ABCD ， CD ⊂ 平面 ABCD ， 故 CD ⊥ PA . 由条件 CD ⊥ AC ， PA ∩ AC ＝ A ， ∴ CD ⊥ 平面 PAC . 又 AE ⊂ 平面 PAC ， ∴ AE ⊥ CD . 由 PA ＝ AB ＝ BC ， ∠ ABC ＝ 60 ° ，可得 AC ＝ PA . ∵ E 是 PC 的中点， ∴ AE ⊥ PC . 又 PC ∩ CD ＝ C ，综上得 AE ⊥ 平面 PCD . (3) 过点 E 作 EM ⊥ PD ，垂足为 M ，连接 AM ，如图所示． 由 (2) 知， AE ⊥ 平面 PCD ， AM 在平面 PCD 内的射影是 EM ， 则可证得 AM ⊥ PD . 因此 ∠ AME 是二面角 A PD C 的平面角． 由已知，可得 ∠ CAD ＝ 30 ° . 设 AC ＝ a ，可得 【 方法规律 】 求线面角、二面角的常用方法： (1) 线面角的求法：找出斜线在平面上的射影，关键是作垂线，找垂足，要把线面角转化到一个三角形中求解． (2) 二面角的大小求法：二面角的大小用它的平面角来度量．平面角的作法常见的有 ① 定义法； ② 垂面法．注意利用等腰、等边三角形的性质． 跟踪训练 3 (2015· 山东 ) 如图，在三棱台 DEF ABC 中， AB ＝ 2 DE ， G ， H 分别为 AC ， BC 的中点． (1) 求证： BD ∥ 平面 FGH . (2) 若 CF ⊥ 平面 ABC ， AB ⊥ BC ， CF ＝ DE ， ∠ BAC ＝ 45 ° ，求平面 FGH 与平面 ACFD 所成的角 ( 锐角 ) 的大小． 【 解析 】 (1) 证明 方法一 如图，连接 DG ， CD ，设 CD ∩ GF ＝ O ，连接 OH ，在三棱台 DEF ABC 中， AB ＝ 2 DE ， G 为 AC 的中点， 可得 DF ∥ GC ， DF ＝ GC ，所以四边形 DFCG 为平行四边形． 则 O 为 CD 的中点，又 H 为 BC 的中点， 所以 OH ∥ BD ，又 OH ⊂ 平面 FGH ， BD ⊄ 平面 FGH ， 所以 BD ∥ 平面 FGH . 方法二 如图，在三棱台 DEF ABC 中，由 BC ＝ 2 EF ， H 为 BC 的中点， 可得 BH ∥ EF ， BH ＝ EF ， 所以四边形 BHFE 为平行四边形，可得 BE ∥ HF . 在 △ ABC 中， G 为 AC 的中点， H 为 BC 的中点， 所以 GH ∥ AB . 又 GH ∩ HF ＝ H ，所以平面 FGH ∥ 平面 ABED . 因为 BD ⊂ 平面 ABED ，所以 BD ∥ 平面 FGH . 方法二 如图，作 HM ⊥ AC 于点 M ，作 MN ⊥ GF 于点 N ， 连接 NH . 设 AB ＝ 2 ，则 CF ＝ 1. 由 FC ⊥ 平面 ABC ，得 HM ⊥ FC ， 又 FC ∩ AC ＝ C ，所以 HM ⊥ 平面 ACFD . 因此 GF ⊥ NH ，所以 ∠ MNH 即为所求的角． 思想与方法系列 16 立体几何证明问题中的转化思想 【 典例 】 (12 分 ) 如图所示， M ， N ， K 分别是正方体 ABCD A 1 B 1 C 1 D 1 的棱 AB ， CD ， C 1 D 1 的中点． 求证： (1) AN ∥ 平面 A 1 MK ； (2) 平面 A 1 B 1 C ⊥ 平面 A 1 MK . 【 思维点拨 】 (1) 要证线面平行，需证线线平行． (2) 要证面面垂直，需证线面垂直，要证线面垂直，需证线线垂直． 【 规范解答 】 证明 (1) 如图所示，连接 NK . 在正方体 ABCD A 1 B 1 C 1 D 1 中， ∵ 四边形 AA 1 D 1 D ， DD 1 C 1 C 都为正方形， ∴ AA 1 ∥ DD 1 ， AA 1 ＝ DD 1 ， C 1 D 1 ∥ CD ， C 1 D 1 ＝ CD .(2 分 ) ∵ N ， K 分别为 CD ， C 1 D 1 的中点， ∴ DN ∥ D 1 K ， DN ＝ D 1 K ， ∴ 四边形 DD 1 KN 为平行四边形． (3 分 ) ∴ KN ∥ DD 1 ， KN ＝ DD 1 ， ∴ AA 1 ∥ KN ， AA 1 ＝ KN . ∴ 四边形 AA 1 KN 为平行四边形． ∴ AN ∥ A 1 K .(4 分 ) ∵ A 1 K ⊂ 平面 A 1 MK ， AN ⊄ 平面 A 1 MK ， ∴ AN ∥ 平面 A 1 MK .(6 分 ) (2) 如上图所示，连接 BC 1 . 在正方体 ABCD A 1 B 1 C 1 D 1 中， AB ∥ C 1 D 1 ， AB ＝ C 1 D 1 . ∵ M ， K 分别为 AB ， C 1 D 1 的中点， ∴ BM ∥ C 1 K ， BM ＝ C 1 K . ∴ 四边形 BC 1 KM 为平行四边形． ∴ MK ∥ BC 1 .(8 分 ) 在正方体 ABCD A 1 B 1 C 1 D 1 中， A 1 B 1 ⊥ 平面 BB 1 C 1 C ， BC 1 ⊂ 平面 BB 1 C 1 C ， ∴ A 1 B 1 ⊥ BC 1 . ∵ MK ∥ BC 1 ， ∴ A 1 B 1 ⊥ MK . ∵ 四边形 BB 1 C 1 C 为正方形， ∴ BC 1 ⊥ B 1 C .(10 分 ) ∴ MK ⊥ B 1 C . ∵ A 1 B 1 ⊂ 平面 A 1 B 1 C ， B 1 C ⊂ 平面 A 1 B 1 C ， A 1 B 1 ∩ B 1 C ＝ B 1 ， ∴ MK ⊥ 平面 A 1 B 1 C . 又 ∵ MK ⊂ 平面 A 1 MK ， ∴ 平面 A 1 B 1 C ⊥ 平面 A 1 MK .(12 分 ) 【 温馨提醒 】 (1) 线面平行、垂直关系的证明问题的指导思想是线线、线面、面面关系的相互转化，交替使用平行、垂直的判定定理和性质定理． (2) 线线关系是线面关系、面面关系的基础．证明过程中要注意利用平面几何中的结论，如证明平行时常用的中位线、平行线分线段成比例；证明垂直时常用的等腰三角形的中线等． (3) 证明过程一定要严谨，使用定理时要对照条件、步骤书写要规范 . ► 方法与技巧 1 ．三类论证 (1) 证明线线垂直的方法 ① 定义：两条直线所成的角为 90 ° ； ② 平面几何中证明线线垂直的方法； ③ 线面垂直的性质： a ⊥ α ， b ⊂ α ⇒ a ⊥ b ； ④ 线面垂直的性质： a ⊥ α ， b ∥ α ⇒ a ⊥ b . (3) 证明面面垂直的方法 ① 利用定义：两个平面相交，所成的二面角是直二面角； ② 判定定理： a ⊂ α ， a ⊥ β ⇒ α ⊥ β . 在证明两平面垂直时一般先从现有的直线中寻找平面的垂线，若这样的直线图中不存在，则可通过作辅助线来解决． ► 失误与防范 1 ．在解决直线与平面垂直的问题过程中，要注意直线与平面垂直的定义、判定定理和性质定理的联合交替使用，即注意线线垂直和线面垂直的互相转化． 2 ．面面垂直的性质定理是作辅助线的一个重要依据．我们要作一个平面的一条垂线，通常是先找这个平面的一个垂面，在这个垂面中，作交线的垂线即可 .