2018届二轮复习立体几何理学案（全国通用）

2018届二轮复习立体几何理学案（全国通用）

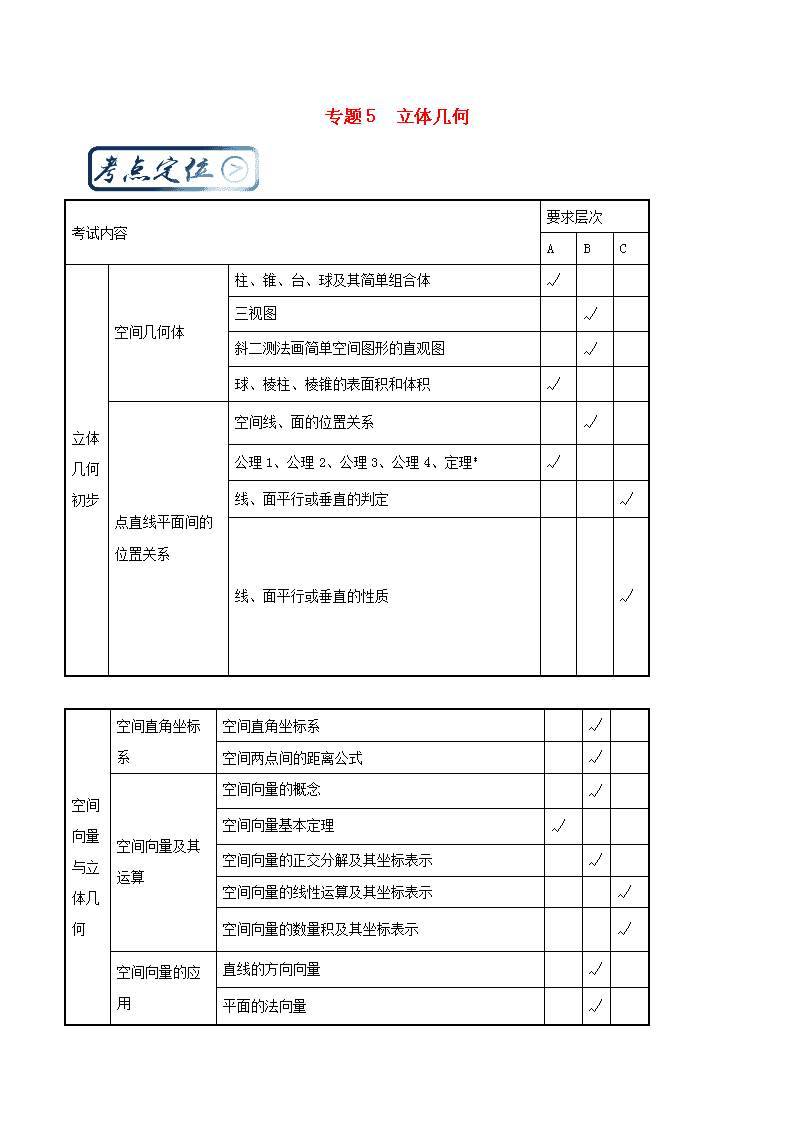
专题5 立体几何 考试内容 要求层次 A B C 立体几何初步 空间几何体 柱、锥、台、球及其简单组合体 ‎√‎ 三视图 ‎√‎ 斜二测法画简单空间图形的直观图 ‎√‎ 球、棱柱、棱锥的表面积和体积 ‎√‎ 点直线平面间的位置关系 空间线、面的位置关系 ‎√‎ 公理1、公理2、公理3、公理4、定理*‎ ‎√‎ 线、面平行或垂直的判定 ‎√‎ 线、面平行或垂直的性质 ‎√‎ 空间 向量 与立 体几 何 空间直角坐标系 空间直角坐标系 ‎√‎ 空间两点间的距离公式 ‎√‎ 空间向量及其运算 空间向量的概念 ‎√‎ 空间向量基本定理 ‎√‎ 空间向量的正交分解及其坐标表示 ‎√‎ 空间向量的线性运算及其坐标表示 ‎√‎ 空间向量的数量积及其坐标表示 ‎√‎ 空间向量的应用 直线的方向向量 ‎√‎ 平面的法向量 ‎√‎ 线、面位置关系 ‎√‎ 线线、线面、面面的夹角 ‎√‎ 说明: A.了解 B.理解 C.掌握 立体几何是高考必考重点内容之一，理科高考解答题考查特点为；一般分2个小问题，考题往往以多面体为依托，第（1）小问考查线线、线面、面面的位置关系，第（2）问考查面空间角的计算。 学习中即要培养学生的逻辑推理能力，也要训练运用空间向量的运算解决解几何问题。训练学生的直观想象能力及运算能力。‎ 复习教学中提出以下建议；教学中应注意“四化”，知识理解“深化”、考试题型“类化”、通性通法“强化”、解题思维“优化”。高考复习内容四查：查考纲把握方向、查考题明辨重点、查课本回归基础、查学情对症下药。数学教学与高考复习要求四通：对学生点，心有灵犀一点通；让学生悟，融会贯通；让学生做，触类旁通；让学生考，无师自通。‎ ‎★★★‎ 通过研究近4年全国高考试卷，高考中立体几何试题主要以中档题出现，通过研究近几年全国高考试卷，题目设置上，会有1--2个选填题；分值为5--10分。解答题1道为12分。‎ ‎○○○○‎ 立体几何部分在高考中占据重要的地位，通过分析近几年的高考情况，解答题考查特点如下表：‎ 考什么 怎么考 难度 ‎1.平行与垂直 ‎①考查直线与直线；‎ ‎②考查直线和平面；‎ ‎③考查平面与平面；‎ 中档题 ‎2. 空间向量与 空间角的求解 ‎①求异面直线所成的角；‎ ‎②求线面角的正弦 ‎③求二面角的余弦 ‎ 中档题 ‎ 2014-2017年全国高考立体几何（理科）试题分布表 年份 题型 考查角度 分值 难度 ‎2017年Ⅰ卷 解答题第18题 ‎（1）面面垂直 （2）求二面角的余弦 ‎12‎ 中等 ‎2017年Ⅱ卷 解答题第19题 ‎（1）线面平行 （2）求二面角的余弦 ‎12‎ 中等 ‎2017年Ⅲ卷 解答题第19题 ‎（1）面面垂直 （2）求二面角的余弦 ‎12‎ 中等 ‎2016年Ⅰ卷 解答题第18题 ‎（1）面面垂直 （2）求二面角的余弦 ‎12‎ 中等 ‎2016年Ⅱ卷 解答题第19题 ‎（1）线面垂直 （2）求二面角的余弦 ‎12‎ 中等 ‎2016年Ⅲ卷 解答题第19题 ‎（1）线面平行 （2）求线面角的正弦 ‎12‎ 中等 ‎2015年Ⅰ卷 解答题第18题 ‎（1）面面垂直 （2）求异面直线所成的角 ‎12‎ 中等 ‎2015年Ⅱ卷 解答题第19题 ‎（1）画出平行线 （2）求线面角的正弦 ‎12‎ 中等 ‎2014年Ⅰ卷 解答题第19题 ‎（1）线段相等 （2）求二面角的余弦 ‎12‎ 中等 ‎2014年Ⅱ卷 解答题第19题 ‎（1）线面平行 （2）三棱锥的体积 ‎12‎ 中等 ‎1．平面的基本性质 名称 图形 文字语言 符号语言 公理1‎ 如果一条直线上的两点在一个平面内，那么这条直线在这个平面内 A∈l，B∈l，A∈α，B∈α⇒l⊂α 公理2‎ 过不在同一条直线上的三点，有且只有一个平面 A，B，C不共线⇒A，B，C∈平面α，则α是唯一的 公理2的推论 推论1‎ 经过一条直线和直线外的一点，有且只有一个平面 若点A∉直线a，则A和a确定一个平面α 推论2‎ 经过两条相交直线，有且只有一个平面 a∩b＝P⇒有且只有一个平面α，使a⊂α，b⊂α 推论3‎ 经过两条平行直线，有且只有一个平面 a∥b⇒有且只有一个平面α，使a⊂α，b⊂α 公理3‎ 如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线 若P∈α，P∈β，则α∩β＝a，P∈a，且a是唯一的 公理4‎ 平行于同一直线的两条直线平行 l1∥l，l2∥l⇒l1∥l2‎ ‎2．空间中点、线、面之间的位置关系 直线与直线 直线与平面 平面与平面 平行关系 相交关系 独有关系 ‎3．直线与平面平行的判定定理与性质定理 文字语言 图形语言 符号语言 判定定理 不在平面内的一条直线与此平面内的一条直线平行，则该直线与此平面平行(简记为线线平行⇒线面平行)‎ ⇒l∥α 性质定理 一条直线与一个平面平行，则过这条直线的任一平面与此平面的交线与该直线平行(简记为线面平行⇒线线平行)‎ ⇒a∥b ‎4．平面与平面平行的判定定理与性质定理 文字语言 图形语言 符号语言 ⇒α∥β 判定定理 一个平面内的两条相交直线与另一个平面平行，则这两个平面平行(简记为线面平行⇒面面平行)‎ 性质定理 如果两个平行平面同时和第三个平面相交，那么它们的交线平行 ⇒a∥b ‎5．直线与平面垂直的判定定理及性质定理 文字语言 图形语言 符号语言 判定定理 一条直线与平面内的两条相交直线都垂直，则该直线与此平面垂直 ⇒l⊥α 性质定理 垂直于同一个平面的两条直线平行 ⇒a∥b ‎6.平面与平面垂直的判定定理及性质定理 文字语言 图形语言 符号语言 判定定理 一个平面过另一个平面的一条垂线，则这两个平面互相垂直 ⇒α⊥β 性质定理 两个平面互相垂直，则一个平面内垂直于交线的直线垂直于另一个平面 ⇒l⊥α ‎7.空间向量在立体几何中的应用 ‎（1）直线的方向向量与平面的法向量的确定 ‎①直线的方向向量：l是空间一直线，A，B是直线l上任意两点，则称为直线l的方向向量，‎ 与平行的任意非零向量也是直线l的方向向量．‎ ‎②平面的法向量可利用方程组求出：设a，b是平面α内两不共线向量，n为平面α的法向量，‎ 则求法向量的方程组为.‎ ‎（2）两条异面直线所成的角；‎ ‎①定义：设a，b是两条异面直线，过空间任一点O作直线a′∥a，b′∥b，则a′与b′所夹的锐角或直角叫做a与b所成的角．‎ ‎②范围：两异面直线所成角θ的取值范围是．‎ ‎③向量求法：设直线a，b的方向向量为，其夹角为φ，则有.‎ ‎（3）直线和平面所成角的求法：如图所示，设直线l的方向向量为e，平面α的法向量为n，直线l与 平面α所成的角为φ，两向量e与n的夹角为θ，则有sin φ＝|cos θ|＝.‎ ‎（4）求二面角的大小 ‎①如图1，AB、CD是二面角α－l－β的两个面内与棱l垂直的直线，则二面角的大小θ＝〈，〉．‎ ‎②如图2、3，分别是二面角α－l－β的两个半平面α，β的法向量，则二面角的大小；‎ ‎(或)．‎ ‎（5）点面距的求法；如图，设AB为平面α的一条斜线段，为平面α的法向量，‎ 则B到平面α的距离.‎ 典例. 【2017课标II理19】如图，四棱锥P-ABCD中，侧面PAD为等比三角形且垂直于底面ABCD， E是PD的中点。‎ ‎（1）证明：直线 平面PAB；‎ ‎（2）点M在棱PC 上，且直线BM与底面ABCD所成角为 ，求二面角的余弦值。‎ ‎【答案】(1)证明略； (2) 。‎ ‎ ‎ 则，，，，,，‎ 设则，‎ 因为BM与底面ABCD所成的角为45°，而是底面ABCD的法向量，‎ 所以， ，‎ 即。 ①‎ 又M在棱PC上，设,则 ；。 ②‎ 由①，②解得 (舍去)，。‎ 所以，从而。‎ 设是平面ABM的法向量，则；即 所以可取。于是 ，‎ 因此二面角的余弦值为。‎ ‎【精准解读】本道立体几何解答题，分别考察了线与面平行的证明与二面角的计算。即考察了逻辑推理能力，也体现了对计算能力的考察。有一定的综合度。 对于(1)问中线面平行的证明，基本思路为：‎ 体现了空间问题向平面问题转化的思想；而（2）问中二面角的求解，其基本程序为；‎ 第一步：建系.建立空间直角坐标系：‎ ‎1.若图中有三条相互垂直的直线交于一点时，可直接利用这三条直线建系.‎ ‎2.若没有明显的三条互相垂直的直线，可以利用面面垂直的性质等作出互相垂直且交于一点的三条直线，建系.‎ 第二步：求出相关点、线段的坐标，求出相关面的法向量.‎ 第三步：利用数量积公式求角。体现了方程思想和求解的程序化思想。‎ ‎1.【2017课标3理19】如图，四面体ABCD中，△ABC是正三角形，△ACD是直角三角形，‎ ‎∠ABD=∠CBD，AB=BD．‎ ‎（1）证明：平面ACD⊥平面ABC；‎ ‎（2）过AC的平面交BD于点E，若平面AEC把四面体ABCD分成体积相等的两部分，‎ 求二面角D–AE–C的余弦值.‎ ‎【答案】(1)证明略； (2) .‎ ‎【解析】（1）由题设可得，，从而 ‎ 又是直角三角形，所以，‎ 取AC的中点O，连接DO,BO,则DO⊥AC,DO=AO 又由于△ABC是正三角形，故.所以为二面角 的平面角.‎ 在Rt△AOB中， .‎ 又 ，所以 ，‎ 故 ，所以平面ACD⊥平面ABC.‎ ‎（2）‎ 由题设及（1）知，两两垂直，以为坐标原点，的方向为轴正方向，‎ 为单位长，建立如图所示的空间直角坐标系.‎ 则 ‎ 由题设知，四面体ABCE的体积为四面体ABCD的体积的，‎ 从而E到平面ABC的距离为D到平面ABC的距离的，即E为DB的中点，得 .‎ 故 .‎ 设是平面DAE的法向量，则即 ‎ 可取 .设是平面AEC的法向量，‎ 则同理可得 .‎ 则 .所以二面角D-AE-C的余弦值为 .‎ ‎【精准解读】本题考查了平面与平面垂直的证明，基本思路为；证面面垂直，运用面与面垂直的判定定理可转化为证明线与面垂直，再转化为线与线垂直。而证明途径的寻找则需要空间观察能力，依靠平时的经验积累与分析思维的能力。二面角的求解可依靠空间向量解决。‎ ‎2.【2017西安模拟】如图，在梯形中，，，，四边形为矩形，平面平面，．‎ ‎（1）求证：平面；‎ ‎（2）点在线段上运动，设平面与平面所成二面角的平面角为，‎ 试求的取值范围．‎ ‎【答案】（1）详见解析；（2）．‎ ‎（2）由（1）可建立分别以直线，，为轴，轴，轴，‎ 如图所示空间直角坐标系，‎ 令，则，，‎ ‎，，∴，，‎ 设为平面的一个法向量，‎ 由得，取，则，‎ ‎∵是平面的一个法向量，‎ ‎∴，‎ ‎∵，∴当时，有最小值，‎ 当时，有最大值，∴．‎ ‎【精准解读】本题考查了线与平面垂直的证明，基本思路为有2条；1是运用线与面垂直的判定定理转化证为线与线垂直。2是可运用面与面垂直的性质证明。（2）问中二面角范围的求解可依靠空间向量再结合二次函数来解决。‎ ‎3.【2017衡水金卷】如图，在矩形中，已知，点、分别在、上，且，将四边形沿折起，使点在平面上的射影在直线上．‎ ‎（I）求证：；‎ ‎（II）求点到平面的距离；‎ ‎（III）求直线与平面所成的正弦值．‎ ‎【答案】（1）见解析（2）2（3）‎ ‎（2）延长交于点，因为 点到平面的距离为点到平面距离的，‎ 点平面的距离为，而，‎ 直线与平面新角的正弦值为．‎ 法二：（2）如图，过点作，过点作平面，分别以、、‎ 为、、轴建立空间直角坐标系，‎ 设点，由于，‎ 解得于是，所以线段的长度为．‎ 即点到平面的距离为．‎ ‎（3）从而，故，‎ 设平面的一个法向量为，设直线与平面所成角的大小为，‎ 则 ‎【精准解读】（1）问考查了线与线垂直的证明，基本思路为转化为线与线所在的平面垂直。（2）问考查了点到面的距离。方法有2，其一是运用等体积法解决，其二可运用空间向量求解。（3）问求解线面角可依靠空间向量来解决。‎ ‎【实战演练】（共100分）‎ 一、选择题（共4题，每题5分）‎ ‎1.【2017长春模拟】给出下列关于互不相同的直线、、和平面、的四个命题：‎ ‎①若，，点，则与不共面；‎ ‎②若、是异面直线，，，且，，则；‎ ‎③若，，，则；‎ ‎④若，，，，，则，‎ 其中为真命题的是( )‎ A．①③④ B．②③④ C．①②④ D．①②③‎ ‎【答案】C ‎【解析】①符合异面直线判定定理，①正确；由、是异面直线，，得存在两条相交直线、，满足，，由于，，所以，，即，②正确；③满足条件，，的直线、位置关系不定，可以平行，相交或异面，③不正确；④符号面面平行判定定理，故正确，选C.‎ ‎2.【2017课标II理10】已知直三棱柱中，，，，则异面直线与所成角的余弦值为（ ）‎ A． B． C． D．‎ ‎【答案】C ‎ ‎ ‎3.【2017浙江高考9】如图，已知正四面体D–ABC（所有棱长均相等的三棱锥），P，Q，R分别为AB，BC，CA上的点，AP=PB，，分别记二面角D–PR–Q，D–PQ–R，D–QR–P的平面角为α，β，γ，则（ ）‎ A．γ<α<β B．α<γ<β C．α<β<γ D．β<γ<α ‎【答案】B ‎【解析】设O为三角形ABC中心，则O到PQ距离最小，O到PR距离最大，O到RQ距离居中，而高相等，因此，所以选B．‎ ‎4.【2017江西二模】三棱柱ABC﹣A1B‎1C1的侧棱与底面垂直，AA1=AB=AC=1，AB⊥AC，N是BC的中点，点P在A1B1上，且满足=λ，直线PN与平面ABC所成角θ的正切值取最大值时λ的值为（　　）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】以AB、AC、AA1分别为x轴、y轴、z轴，建立空间直角坐标系A﹣xyz，‎ 则=（﹣λ，），易得平面ABC的一个法向量为=（0，0，1）‎ 则直线PN与平面ABC所成的角θ满足：sinθ=|cos＜，＞|=，‎ 于是问题转化为二次函数求最值，而θ∈[0，]，‎ 当θ最大时，sinθ最大，所以当λ=时，sinθ最大为，‎ 同时直线PN与平面ABC所成的角θ得到最大值．选：A．‎ 二、填空题（共4题，每题5分）‎ ‎5.【2017银川模拟】如图所示，正方体ABCD﹣A′B′C′D′的棱长为1，E、F分别是棱AA′，CC′的中点，过直线EF的平面分别与棱BB′，DD′交于M，N，给出以下四个命题：‎ ‎①平面MENF一定为矩形；‎ ‎②平面MENF⊥平面BDD′B′；‎ ‎③当M为BB1的中点时，MENF的面积最小；‎ ‎④四棱锥A﹣MENF的体积为常数． 以上命题中正确命题的序号为　 　．‎ ‎【答案】：②③④‎ ‎ ‎ ‎6.【2017福建莆田一模】如图，在菱形ABCD中，M为AC与BD的交点，∠BAD=，AB=3，将△CBD沿BD折起到△C1BD的位置，若点A，B，D，C1都在球O的球面上，且球O的表面积为16π，则直线C‎1M与平面ABD所成角的正弦值为　 　．‎ ‎【答案】‎ ‎【解析】如图所示，‎ 设O为球心，E、F分别为△ABD、△C1BD的外接圆圆心，‎ 则有OE⊥面ABD，OF⊥面C1BD，∵菱形ABCD中，∠BAD=，AB=3‎ ‎∴△ABD、△C1BD为等边△，故E、F分别为△ABD、△C1BD的中心．‎ ‎∵球O的表面积为16π，∴球半径为2．‎ 在直角△AOM中，OA=2，AE=，⇒QE=1．tan∠OME=，‎ ‎∵C‎1M⊥DB，AM⊥DB，∴DB⊥面AMC1，‎ ‎∴∠C1MA（或其补角）就是直线C‎1M与平面ABD所成角．‎ ‎∠C1MA=2∠OME，tan∠C1MA=tan（2∠OME）=，sin∠C1MA=，‎ 直线C‎1M与平面ABD所成角的正弦值为，故答案为：．‎ ‎7.【2017南昌模拟】在底面是菱形的四棱锥P﹣ABCD中，PA⊥底面ABCD，∠BAD=120°，点E为棱PB的中点，点F在棱AD上，平面CEF与PA交于点K，且PA=AB=3，AF=2，则点K到平面PBD的距离为　　．‎ ‎【答案】‎ ‎【解析】如图所示，以AP为z轴，AD为y轴，取BC的中点M，以AM为x轴，建立空间直角坐标系．则A（0，0，0），P（0，0，3），D（0，3，0），F（0，2，0），‎ B（，﹣，0），C（，，0），E（，﹣，），‎ 设K（0，0，m），则=+b，∴（0，0，m）=，‎ ‎∴a﹣b=0，=0，a=m，解得m=，a=，b=．‎ ‎=，=（0，3，﹣3）．‎ 设平面PBD的法向量为=（x，y，z），则，，‎ 取=（，1，1）．=．∴点K到平面PBD的距离d===．‎ ‎8.【2017兰州模拟】在正方体中，是棱的中点，是侧面内的动点，且平面，则与平面所成角的正切值的取值范围是 ．‎ ‎【答案】‎ ‎【解析】建立如所示的坐标系,则,‎ 设,平面的法向量为,则,所以,即,令,则,所以.‎ 又因为平面,所以,即,也即,‎ 所以.由于是平面的一个法向量,且,‎ 所以,记与平面所成角为,‎ 则,所以,‎ 因为,所以.‎ 三、解答题（共6题，每题10分）‎ ‎ 9.【2017课标1理18】如图，在四棱锥P-ABCD中，AB//CD，且.‎ ‎（1）证明：平面PAB⊥平面PAD；‎ ‎（2）若PA=PD=AB=DC，，求二面角A-PB-C的余弦值.‎ ‎【答案】见解析 ‎【解析】（1）由已知，得AB⊥AP，CD⊥PD.‎ 由于AB∥CD ，故AB⊥PD ，从而AB⊥平面PAD.‎ 又AB 平面PAB，所以平面PAB⊥平面PAD.‎ ‎（2）在平面内作，垂足为，‎ 由（1）可知，平面，故，可得平面.‎ 以为坐标原点，的方向为轴正方向，为单位长，建立如图所示的空间直角坐标系.‎ 由（1）及已知可得，，，.‎ 所以，，，.‎ 设是平面的法向量，则，即，‎ 可取.设是平面的法向量，则，即，‎ 可取.则，所以二面角的余弦值为.‎ ‎10.【2017山东理17】如图，几何体是圆柱的一部分，它是由矩形（及其内部）以边所在直线为旋转轴旋转得到的，是的中点.‎ ‎（Ⅰ）设是上的一点，且，求的大小；‎ ‎（Ⅱ）当，，求二面角的大小.‎ ‎【答案】（Ⅰ）.（Ⅱ）.‎ ‎【解析】（Ⅰ）因为，，，平面，，‎ 所以平面，又平面，‎ 所以，又，因此 ‎（Ⅱ）解法一：‎ 取的中点，连接，，. 因为，所以四边形为菱形，‎ 所以.‎ 取中点，连接，，.则，，‎ 所以为所求二面角的平面角.又，所以.‎ 在中，由于，由余弦定理得，‎ 所以，因此为等边三角形，故所求的角为.‎ 解法二：‎ 设是平面的一个法向量.由可得 取，可得平面的一个法向量.‎ 所以.因此所求的角为.‎ ‎11.【2017天津理17】如图，在三棱锥P-ABC中，PA⊥底面ABC，.点D，E，N分别为棱PA，PC，BC的中点， M是线段AD的中点，PA=AC=4，AB=2. ‎ ‎（Ⅰ）求证：MN∥平面BDE；‎ ‎（Ⅱ）求二面角C-EM-N的正弦值；‎ ‎（Ⅲ）已知点H在棱PA上，且直线NH与直线BE所成角的余弦值为，求线段AH的长.‎ ‎【答案】 （1）证明见解析（2） （3） 或 ‎ ‎【解析】（1）如图，以A为原点，分别以，，方向为x轴、y轴、z轴正方向建立空间直角坐标系.依题意可得A（0，0，0），B（2，0，0），C（0， 4，0），P（0，0，4），D（0，0，2），E（0，2，2），M（0，0，1），N（1，2，0）.‎ ‎（Ⅰ）证明：=（0，2，0），=（2，0，）.设，为平面BDE的法向量，‎ 则，即.不妨设，可得.又=（1，2，），‎ 可得.因为平面BDE，所以MN//平面BDE.‎ ‎（Ⅱ）易知为平面CEM的一个法向量.设为平面EMN的法向量，则，因为，，所以.不妨设，可得.‎ 因此有，于是.‎ 所以，二面角C—EM—N的正弦值为.‎ ‎ ‎ ‎12. 【2017海口模拟】如图，四棱锥的底面是正方形，侧棱⊥底面，，是的中点． ‎ ‎（Ⅰ）证明：//平面； ‎ ‎ （Ⅱ）求二面角的平面角的余弦值；‎ ‎ （Ⅲ）在棱上是否存在点，使⊥平面？证明你的结论． ‎ ‎【答案】（I）见解析 （II） （Ⅲ）见解析 ‎【解析】法一：（I）以D为坐标原点，分别以DA、DC、DP所在直线为x轴、y轴、z轴建立 空间直角坐标系，设PD=DC=2，则A(2,0,0),P(0,0,2),E(0,1,1),B(2,2,0)，‎ 设是平面BDE的一个法向量，则由 ，得取y=-1，‎ 得． ∵，‎ ‎∴，又PA平面BDE,∴PA∥平面BDE ‎（II）由（Ⅰ）知是平面BDE的一个法向量，‎ 又是平面DEC的一个法向量． ‎ 设二面角B-DE-C的平面角为，由图可知 ‎∴，故二面角B-DE-C的余弦值为． ‎ ‎（Ⅲ）∵，∴‎ 假设棱PB上存在点F，使PB⊥平面DEF，‎ 设，则，，‎ 由得，∴,此时，‎ 即在棱PB上存在点F，，使得PB⊥平面DEF．‎ 法二：（I）连接AC，AC交BD于O，连接OE．在中，OE为中位线，‎ ‎，又PA平面BDE,//平面BDE．‎ ‎（II）PD⊥底面ABCD,∴ 平面PDC⊥底面ABCD，CD为交线,∵BC⊥CD ‎∴面BCE⊥平面PDC，PC为交线, ∵PD=DC，E是PC的中点∴DE⊥PC ‎∴DE⊥平面PBC，∴DE⊥BE，∴即为二面角B-DE-C的平面角．‎ 设PD=DC=a，在中,‎ 故二面角B-DE-C的余弦值为．‎ ‎（Ⅲ）由（II）可知DE⊥平面PBC，所以DE⊥PB，‎ 所以在平面PDE内过D作DF⊥PB，连EF，则PB⊥平面DEF． ‎ 在中,PD=a,BD=．‎ 所以在棱PB上存在点F，，使得PB⊥平面DEF ．‎ ‎13. 【2017福州模拟】在四棱锥中，底面为平行四边形，，，，点在底面内的射影在线段上，且，，为的中点，在线段上，且．‎ ‎（Ⅰ）当时，证明：平面平面；‎ ‎（Ⅱ）当平面与平面所成的二面角的正弦值为时，求四棱锥的体积．‎ ‎【答案】（Ⅰ）见解析;（Ⅱ）.‎ ‎（Ⅱ）以为坐标原点，，，所在直线分别为轴，轴，轴建立如图所示的空间 直角坐标系，则，，，，，‎ ‎.平面的一个法向量为.‎ 设平面的法向量为，‎ 由，，得令，得.‎ 由题意可得，，解得，‎ 所以四棱锥的体积.‎ ‎14. 【2017哈尔滨模拟】如图，三棱柱中，，，分别为棱的中点.‎ ‎（1）在平面内过点作平面交于点，并写出作图步骤，但不要求证明.‎ ‎（2）若侧面侧面，求直线与平面所成角的正弦值.‎ ‎【答案】（1）见解析（2）‎ ‎【解析】（1）如图，在平面内，过点作交于点，连结，在中，作交于点，连结并延长交于点，则为所求作直线.‎ ‎（2）连结，∵，∴为正三角形.‎ ‎∵为的中点，∴，‎ 又∵侧面侧面，且面面，‎ 平面，∴平面，‎ 在平面内过点作交于点，‎ 分别以的方向为轴，轴，轴的正方向，建立如图所示的空间直角坐标系，则，.‎ 设直线与平面所成角为，‎ 则，‎ 即直线与平面所成角的正弦值为.‎ ‎________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________‎