2018届二轮复习 不等式与线性规划学案(全国通用)
第19讲 不等式与线性规划
(对应 生用书第113页)
一、选择题
1.(2017·山西吕梁二模)已知0
0 B.2a-b<
C.log2 a+log2 b<-2 D.2<
C [对于A,由log2 a>0得log2 a>log2 1,即a>1,而由01>b,矛盾,故B不正确.
对于C,当a、b>0时,log2 a+log2 b<-2⇔log2(ab)2可得ab<,故C正确.
对于D,由2<得+<,而由02,矛盾,故D不正确.
故选C.]
2.(2017·湖北四校联考)若变量x,y满足约束条件,则z=(x-1)2+y2的最大值为( )
【导 号:07804125】
A.4 B.
C.17 D.16
C [z=(x-1)2+y2表示点(x,y)与点P(1,0)间距离的平方.画出约束条件所表示的平面区域如图中阴影部分所示,易知P(1,0)与A(2,4)间的距离最大,因此zmax=(2-1)2+42=17.]
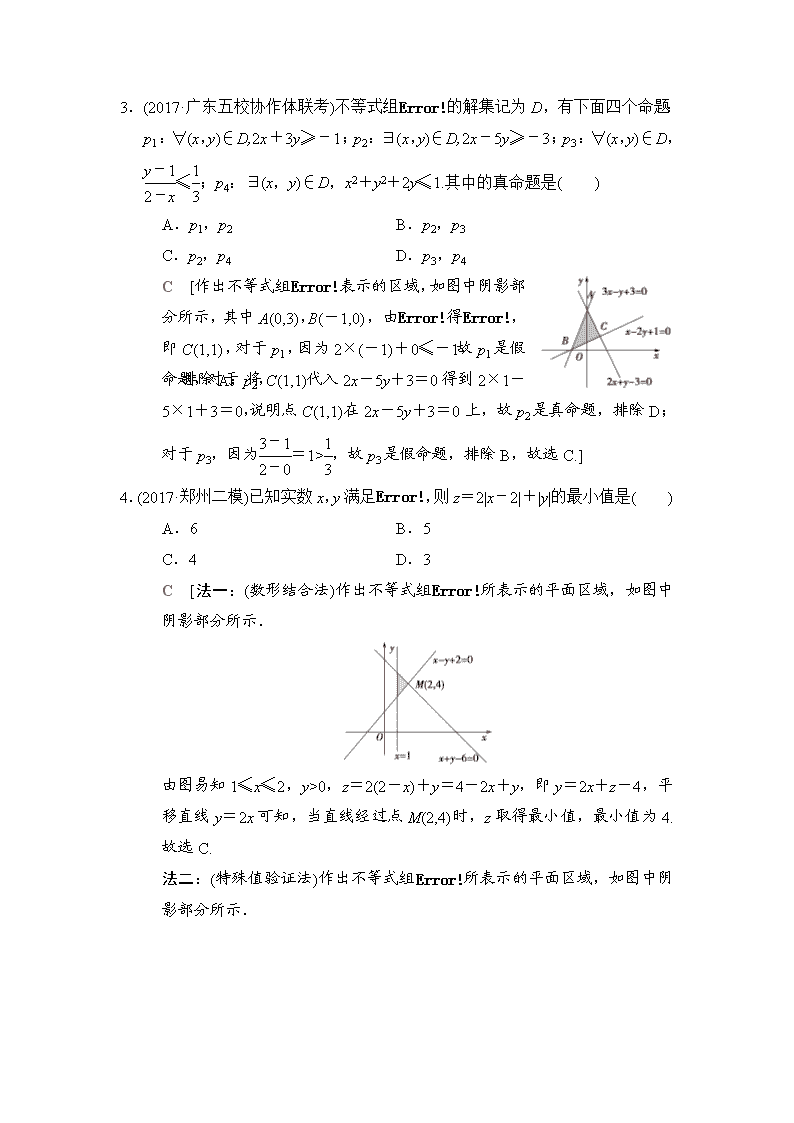
3.(2017·广东五校协作体联考)不等式组的解集记为D,有下面四个命题:p1:∀(x
,y)∈D,2x+3y≥-1;p2:∃(x,y)∈D,2x-5y≥-3;p3:∀(x,y)∈D,≤;p4:∃(x,y)∈D,x2+y2+2y≤1.其中的真命题是( )
A.p1,p2 B.p2,p3
C.p2,p4 D.p3,p4
C [作出不等式组表示的区域,如图中阴影部分所示,其中A(0,3),B(-1,0),由得,即C(1,1),对于p1,因为2×(-1)+0≤-1,故p1是假命题,排除A;对于p2,将C(1,1)代入2x-5y+3=0得到2×1-5×1+3=0,说明点C(1,1)在2x-5y+3=0上,故p2是真命题,排除D;对于p3,因为=1>,故p3是假命题,排除B,故选C.]
4.(2017·郑州二模)已知实数x,y满足,则z=2|x-2|+|y|的最小值是( )
A.6 B.5
C.4 D.3
C [法一:(数形结合法)作出不等式组所表示的平面区域,如图中阴影部分所示.
由图易知1≤x≤2,y>0,z=2(2-x)+y=4-2x+y,即y=2x+z-4,平移直线y=2x可知,当直线经过点M(2,4)时,z取得最小值,最小值为4.故选C.
法二:(特殊值验证法)作出不等式组所表示的平面区域,如图中阴影部分所示.
由可行域的形状可知,z=2|x-2|+|y|的最值必在顶点M(2,4),N(1,3),P(1,5)处取到,分别代入z=2|x-2|+|y|可得z=4或z=5或z=7,故选C.]
5.(2017·湘中名校模拟)若正数a,b满足:+=1,则+的最小值为( )
A.2 B.
C. D.1+
A [由a,b为正数,且+=1,得b=>0,所以a-1>0,所以+=+=+≥2=2,当且仅当=和+=1同时成立,即a=b=3时等号成立,所以+的最小值为2,故选A.]
6.(2017·石家庄模拟)已知函数f(x)=,则f(f(x))<2的解集为( )
A.(1-ln 2,+∞) B.(-∞,1-ln 2)
C.(1-ln 2,1) D.(1,1+ln 2)
B [因为当x≥1时,f(x)=x3+x≥2,当x<1时,f(x)=2ex-1<2,所以f(f(x))<2等价于f(x)<1,即2ex-1<1,解得x<1-ln 2,所以f(f(x))<2的解集为(-∞,1-ln 2),故选B.]
7.(2017·武昌区模拟)设x,y满足约束条件,且z=x+ay的最小值为7,则a=( )
A.-5 B.3
C.-5或3 D.5或-3
B [根据约束条件画出可行域如图1中阴影部分所示:
图1
可知可行域为开口向上的V字型.在顶点处z有最小值,顶点为,则+a=7,解得a=3或a=-5.当a=-5时,如图2,
图2
虚线向上移动时z减小,故z→-∞,没有最小值,故只有a=3满足题意.选B.]
8.(2017·河南、湖北、山西三省联考)已知实数x,y满足则z=的取值范围为( )
【导 号:07804126】
A. B.
C. D.
B [不等式组所表示的平面区域如图中阴影部分所示,z=表示点D(2,3)与平面区域内的点(x,y)之间连线的斜率.因点D(2,3)与B(8,1)连线的叙率为-且C的坐标为(2,-2),故由图知z=的取值范围为,故选B.
]
9.(2017·洛阳一模)已知实数x,y满足条件,若z=y-ax取得最大值时的最优解有且只有一个,则实数a的取值集合为( )
A.{2,-1} B.{a∈R|a≠2}
C.{a∈R|a≠-1} D.{a∈R|a≠2且a≠-1}
D [不等式组对应的平面区域如图中阴影部分所示.由z=-ax+y得y=ax+z,若a=0,直线y=ax+z=z,此时最大的最优解只有一个,满足条件.若a>0,则直线y=ax+z的纵截距最大时,z取得最大值,若z=y-ax取得最大值时的最优解有且只有一个,则a≠2.若a<0,则直线y=ax+z的纵截距最大时,z取得最大值,若z=y-ax取得最大值时的最优解有且只有一个,则a≠-1.选D.]
10.(2017·石家庄二模)在平面直角坐标系中,不等式组(r为常数)表示的平面区域的面积为π,若x,y满足上述约束条件,则z=的最小值为( )
A.-1 B.-
C. D.-
D [作出不等式组表示的平面区域,如图中阴影部分所示,由题意,知πr2=π,解得r=2.z==1+,表示可行域内的点与点P(-3,2)连线的斜率加上1,由图知当可行域内的点与点P的连线与圆相切时斜率最小.设切线方程为y-2=k(x+3),即kx-y+3k+2=0,则有=2,解得k=-或k=0(舍去),所以zmin=1-=-,故选D.]
11.(2017·郑州一模)设正实数x,y满足x>,y>1,不等式+≥m恒成立,则m的最大值为( )
A.2 B.4
C.8 D.16
C [依题意得,2x-1>0,y-1>0,+=+≥+≥4×2=8,即+≥8,当且仅当,即时,取等号,因此+的最小值是8,m≤8,m的最大值是8,选C.]
12.(2017·安徽师大附中模拟)当x,y满足不等式组时,-2≤kx-y≤2恒成立,则实数k的取值范围是( )
A.[-1,1] B.[-2,0]
C. D.
D [作出不等式组表示的平面区域,如图中阴影部分所示,设z=kx-y,由得,即B(-2,2),由得,即C(2,0),由得,即A(-5,-1),要使不等式-2≤kx-y≤2恒成立,则,
即,
所以-≤k≤0,故选D.]
二、填空题
13.(2017·全国Ⅰ卷)设x,y满足约束条件则z=3x-2y的最小值为________.
-5 [作出可行域如图阴影部分所示.
由z=3x-2y,得y=x-.
作出直线l0:y=x,并平移l0,知当直线y=x-过点A时,z取得最小值.
由得A(-1,1),
∴zmin=3×(-1)-2×1=-5.]
14.(2015·全国Ⅰ卷)若x、y满足约束条件则的最大值为________.
【导 号:07804127】
3 [画出可行域如图阴影所示,∵表示过点(x,y)与原点(0,0)的直线的斜率,
∴点(x,y)在点A处时最大.
由得
∴A(1,3).
∴的最大值为3.]
15.(2017·福州二模)已知实数x,y满足,若目标函数z=x+ay取得最小值的最优解有无数多个,则z=x+ay的最大值为________.
[作出不等式组所表示的平面区域如图中阴影部分所示,易得A(3,2),B(1,4),C.当a>0时,y=-x+z,作直线l0:y=-x,平移l0,易知当直线y=-x+z与4x+y-8=0重合时,z取得最小值的最优解有无数多个,此时a=,当直线过点A时,z取得最大值,且zmax=3+=;当a≤0时,数形结合知,目标函数z=x+ay取得最小值的最优解不可能有无数多个.综上所述zmax=.]
16.(2016·全国Ⅰ卷)某高 技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5 kg,乙材料1 kg,用5个工时;生产一件产品B需要甲材料0.5 kg,乙材料0.3 kg,用3个工时.生产一件产品A的利润为2
100元,生产一件产品B的利润为900元.该企业现有甲材料150 kg,乙材料90 kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为________元.
216 000 [设生产产品A为x件,产品B为y件,则
目标函数z=2 100x+900y.
作出可行域为图中的阴影部分(包括边界)内的整数点,图中阴影四边形的顶点坐标分别为(60,100),(0,200),(0,0),(90,0).
当直线z=2 100x+900y经过点(60,100)时,z取得最大值,zmax=2 100×60+900×100=216 000(元).]