2014高考数学题库精选核心考点大冲关专题演练28 直线与圆
考点28 直线与圆
【考点分类】
热点一 直线的方程与位置关系
1.【2013年普通高等学校统一考试试题新课标Ⅱ数学(理)卷】已知点A(-1,0);B(1,0),C(0,1),直线y=ax+b(a>0)将△ABC分割为面积相等的两部分,则b的取值范围是( )
(A)(0,1) (B)(1-,) ( C)(1-, (D)[,)
2.【2013年全国高考统一考试天津数学(文)卷】 已知过点P(2,2) 的直线与圆相切, 且与直线垂直, 则( )
(A) (B) 1 (C) 2 (D)
3.【2013年高考新课标Ⅱ数学(文)卷】 设抛物线C:y2=4x的焦点为F,直线过F且与C交于A, B两点.若|AF|=3|BF|,则的方程为( )[来源:学,科,网Z,X,X,K]
(A) y=x-1或y=-x+1 (B)y=(X-1)或y=(x-1)
(C)y=(x-1)或y=(x-1) (D)y=(x-1)或y=(x-1)
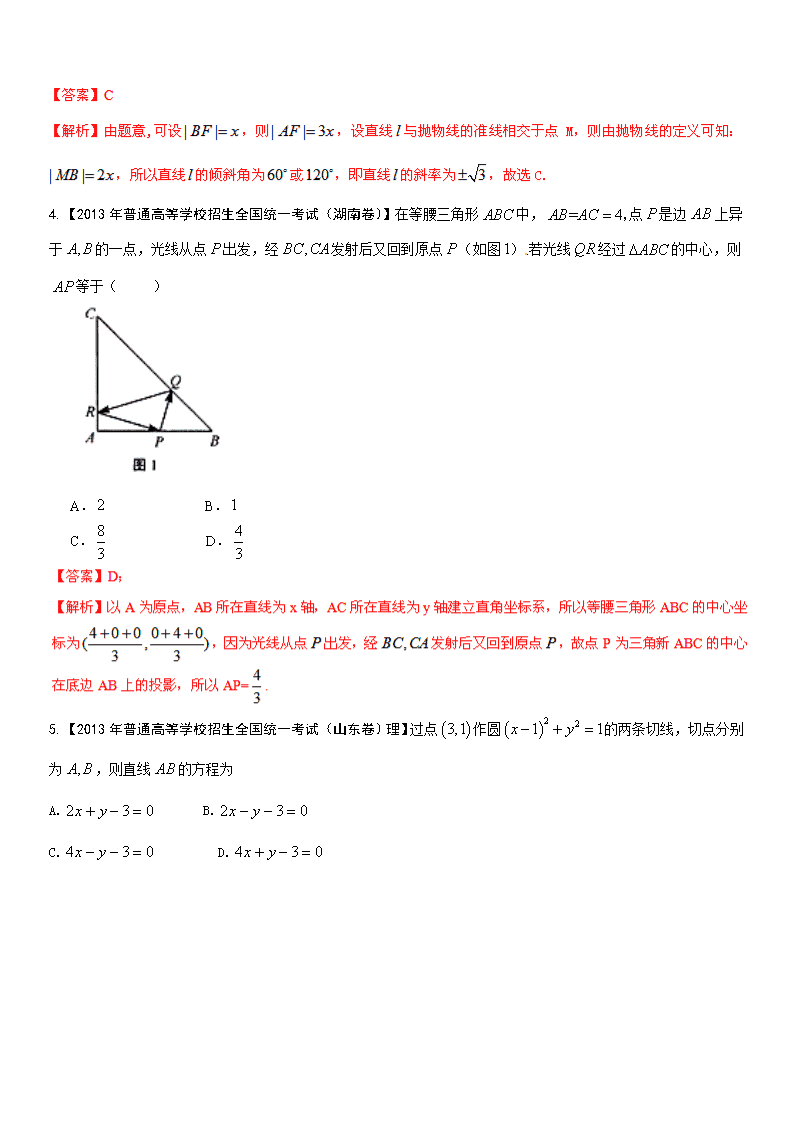
4.【2013年普通高等学校招生全国统一考试(湖南卷)】在等腰三角形中,点是边上异于的一点,光线从点出发,经发射后又回到原点(如图).若光线经过的中心,则等于( )
A. B.
C. D.
5.【2013年普通高等学校招生全国统一考试(山东卷)理】过点作圆的两条切线,切点分别为,则直线的方程为
A. B.
C. D.
6.【2013年普通高等学校招生全国统一考试(四川卷)文科】在平面直角坐标系内,到点,,,的距离之和最小的点的坐标是_______.
7.【2013年普通高等学校统一考试江苏数学试题】在平面直角坐标系中,设定点,是函数图象上一动点. 若点,之间的最短距离为,则满足条件的实数的所有值为
.
8.(2012年高考辽宁卷文科7)将圆x2+y2 -2x-4y+1=0平分的直线是( )
(A)x+y-1=0 (B) x+y+3=0 (C)x-y+1=0 (D)x-y+3=0
9.(2012年高考浙江卷理科3)设aR,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的( )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
10.(2012年高考湖北卷文科5)过点P(1,1)的直线,将圆形区域{(x,y)|x2+y2≤4}分两部分,使得这两部分的面积之差最大,则该直线的方程为 ( )
A.x+y-2=0 B.y-1=0 C.x-y=0 D.x+3y-4=0
【方法总结】
(1)充分掌握两直线平行与垂直的条件是解决本题的关键,对于斜率都存在且不重合的两条直线l1和l2,l1∥l2⇔k1=k2,l1⊥l2⇔k1·k2=-1.若有一条直线的斜率不存在,那么另一条直线的斜率是多少一定要特别注意.
(2)①若直线l1和l2有斜截式方程l1:y=k1x+b1,l2:y=k2x+b2,则:直线l1⊥l2的充要条件是k1·k2=-1.②设l1:A1x+B1y+C1=0,l2:A2x+B2y+C2=0.则:l1⊥l2⇔A1A2+B1B2=0.
热点二 圆的方程和性质
11.【2013年普通高等学校招生全国统一考试(江西卷)文科】若圆C经过坐标原点和点(4,0),且与直线y=1相切,则圆C的方程是 .
[答案]
[解析]由题意得圆心坐标为(2,y),半径r=1-y,则有则圆C的方程是
12.(2012年高考山东卷文科9)圆与圆的位置关系为( )
(A)内切 (B)相交 (C)外切 (D)相离
【答案】B
【解析】两圆的圆心分别为,,半径分别为,两圆的圆心距离为,则,所以两圆相交,选B.
13.(2012年高考新课标全国卷理科20)(本小题满分12分)
设抛物线的焦点为,准线为,,已知以为圆心,
为半径的圆交于两点;
(1)若,的面积为;求的值及圆的方程;
(2)若三点在同一直线上,直线与平行,且与只有一个公共点,
求坐标原点到距离的比值.
【方法总结】
1.利用圆的几何性质求方程:根据圆的几何性质,直接求出圆心坐标和半径,进而写出方程.
2.利用待定系数法求圆的方程:(1)若已知条件与圆的圆心和半径有关,则设圆的标准方程,依据已知条件列出关于a,b,r的方程组,从而求出a,b,r的值;
(2)若已知条件没有明确给出圆的圆心或半径,则选择圆的一般方程,依据已知条件列出关于D,E,F的方程 组,从而求出D,E,F的值.
热点三 直线与圆的位置关系
14.【2013年普通高等学校招生全国统一考试(广东卷)文科】垂直于直线且与圆相切于第一象限的直线方程是( )
A. B.
C. D.
15.【2013年普通高等学校招生全国统一考试(陕西卷) 文科】 已知点在圆外, 则直线与圆的位置关系是( )
(A) 相切 (B) 相交 (C) 相离 (D) 不确定
16.【2013年普通高等学校招生全国统一考试(江西卷)理】过点(,0)引直线ι与曲线 交于A,B两点 ,O为坐标原点,当△AOB的面积取最大值时,直线ι的斜率等于( )
A. B.- C. D-
17.(2012年高考广东卷文科8)在平面直角坐标系xOy中,直线3x+4y-5=0与圆x²+y²=4相交于A、B两点,则弦AB的长等于( )
A. B. C. D.1
18. (2012年高考天津卷理科8)设,,若直线与圆相切,则的取值范围是( )
(A) (B)
(C) (D)
19.(2012年高考陕西卷理科4)已知圆,过点的直线,则( )
(A)与相交 (B) 与相切 (C)与相离 (D) 以上三个选项均有可能
20.(2012年高考重庆卷理科3)对任意的实数k,直线y=kx+1与圆的位置关系一定是( )
A. 相离 B.相切 C.相交但直线不过圆心 D.相交且直线过圆心
21.【2013年普通高等学校招生全国统一考试(湖北卷)文科】已知圆:,直线:
().设圆上到直线的距离等于1的点的个数为,则 .
22.【2013年普通高等学校招生全国统一考试(山东卷)文科】过点(3,1)作圆的弦,其中最短的弦长为__________.
23.【2013年普通高等学校招生全国统一考试(浙江卷)文科】直线被圆所截得的弦长等于__________.
24.(2012年高考江西卷文科14)过直线x+y-=0上点P作圆x2+y2=1的两条切线,若两条切线的夹角是60°,则点P的坐标是__________.
25. (2012年高考天津卷文科12)设,若直线与轴相交于点A,与y轴相交于B,且l与圆相交所得弦的长为2,O为坐标原点,则面积的最小值为 .
.
26. (2012年高考江苏卷12)在平面直角坐标系中,圆C的方程为,若直线上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是 .
27.(2012年高考浙江卷理科16)定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y=x 2+a到直线l:y=x的距离等于C2:x 2+(y+4) 2 =2到直线l:y=x的距离,则实数a=______________.
.
28.【2013年普通高等学校统一考试江苏数学试题】如图,在平面直角坐标系中,点,直线
,设圆的半径为1, 圆心在上.
(1)若圆心也在直线上,过点作圆的切线,求切线方程;
(2)若圆上存在点,使,求圆心的横坐标的取值范围.
29.【2013年普通高等学校招生全国统一考试(四川卷)文科】已知圆的方程为,点是坐标原点.直线与圆交于、两点.
(Ⅰ)求的取值范围;
(Ⅱ)设是线段上的点,且.请将表示为的函数.
根据题意,点在圆内,则,所以,
于是与的函数关系为(). ……………………13分
【方法总结】
1.判断直线与圆的位置关系常见的有两种方法
(1)代数法:
(2)几何法:利用圆心到直线的距离d和圆半径r的大小关系:d
r⇔相离.
2.圆的弦长的常用求法
(1)几何法:设圆的半径为r,弦心距为d,弦长为l,则()2=r2-d2
(2)代数方法:运用韦达定理及弦长公式: |AB|=|x1-x2|=.注意:常用几何法研究圆的弦的有关问题.
3.求过一点的圆的切线方程时,首先要判断此点是否在圆上.然后设出切线方程,用待定系数法求解.注意斜率不存在情形.
【考点剖析】
一.明确要求
1.能根据两条直线的斜率判定这两条直线平行或垂直.
2.会求两直线的交点坐标.
3.掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.
4.掌握圆的标准方程和一般方程.
5.能判断直线与圆、圆与圆的位置关系.
6.能用直线和圆的方程解决一些简单的问题.
二.命题方向
1.两条直线的平行与垂直,点到直线的距离,两点间距离是命题的热点.对于距离问题多融入解答题中,注重考查分类讨论与数形结合思想.题型多为客观题,难度中低档.
2.求圆的方程或已知圆的方程求圆心坐标,半径是高考的热点,多与直线相结合命题,着重考查待定系数法求圆的方程,同时注意方程思想和数形结合思想的运用.多以选择题、填空题的形式出现,属中、低档题.
3.直线与圆的位置关系,特别是直线与圆相切一直是高考考查的重点和热点.多以选择题和填空题的形式出现,有时也出现在综合性较强的解答题中.
三.规律总结
一条规律
与直线Ax+By+C=0(A2+B2≠0)平行、垂直的直线方程的设法:
一般地,平行的直线方程设为Ax+By+m=0;垂直的直线方程设为Bx-Ay+n=0.
两个防范
(1)在判断两条直线的位置关系时,首先应分析直线的斜率是否存在.两条直线都有斜率,可根据判定定理判断,若直线无斜率时,要单独考虑.[来源:学§科§网]
(2)在运用两平行直线间的距离公式d=时,一定要注意将两方程中的x,y系数化为分别相等.
三种对称
(1)点关于点的对称
点P(x0,y0)关于A(a,b)的对称点为P′(2a-x0,2b-y0).
(2)点关于直线的对称
设点P(x0,y0)关于直线y=kx+b的对称点P′(x′,y′),
则有可求出x′,y′.
(3)直线关于直线的对称
①若已知直线l1与对称轴l相交,则交点必在与l1对称的直线l2上,然后再求出l1上任一个已知点P1关于对称轴l对称的点P2,那么经过交点及点P2的直线就是l2;②若已知直线l1与对称轴l平行,则与l1对称的直线和l1分别到直线l的距离相等,由平行直线系和两条平行线间的距离即可求出l1的对称直线.
一种方法
确定圆的方程主要方法是待定系数法,大致步骤为:
(1)根据题意,选择标准方程或一般方程;
(2)根据条件列出关于a,b,r或D、E、F的方程组;
(3)解出a、b、r或D、E、F代入标准方程或一般方程.
两个防范
(1)求圆的方程需要三个独立条件,所以不论设哪一种圆的方程都要列出关于系数的三个独立方程.
(2)过圆外一定点求圆的切线,应该有两个结果,若只求出一个结果,应该考虑切线斜率不存在的情况.
三个性质
确定圆的方程时,常用到的圆的三个性质
(1)圆心在过切点且与切线垂直的直线上;
(2)圆心在任一弦的中垂线上;
(3)两圆内切或外切时,切点与两圆圆心三点共线.
一条规律
过圆外一点M可以作两条直线与圆相切,其直线方程可用待定系数法,再利用圆心到切线的距离等于半径列出关系式求出切线的斜率即可.
一个指导
直线与圆的位置关系体现了圆的几何性质和代数方法的结合,“代数法”与“几何法”是从不同的方面和思路来判断的,“代数法”侧重于“数”,更多倾向于“坐标”与“方程”;而“几何法”则侧重于“形”,利用了图形的性质.解题时应根据具体条件选取合适的方法.
两种方法
计算直线被圆截得的弦长的常用方法
(1)几何方法
运用弦心距(即圆心到直线的距离)、弦长的一半及半径构成直角三角形计算.
(2)代数方法
运用根与系数关系及弦长公式
|AB|=|xA-xB|
=.
说明:圆的弦长、弦心距的计算常用几何方法.
【考点模拟】
一.扎实基础
1.【湖北省黄冈市黄冈中学2013届高三五月第二次模拟考试】 “”是“直线垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.【2013安徽省省级示范性高中名校高三联考】已知圆的一条切线是,则k=( )
A. B. C.或 D.
3.【山东省济南市2013届高三高考第一次模拟考试】已知两条直线,平行,则( )
A.-1 B.2
C.0或-2 D.-1或2
4.【2013年“江南十校”高三学生第二次联考(二模)测试】若双曲线的渐近线与圆相切,则( )
A.2 B. C. D.
5.【安徽省江淮名校2013届高考最后一卷文科数学】直线与圆在第一象限内有两个不同的交点,则m取值范围是( )
A. B. C. D.
线)之间.
6.【天津市新华中学2013届高三上学期第三次月考数学试卷】倾斜角为135°,在轴上的截距为的直线方程是( )
A. B.
C. D.
7. 【2013年山东省日照市高三模拟考试】若PQ是圆的弦,PQ的中点是(1,2)则直线PQ的方程是( )
A. B.
C. D.
8.【湖北省黄冈市黄冈中学2013届高三下学期6月适应性考试】圆:的圆心到直线3x+4y+14=0的距离是 .
9.【浙江省镇海中学2013年高三考前模拟】若圆C:与轴有公共点,则的取值范围是________.
10. 【广东省揭阳市2013届高三3月第一次高考模拟】已知圆C经过直线与坐标轴的两个交点,且经过抛物线的焦点,则圆C的方程为 .
二.能力拔高
11.【2013年长春市高中毕业班第四次调研测试】已知直线:,若以点为圆心的圆与直线相切于点,且在轴上,则该圆的方程为( )
A. B.
C. D.
12.【山东省烟台市2013届高三第一次模拟诊断性测试】已知抛物线y2 =2px(p>0)上一点M(1,m)(m>0)到其焦点F的距离为5,则以M为圆心且与y轴相切的圆的方程为( )
A.(x-1)2+(y-4)2=1 B.(x-1)2+(y+4)2=1
C.(x-l)2+(y-4)2 =16 D.(x-1)2+(y+4)2=16
13.【山东省济南市2013届高三高考第一次模拟考试】已知直线与圆相交于两点,且 则 的值是( )
A. B. C. D.0
14.【2013年云南省第二次高中毕业生复习统一检测】已知⊙的半径等于,圆心是抛物线的
焦点,经过点的直线将⊙分成两段弧,当优弧与劣弧之差最大时,直线的方程为( )
(A) (B)
(C) (D)
15.【江西省南昌市2013届二模考试】已知点内任意一点,点是圆上任意一点,则实数( )
A.一定是负数 B.一定等于0
C.一定是正数 D.可能为正数也可能为负数
【答案】A
【解析】令,
,又因为小于1,所以必定是负数,故选A。
16.【山东省临沂市2013届高三5月高考模拟】若函数的图象在处的切线与圆相切,则的最大值是( )
(A)4 (B) (C)2 (D)
17.【浙江省嘉兴市2013届高三4月教学测试】已知点和圆:,是圆的直径,和是的三等分点,(异于)是圆上的动点,于,,直线与交于,则当 时,为定值.
【答案】.
【解析】设,则,…①
…② 由①②得,
将代入,得.由,得到.
18.【成都龙泉驿区2013届5月高三数学押题试卷】已知D是由不等式组所确定的平面区域,则圆+=4在区域D内的弧长为________.
【答案】
【解析】作出可行域D及圆+=4如图所示,图中阴影部分所在圆心角=+所对的弧长即为所求.易
19.【浙江省宁波市2013年高考模拟押题试卷】在直角坐标平面上,已知点A(0,2),B(0,1),D(t,0)(t>0).点M是线段AD上的动点,如果|AM|≤2|BM|恒成立,则正实数t的最小值是 .
20.【成都龙泉驿区2013届5月高三数学押题试卷】直线ax+by+c=0与圆+=9相交于两点M、N,若c2=a2+b2,则· (O为坐标原点)等于________.
三.提升自我
21. 【江西省2013年四月高中毕业班新课程教学质量监测卷】直线ax+2by =1与圆x2 +y2 =1相交于A,B两点(其中a,b是实数),且ΔAOB是直角三角形(0是 坐标原点),则点P(a,b)与点Q(0,1)之间距离的最大值为
A . 3 B. C. D .
【答案】D[来源:学科网ZXXK]
【解析】由圆可知圆心为(0,0),半径为1,所以则是等腰直角三角形,得到
22. 【山东省潍坊市2013届高三第二次模拟考试】已知抛物线与圆有公共的切线,则_____.
23.【江苏省常州市金坛四中2013年高考数学冲刺模拟】已知圆C:x2+y2+2x-4y+3=0.
(1)若圆C的切线在x轴和y轴上的截距相等,求此切线的方程;
(2)从圆C外一点P(x1,y1)向该圆引一条切线,切点为M,O为坐标原点,且有|PM|=|PO|,求使得|PM|取得最小值时点P的坐标.
24.【扬州、南通、泰州、宿迁四市2013届高三第二次调研测试数学试卷】在平面直角坐标系xOy中,已知圆C:x2+y2=r2和直线l:x=a(其中r和a均为常数,且0 < r < a),M为l上一动点,A1,A2为圆C与x轴的两个交点,直线MA1,MA2与圆C的另一个交点分别为P、Q.
(1)若r=2,M点的坐标为(4,2),求直线PQ方程;
(2)求证:直线PQ过定点,并求定点的坐标.
25.【虹口区2013届高三一模】已知圆.
(1)直线:与圆相交于、两点,求;
(2)如图,设、是圆上的两个动点,点关于原点的对称点为,点关于轴的对称点为,如果直线、与轴分别交于和,问是否为定值?若是求出该定值;若不是,请说明理由.
解:(1)圆心到直线的距离.
圆的半径,.………………4分
(2),,则,,,.………………8分
:,得.
:,得.…………12分[来源:学科网]
………………14分[
【考点预测】
1. 已知直线,且于,为坐标原点,
则点的轨迹方程为 ( )
A. B. C. D.
2. 已知P(x,y)是直线上一动点,PA,PB是圆
C:的两条切线, A. B是切点,若四边形PACB的最小面积是2,则的值为 ( )
A.3 B. C. D.
3. 在平面直角坐标系中,设点为圆:上的任意一点,点(2,) (),则线段长度的最小值为 .
4. 已知集合,集合
,若,则实数可以取的一个值是 ( )
A. B. C. D.
显然,,故只有A.项满足.
5. 圆的方程为,圆的方程,过上任意一点P作圆的两条切线PM、PN,切点分别为M、N,则∠MPN最大值为_____________.
[来源:学§科§网Z§X§X§K]