2020届二轮复习正弦定理课件（12张）（全国通用）

2020届二轮复习正弦定理课件（12张）（全国通用）

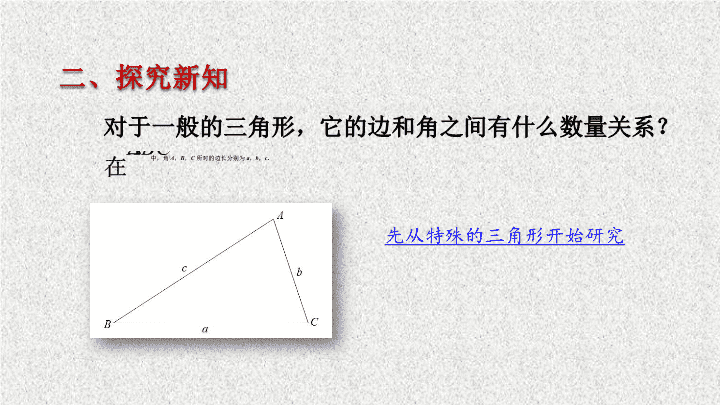
某沿海城市防汛减灾指挥中心收到气象部门的台风预警：台风中心位于该市正东方向300 km 处,正以40 km / h 的速度向西北方向移动,距离台风中心250 km 范围内将会受到影响.如果台风风速不变,那么该城市从何时起要遭受台风影响?这种影响会持续多长时间? 动态演示 一、情境导入 二、探究新知 对于一般的三角形，它的边和角之间有什么数量关系？ 先从特殊的三角形开始研究 三、定理生成 利用三角函数的定义证明 学生展示探究成果 点评：该方法充分利用三角函数的定义、诱导公式等现有知识解决问题，将复杂问题转化为简单问题，将未知问题转化为已知问题。 三、定理生成 利用等面积法证明 学生展示探究成果 点评：不仅达到了证明的目的，而且还得到了三角形面积计算公式。 三、定理生成 利用外接圆证明 学生展示探究成果 点评：不仅达到了证明的目的，而且三角形边与对角正弦值之比的几何意义 —— 三角形外接圆半径的 2 倍（直径）。 三、定理生成 学生思考教师证明方法中的漏洞 b c （ A ） B a C O x y 利用平面向量证明 定理的作用： 1. 已知两边及其中一边的对角，求其余的边和角； 2. 已知两角及任意一边，求其余的边和角 . 关于正弦定理的发现历史，一般认为是中世纪阿拉伯数学家、天文学家阿布瓦法（ Abul-Wefa ， 940~998 ）提出并证明了球面三角形的正弦定理，而平面三角形的正弦定理的证明最先是纳绥尔丁 - 图西（ Nasiral-Dinal-Tusi,1201~1274 ）给出的。我国清代数学家梅文鼎（ 1633~1721 ）在他的著作 《 平三角举要 》 中也给出了证明，而且还给出了正弦定理的完整形式。 阿布瓦法 纳绥尔丁 - 图西 梅文鼎 四、定理应用 某沿海城市防汛减灾指挥中心收到气象部门的台风预警：台风中心位于该市正东方向300 km 处,正以40 km / h 的速度向西北方向移动,距离台风中心250 km 范围内将会受到影响.如果台风风速不变,那么该城市从何时起要遭受台风影响?这种影响会持续多长时间? 一般来说，台风侵袭的范围（圆形区域）的半径会不断增大，本题没有考虑这个因素，如果考虑侵袭范围的变化，怎么办？大家课后思考 . 五、随堂练习 B E D C A B E D C