2019年高考数学高分突破复习课件考前冲刺三 第二类

2019年高考数学高分突破复习课件考前冲刺三 第二类

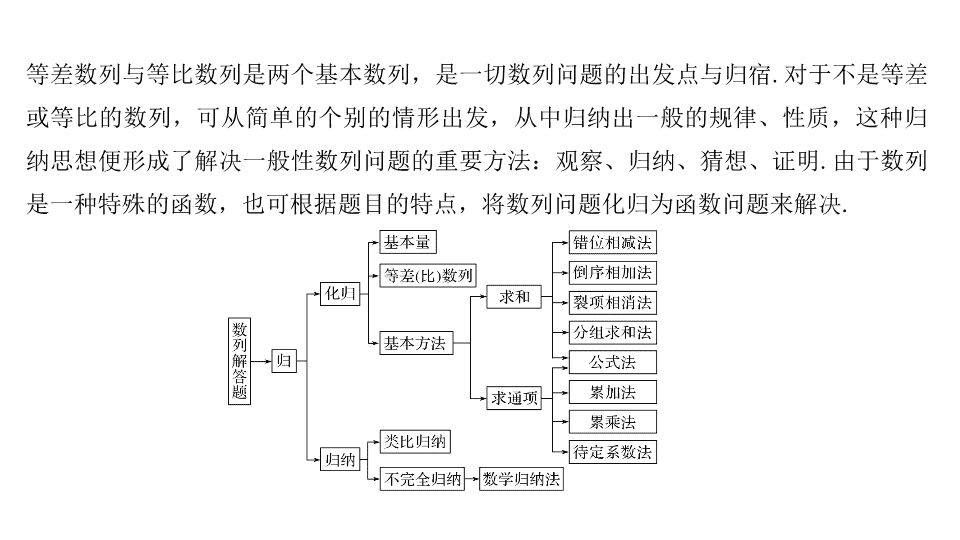
第二类　数列问题重在 “ 归 ” —— 化归、归纳 等差数列与等比数列是两个基本数列，是一切数列问题的出发点与归宿 . 对于不是等差或等比的数列，可从简单的个别的情形出发，从中归纳出一般的规律、性质，这种归纳思想便形成了解决一般性数列问题的重要方法：观察、归纳、猜想、证明 . 由于数列是一种特殊的函数，也可根据题目的特点，将数列问题化归为函数问题来解决 . 【例 2 】 (2017· 全国 Ⅲ 卷 ) 设数列 { a n } 满足 a 1 ＋ 3 a 2 ＋ … ＋ (2 n － 1) a n ＝ 2 n . 又 n ＝ 1 时， a 1 ＝ 2 适合上式， 解　 (1) 因为 a 1 ＋ 3 a 2 ＋ … ＋ (2 n － 1) a n ＝ 2 n ， 当 n ≥ 2 时， a 1 ＋ 3 a 2 ＋ … ＋ (2 n － 3) a n － 1 ＝ 2( n － 1) . ( 归纳 ) 探究提高 　 1.(1) 归纳：通过条件归纳出 a 1 ＋ 3 a 2 ＋ … ＋ (2 n － 3) a n － 1 ＝ 2( n － 1)( n ≥ 2) ，进而得出 { a n } 的通项公式 . (2) 化归：把数列的通项分拆，利用裂项相消法求和 . 2 . 破解策略： “ 算一算、猜一猜、证一证 ” 是数列中特有的归纳思想，利用这种思想可探索一些一般数列的简单性质 . 等差数列与等比数列是数列中的两个特殊的基本数列，高考中通常考查的是非等差、等比数列问题，应对的策略就是通过化归思想，将其转化为这两种数列 . 当 n ≥ 2 时， S n ＝ λS n － 1 ＋ λ ， a n ＋ 1 ＝ S n ＋ 1 － S n ＝ λ ( S n － S n － 1 ) ＝ λa n ， 故数列 { a n } 是首项为 λ ，公比为 λ 的等比数列 .