2018届二轮复习幂函数课件（全国通用）

2018届二轮复习幂函数课件（全国通用）

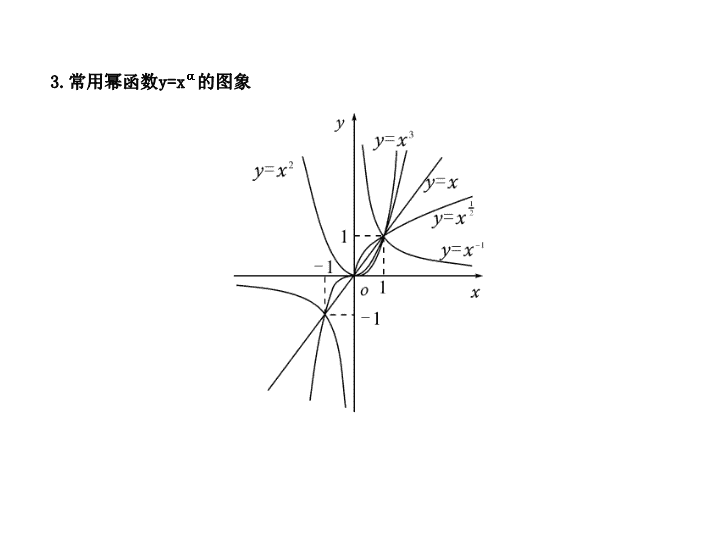
第三章　函 数 第 7 节 幂函数 1. 幂函数的定义 一般地 , 形如 y=x α (α∈R) 的函数称为幂函数 , 其中 α 为常数 . 2. 幂函数 y=x α (α≠0,1) 在第一象限的图象 3. 常用幂函数 y=x α 的图象 4. 观察图象 , 总结填写下表 : 【 例 1 】 函数 f ( x )=( x -1) α +2 过定点 ( ) A.(1,3) B.(1,2) C.(2,3) D.(0,1) 【 答案 】 　 C 【 解析 】 当 x -1=1 时 , 无论 α 取什么值 , 都有 ( x -1) α =1, 解得 x =2, y =3,∴ 函数 f ( x )=( x -1) α +2 过定点 (2,3). 2. 若幂函数 f ( x )= x m -1 在 (0,+∞) 上是增函数 , 则 ( ) A. m >1 B. m <1 C. m =1 D. 不能确定 【 答案 】 A 【 解析 】 要幂函数 f ( x )= x m -1 在 (0,+∞) 上是增函数 , 只要 m -1>0, 得到 m >1, 选 A. 8. 如图是幂函数 y = x m 与 y= x n 在第一象限内的图象 , 则 ( ) A.-1< n <0< m <1 B. n <-1,0< m <1 C.-1< n <0, m >1 D. n <-1, m >1 10. 已知幂函数 f ( x )= ( m ∈ Z ) 为偶函数 , 且在区间 (0,+∞) 上是单调增函数 . 则函数 f ( x ) 的解析式为 . 【 答案 】 f ( x )= x 4 【 解析 】 ∵ f ( x ) 在区间 (0,+∞) 上是单调增函数 ,∴- m 2 +2 m +3>0, 即 m 2 -2 m -3<0, 解得 -1< m <3. 又 m ∈Z,∴ m =0,1,2, 而当 m =0,2 时 , f ( x )= x 3 不是偶函数 ; 当 m =1 时 , f ( x )= x 4 是偶函数 . 故函数 f ( x ) 的解析式为 f ( x )= x 4 . 12. 为了保证信息的安全传输 , 有一种为秘密密钥密码系统 , 其加密、解密原理为 : 发送方由明文到密文 ( 加密 ), 接收方由密文到明文 ( 解密 ). 现在加密密钥为 y = x α ( α 为常数 ), 如“ 4” 通过加密后得到密文“ 2”. 若接收方接到密文“ 3”, 则解密后得到的明文是 . 【 答案 】 D 【 解析 】 构造幂函数 y = (x∈R), 由该函数在定义域内单调递增 , 知 a > b ; 构造指数函数 y = , 由该函数在定义域内单调递减 , 所以 a < c , 故 c > a > b . 【 答案 】 B 【 解析 】 由于 >1, 故可排除选项 A 、 D. 根据幂函数的性质可知 , 当 α >1 时 , 幂函数的图象在第一象限内下凸 , 故排除选项 C, 只有选项 B 正确 .