2017-2018学年黑龙江省齐齐哈尔市第八中学高二下学期期中考试数学（理）试题 Word版

2017-2018学年黑龙江省齐齐哈尔市第八中学高二下学期期中考试数学（理）试题 Word版

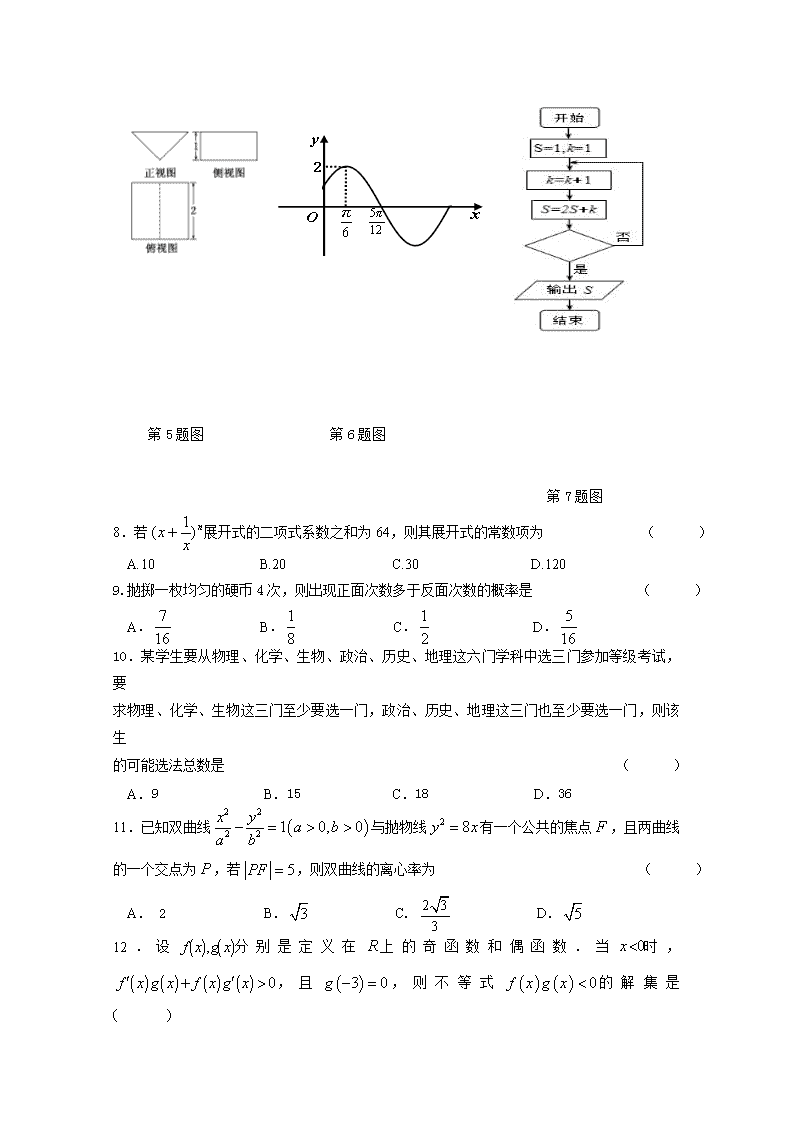
‎ 2017-2018学年度黑龙江省齐齐哈尔市第八中学下学期期中考试 高二数学(理科)试题 Ⅰ 选择题（共60分）‎ 一、选择题:本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1．设集合，集合，则 （ ）‎ ‎ A． B． C． D．‎ ‎2.设复数满足，则 （ ）‎ ‎ A． B． C． D．2‎ ‎3．甲、乙两人各进行一次射击，甲击中目标的概率是，乙击中目标的概率是，则恰有一人击中目标的概率是 （　　 ）‎ ‎ A． B． C． D．‎ ‎4．等于 （　 　）‎ ‎ A． B． 2 C． D． ‎ ‎5.《九章算数》中，将底面是直角三角形的直三棱柱称为“堑堵”，已知某“堑堵”的三视图如图所示，俯视图中虚线平分矩形的面积，则该“堑堵”的侧面积为 （ ）‎ ‎ A．2 B． C． D．‎ ‎ 6.已知函数的部分图象如图所示，则函数的解析式为 （ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎7.某程序框图如图所示，若输出的，则判断框内为 （　　 ）‎ A．？ B．？ C．？ D．？‎ ‎ 第5题图 第6题图 ‎ ‎ 第7题图 ‎8．若展开式的二项式系数之和为64，则其展开式的常数项为 （ ）‎ ‎ A.10 B.20 C.30 D.120‎ ‎9.抛掷一枚均匀的硬币4次，则出现正面次数多于反面次数的概率是 （　　 ）‎ ‎ A． B． C． D．‎ ‎10．某学生要从物理、化学、生物、政治、历史、地理这六门学科中选三门参加等级考试，要 求物理、化学、生物这三门至少要选一门，政治、历史、地理这三门也至少要选一门，则该生 的可能选法总数是 （　 　）‎ ‎ A．9  B．15   C．18   D．36‎ ‎11．已知双曲线与抛物线有一个公共的焦点，且两曲线的一个交点为，若，则双曲线的离心率为 （ ）‎ ‎ A． 2 B． C. D．‎ ‎12．设分别是定义在上的奇函数和偶函数．当时，，且，则不等式的解集是 (　　 )‎ ‎ A． B．‎ ‎ C． D． ‎ ‎ Ⅱ 非选择题（共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20 分.请将正确答案填在答题卡的横线上.‎ ‎13.不等式的解集为 ；‎ ‎14．，满足约束条件，则的最大值为 ；‎ ‎15．设,则的值 为 ；‎ ‎16．小明跟父母、爷爷、奶奶一同参加《中国诗词大会》的现场录制，5人坐成一排．若小明的父母至少有一人与他相邻，则不同坐法的总数为 ；‎ 三、解答题：本大题共6小题，共70分.解答题应写出文字说明、证明过程或演算步骤.‎ ‎17. （本小题满分10分）已知在平面直角坐标系中，直线的参数方程是（‎ 是参数），以原点为极点，轴正半轴为极轴且取相同的单位长度建立极坐标系，曲线的极坐标方程为．‎ ‎（I）求直线的普通方程与曲线的直角坐标方程；‎ ‎（Ⅱ）设为曲线上任意一点，求的取值范围．‎ ‎18. （本小题满分12分）从4名男生和2名女生中任选3人参加演讲比赛，设随机变量表 示所选3人中女生的人数.‎ ‎（I）求随机变量的分布列 ‎（Ⅱ）求“所选3人中女生人数”的概率.‎ ‎19．（本小题满分12分）已知数列为递增的等比数列， ，.‎ ‎（I）求数列的通项公式；‎ ‎（Ⅱ）记，求数列的前项和.‎ ‎20．（本小题满分12分）如图， 在三棱柱中，侧面是矩形，，，.‎ ‎（I）求证：⊥平面；‎ ‎（Ⅱ）设分别为的中点，求二面角的大小的余弦值．‎ ‎21.（本小题满分12分）据统计，2017年国庆中秋假日期间， 黔东南州共接待游客590.23万人次，实现旅游收入48.67亿元，同比分别增长44.57%、55.22%.旅游公司规定：若公司导游接待旅客，旅游年总收入不低于40（单位：百万元），则称为优秀导游.经验表明，如果公司的优秀导游率越高，则该公司的影响度越高.已知甲、乙两家旅游公司各有导游100名，统计他们一年内旅游总收入，分别得到甲公司的频率分布直方图和乙公司的频数分布表如下：‎ 分组 频数 ‎18‎ ‎49‎ ‎24‎ ‎5‎ ‎（I）求的值，并比较甲、乙两家旅游公司，哪家的影响度高?‎ ‎（Ⅱ）若导游的奖金（单位：万元），与其一年内旅游总收入（单位：百万元）之间的关系 为，求甲公司导游的年平均奖金；‎ ‎（Ⅲ）从甲、乙两家公司旅游收入在的总人数中，随机的抽取人进行表彰，设来自乙公司的人数为，求的分布列及数学期望.‎ ‎22．(本题满分12分) 已知函数 ‎ ‎ (I)当时，求曲线在处的切线方程；‎ ‎ (Ⅱ)当时，判断在上的单调性，并说明理由；‎ ‎ (Ⅲ)当时，求证：，都有．‎ 数学参考答案（理科） ‎ 一、本题共12小题，每小题5分，共60分.‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B B A A ‎ C ‎ D ‎ A B ‎ D C A D 二、本题共4小题，每小题5分，共20分.‎ ‎13. 14. 3 15. 1 16. 84‎ 三、 17. （I）由，得，故直线的普通方程为，‎ 由，得，所以，即，‎ 故曲线的普通方程为； ……5分 ‎（Ⅱ）据题意设点，则，‎ 所以的取值范围是． ……10分 ‎18. 解：（I）‎ X ‎0‎ ‎1‎ ‎2‎ P ‎ ………………6分 ‎（Ⅱ） ………………12分19（Ⅰ）由及得或（舍）‎ 所以，所以 ……6分 ‎（Ⅱ）由（Ⅰ）得所以 ……12分 ‎ 20. 解：（I）在三棱柱ABC－A1B1C1中，侧面ABB1A1是矩形，∴AA1⊥AB，又AA1⊥BC，AB∩BC＝B，∴A1A⊥平面ABC，∴A1A⊥AC.又A1A＝AC，∴A1C⊥AC1.又AB⊥AC. AB⊥AA1 , AC∩AA1＝A，∴AB⊥平面A1ACC1又A1C⊂平面A1ACC1，∴A1C⊥AB又AB∩AC1＝A∴A1C⊥平面ABC1 ……6分 ‎ ‎（Ⅱ）以A为坐标原点，AB，AC，AA1所在的直线分别为x轴、y轴、z轴建立空间直角坐标系， 因为AA1＝AC＝2AB＝4，∴A(0,0,0)，B(2,0,0)，C1(0,4,4)，C(0,4,0)，E(2,0,2)，A1(0,0,4)，由(1)知，＝(0,4，－4)是平面ABC1的一个法向量．设n＝(x，y，z)为平面AC1E的法向量，‎ ‎∵＝(0,4,4)，＝(2,0,2)，∴即 令z＝1，则x＝－1，y＝－1，∴n＝(－1，－1,1)为平面AC1E的一个法向量．‎ 设与n的夹角为θ，则cosθ＝＝－，由图知二面角E－AC1－B为锐角，‎ ‎∴二面角E－AC1－B的余弦值为. ……12分 ‎21.（I）由直方图知：，有，‎ 由频数分布表知：，有．‎ 甲公司的导游优秀率为：；乙公司的导游优秀率为：；由于，所以甲公司的影响度高． …………………4分 ‎（Ⅱ）甲公司年旅游总收入的人数为人；年旅游总收入的人数为人；年旅游总收入的人数人；故甲公司导游的年平均奖金（万元）． ………………8分 ‎（Ⅲ）由已知得，年旅游总收入在的人数为15人，其中甲公司10人，乙公司5人．故的可能取值为，易知： ； ； ； . 的分布列为：‎ ‎ 的数学期望为：‎ ‎． …………12分 ‎22. （Ⅰ）当时，,.得又,所以曲线在处的切线方程为 ………….…4分 ‎（Ⅱ）因为，所以. ‎ 令， 则 ， ‎ 随x的变化情况如下表：‎ x ‎+‎ 极大值 当时，.所以时，，即，‎ 所以在区间单调递增. .…………………….…8分 ‎（Ⅲ）由（Ⅱ）可知，当时，在区间单调递增，所以时，. 当时，设，则 ‎ ‎，随x的变化情况如下表：‎ x ‎+‎ 极大值 所以在上单调递增，在上单调递减 因为，‎ ‎，所以存在唯一的实数，使得，且当时，，当时，，所以在上单调递增，在上单调递减.又 ，,‎ 所以当时，对于任意的，. ‎ 综上所述，当时，对任意的，均有. .…………………….…12分