【数学】2021届一轮复习人教A版简单几何体的外接球和内切球问题的基本解法

【数学】2021届一轮复习人教A版简单几何体的外接球和内切球问题的基本解法

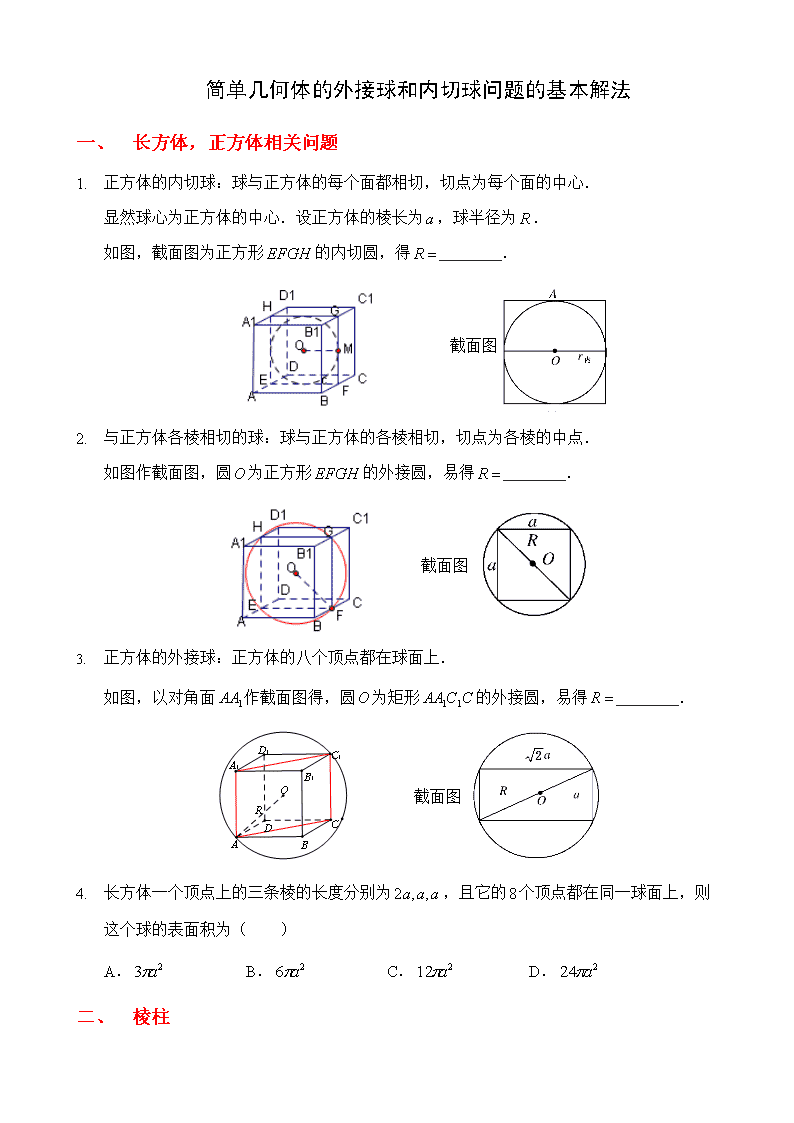
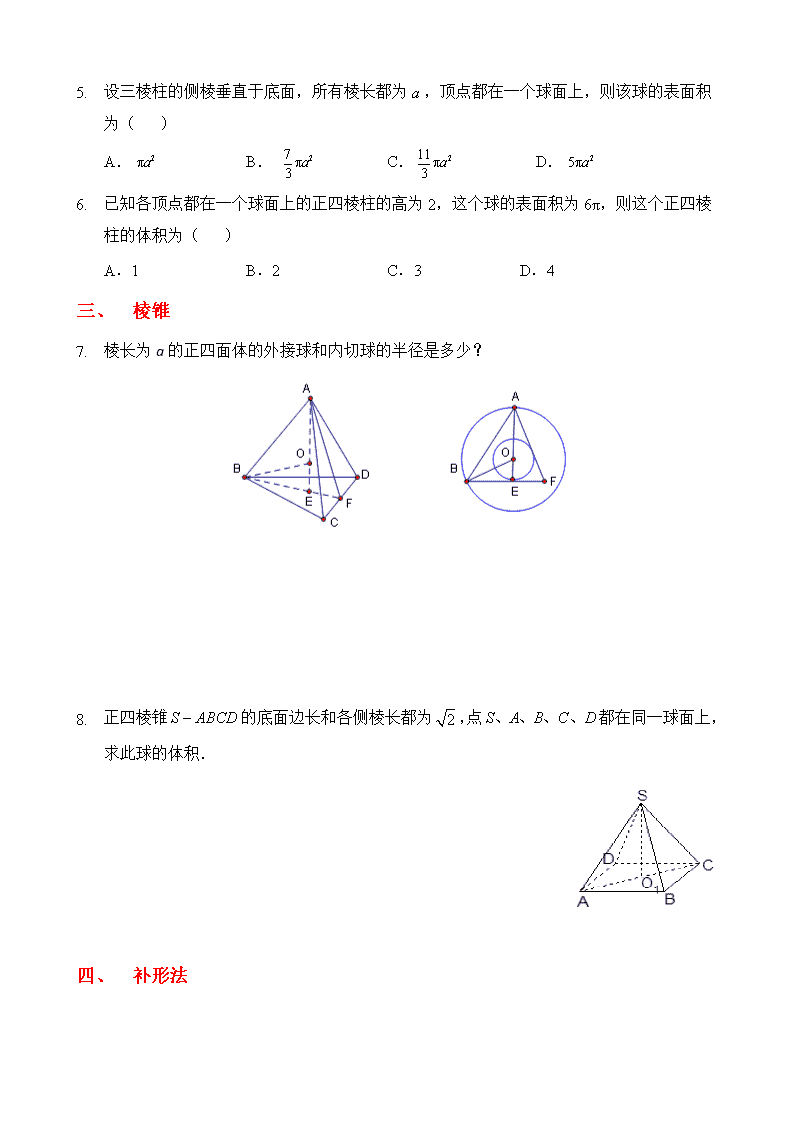
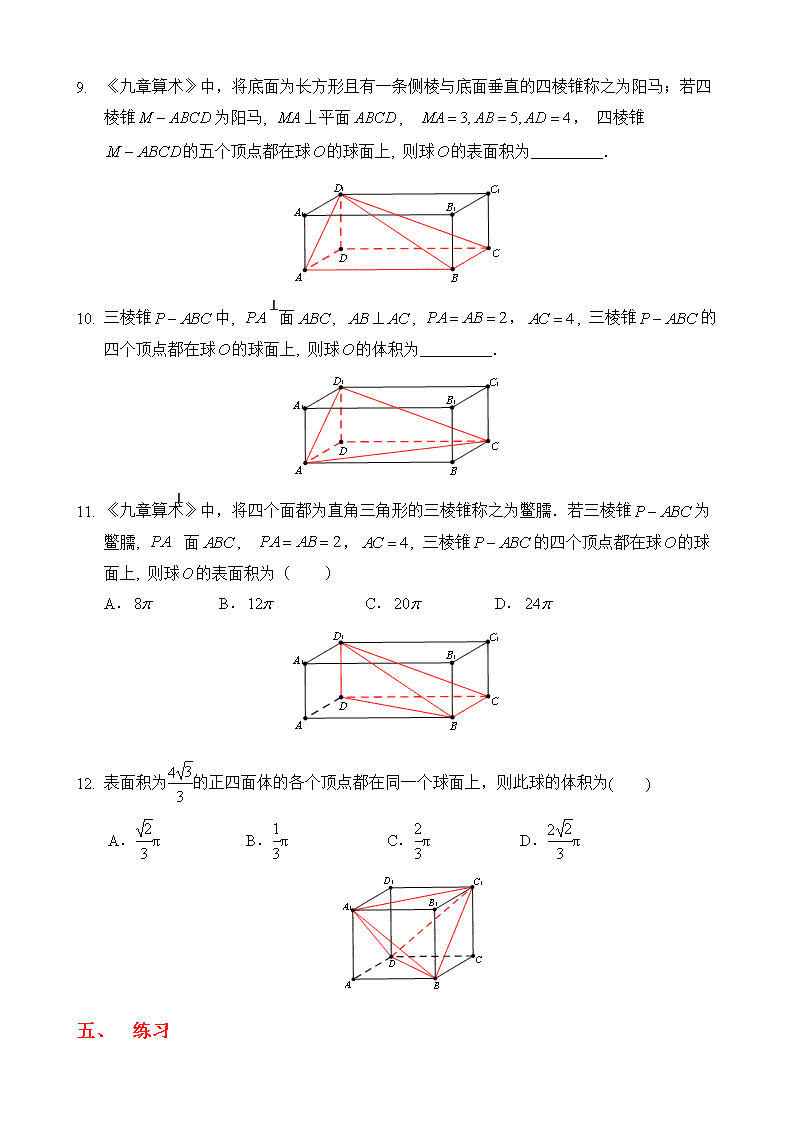
简单几何体的外接球和内切球问题的基本解法 一、 长方体，正方体相关问题 1. 正方体的内切球：球与正方体的每个面都相切，切点为每个面的中心．‎ 显然球心为正方体的中心．设正方体的棱长为，球半径为．‎ 如图，截面图为正方形的内切圆，得_________．‎ ‎ 截面图 2. 与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点．‎ 如图作截面图，圆为正方形的外接圆，易得_________．‎ ‎ 截面图 3. 正方体的外接球：正方体的八个顶点都在球面上．‎ 如图，以对角面作截面图得，圆为矩形的外接圆，易得_________．‎ ‎ 截面图 4. 长方体一个顶点上的三条棱的长度分别为，且它的个顶点都在同一球面上，则这个球的表面积为（ ）‎ A． B． C． D．‎ 二、 棱柱 1. 设三棱柱的侧棱垂直于底面，所有棱长都为，顶点都在一个球面上，则该球的表面积为（ ）‎ A． B． C． D．‎ 2. 已知各顶点都在一个球面上的正四棱柱的高为2，这个球的表面积为6π，则这个正四棱柱的体积为（ ）‎ A．1 B．2 C．3 D．4‎ 一、 棱锥 3. 棱长为a的正四面体的外接球和内切球的半径是多少？ ‎ ‎ ‎ 4. 正四棱锥的底面边长和各侧棱长都为，点都在同一球面上，求此球的体积．‎ 二、 补形法 1. ‎《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；若四棱锥为阳马, ⊥平面, ， 四棱锥的五个顶点都在球的球面上, 则球的表面积为 ． ‎ 2. 三棱锥中, ⊥面, , ，, 三棱锥的四个顶点都在球的球面上, 则球的体积为 ． ‎ 3. ‎《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥为鳖臑, ⊥面, ，, 三棱锥的四个顶点都在球的球面上, 则球的表面积为（ ） ‎ A． B． C． D．‎ 4. 表面积为的正四面体的各个顶点都在同一个球面上，则此球的体积为(　　)‎ A．π B．π C．π D．π 一、 练习 1. 三棱锥PABC中，PA⊥平面ABC且PA＝2，△ABC是边长为的等边三角形，则该三棱锥外接球的表面积为（ ）‎ A． B．4π C．8π D．20π 2. 若三棱锥SABC的所有的顶点都在球O的球面上，SA⊥平面ABC，SA＝AB＝2，AC＝4，∠BAC＝，则球O的表面积为________．‎ 3. 已知正四棱锥的顶点都在同一球面上，且该棱锥的高为4，底面边长为2，则该球的表面积为________．‎ 4. 已知A，B，C是球O的球面上三点，AB＝2，AC＝2，∠ABC＝60°，且三棱锥OABC的体积为，则球O的表面积为________．‎ 5. 已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（ ）‎ A．π B． C． D． 6. 已知三棱柱ABCA1B1C1的底面是边长为的正三角形，侧棱垂直于底面，且该三棱柱的外接球的表面积为12π，则该三棱柱的体积为________．‎ 7. 四面体ABCD中，若AB＝CD＝，AC＝BD＝，AD＝BC＝2，则四面体ABCD的外接球的体积是________．‎ 8. 已知表面积为4π的球有一内接四棱锥，四边形ABCD是边长为1的正方形，且SA⊥平面ABCD，则四棱锥SABCD的体积为________．‎ 9. 已知A，B是球O的球面上两点，∠AOB＝90°，C为该球面上的动点．若三棱锥O ABC体积的最大值为36，则球O的表面积为（ ）‎ A．36π B．64π C．144π D．256π 10. 在半球内有一个内接正方体，试求这个半球的体积与正方体的体积之比．‎ 简单几何体的外接球和内切球问题的基本解法（教师版）‎ 一、 长方体，正方体相关问题 1. 正方体的内切球：球与正方体的每个面都相切，切点为每个面的中心，显然球心为正方体的中心．设正方体的棱长为，球半径为．如图，截面图为正方形的内切圆，得；‎ ‎ 截面图 2. 与正方体各棱相切的球：球与正方体的各棱相切，切点为各棱的中点，如图作截面图，圆为正方形的外接圆，易得．‎ ‎ 截面图 3. 正方体的外接球：正方体的八个顶点都在球面上，如图，以对角面作截面图得，圆为矩形的外接圆，易得．‎ ‎ 截面图 4. 长方体一个顶点上的三条棱的长度分别为，且它的个顶点都在同一球面上，则这个球的表面积为（ ）‎ A． B． C． D．‎ 一、 棱柱 1. 设三棱柱的侧棱垂直于底面，所有棱长都为，顶点都在一个球面上，则该球的表面积为（ B ）‎ A． B． C． D．‎ ‎【解析】由题意知，该三棱柱为正三棱柱，且侧棱与底面边长相等，均为 a．‎ 2. 已知各顶点都在一个球面上的正四棱柱的高为2，这个球的表面积为6π，则这个正四棱柱的体积为(　B　)‎ A．1 B．2 C．3 D．4‎ ‎【解析】S表＝4πR2＝6π，所以R＝．设正四棱柱底面边长为x，则2＋1＝R2，所以x＝1．所以V正四棱柱＝2．故选B．‎ 一、 棱锥 3. 棱长为a的正四面体的外接球和内切球的半径是多少？ ‎ ‎ ‎ ‎【解析】如图所示，设点是内切球的球心，正四面体棱长为．‎ 由图形的对称性知，点也是外接球的球心．设内切球半径为，外接球半径为．‎ 正四面体．‎ 正四面体 ‎， ‎ 在中，，即，得，得．‎ 1. 正四棱锥的底面边长和各侧棱长都为，点都在同一球面上，求此球的体积．‎ ‎【解析】设正四棱锥的底面中心为，外接球的球心为，‎ 如图所示，由球的截面的性质，可得．‎ 又，∴球心必在所在的直线上．‎ ‎∴的外接圆就是外接球的一个轴截面圆，外接圆的半径就是外接球的半径．‎ 在中，由，得．‎ ‎∴是以为斜边的．‎ ‎∴是外接圆的半径，也是外接球的半径．故．‎ 一、 补形法 2. ‎《九章算术》中，将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马；若四棱锥为阳马, ⊥平面, ， 四棱锥的五个顶点都在球的球面上, 则球的表面积为 ． ‎ 3. 三棱锥中, ⊥面, , ，, 三棱锥的四个顶点都在球的球面上, 则球的体积为 ． ‎ 1. ‎《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．若三棱锥为鳖臑, ⊥面, ，, 三棱锥的四个顶点都在球的球面上, 则球的表面积为（ ） ‎ A． B． C． D．‎ 2. 表面积为的正四面体的各个顶点都在同一个球面上，则此球的体积为(　　)‎ A．π B．π C．π D．π 一、 练习 3. 三棱锥PABC中，PA⊥平面ABC且PA＝2，△ABC是边长为的等边三角形，则该三棱锥外接球的表面积为(　　)‎ A． B．4π C．8π D．20π ‎【解析】选C　由题意得，此三棱锥外接球即以△ABC为底面、以PA为高的正三棱柱的 外接球，因为△ABC的外接圆半径r＝××＝1，外接球球心到△ABC的外接圆圆心的距离d＝1，所以外接球的半径R＝＝，‎ 所以三棱锥外接球的表面积S＝4πR2＝8π．‎ 1. 若三棱锥SABC的所有的顶点都在球O的球面上，SA⊥平面ABC，SA＝AB＝2，AC＝4，∠BAC＝，则球O的表面积为________．‎ ‎【解析】由题意，得三棱锥SABC是长方体的一部分(如图所示)，‎ 所以球O是该长方体的外接球，其中SA＝AB＝2，AC＝4，设球的半径为R，则2R＝＝＝2，‎ 所以球O的表面积为4πR2＝20π．‎ 2. 已知正四棱锥的顶点都在同一球面上，且该棱锥的高为4，底面边长为2，则该球的表面积为________．‎ ‎【解析】如图，正四棱锥PABCD的外接球的球心O在它的高PO1上，设球的半径为R，因为底面边长为2，所以AC＝4．在Rt△AOO1中，R2＝(4－R)2＋22，所以R＝，所以球的表面积S＝4πR2＝25π．‎ 3. 已知A，B，C是球O的球面上三点，AB＝2，AC＝2，∠ABC＝60°，且三棱锥OABC的体积为，则球O的表面积为________．‎ ‎【解析】∵AB＝2，AC＝2，∠ABC＝60°，∴在△ABC中，由正弦定理，得＝，解得sin C＝，又0°

查看更多