高考数学冲刺专题—椭圆

高考数学冲刺专题—椭圆

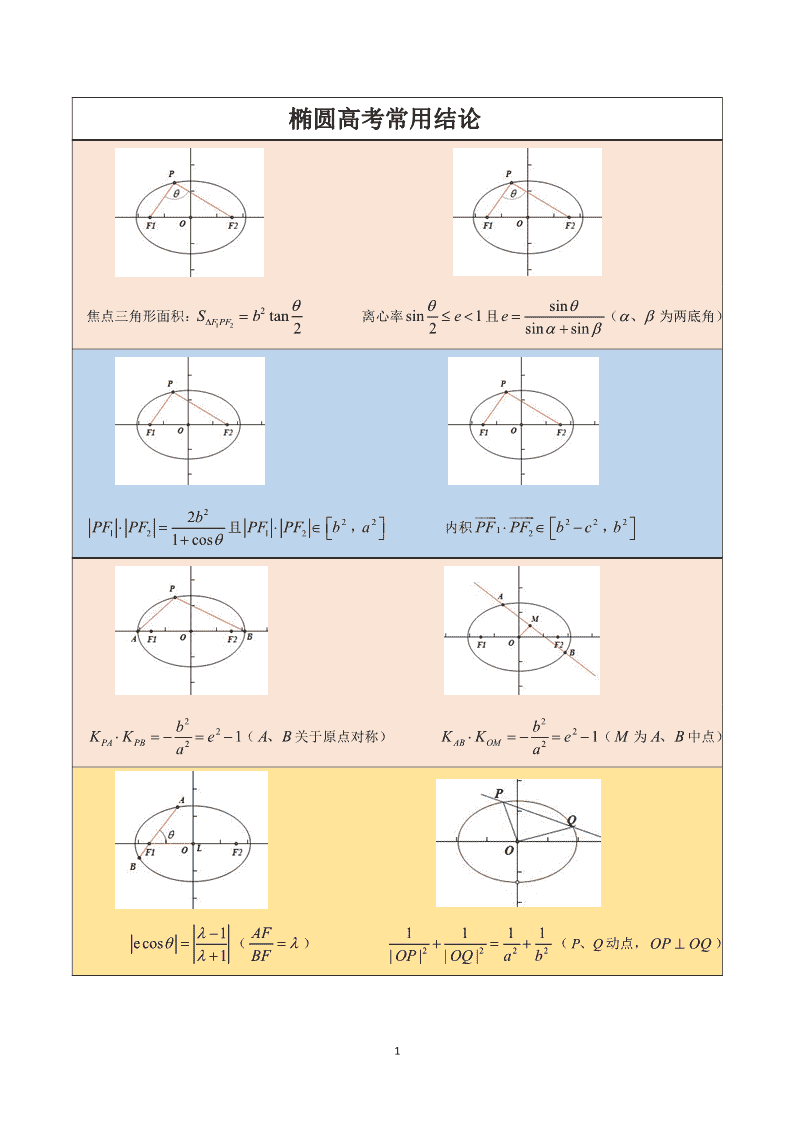
1 椭圆高考常用结论 焦点三角形面积： 1 2 2 tan 2F PFS b    离心率sin 12 e   且 sin sin sine     （ 、 为两底角） 2 1 2 2 1 cos bPF PF    且 2 2 1 2PF PF b a    ， 内积 2 2 2 1 2PF PF b c b       ， 2 2 2 1PA PB bK K ea      （ A B、 关于原点对称） 2 2 2 1AB OM bK K ea      （ M 为 A B、 中点） 1ecos 1     （ AF BF  ） 2 2 2 2 1 1 1 1 | | | |OP OQ a b    （ P Q、 动点，OP OQ ） 2 2020 高考专题—椭圆小题情缘 一、离心率情缘：生死之交 1．（2019•广州越秀月考）已知椭圆 2 2 2 2: 1( 0)x yE a ba b     右焦点为 (3,0)F 过点 F 的直线交 E 于 A ，B 两 点，若 AB 的中点坐标为 1(1, )2 ，则 E 的离心率是 ( ) A． 3 4 B． 13 4 C． 14 4 D． 15 4 【解答】点差法：设 1(A x ， 1)y ， 2(B x ， 2 )y ．可得： 2 2 1 1 2 2 1x y a b   ， 2 2 2 2 2 2 1x y a b   ．相减可得： 1 2 1 2 1 2 1 2 2 2 ( )( ) ( )( ) 0x x x x y y y y a b      ．又 1 2 2x x  ， 1 2 1y y  ， 1 2 1 2 1 0 12 1 3 4 y y x x      ． 2 2 2 1 04a b   ．  2 2 1 8 b a  ， 2 2 141 4 c be a a      ．故选 C ． 秒杀法：设 AB 的中点为 P ，直接结论 2 2 1 8OM AB bk k a      ， 2 2 141 4 c be a a      ． 2．（2019 春•沙市区校级期中）过原点 O 的直线 l 与椭圆 2 2 2 2: 1( 0)x yC a ba b     交于 M ， N 两点， P 是 椭圆 C 上异于 M ， N 的任一点．若直线 PM ， PN 的斜率之积为 1 3  ，则椭圆 C 的离心率为 ( ) A． 2 3 B． 6 3 C． 3 3 D． 1 2 【 解答 】设 0(P x ， 0 )y ， 1(M x ， 1)y ， 则 1(N x ， 1)y ，  2 2 0 0 2 2 1x y a b   ， 2 2 1 1 2 2 1x y a b   ． 相减 可 得： 2 2 2 2 1 0 1 0 2 2 0x x y y a b    ，即 2 2 2 1 0 2 2 2 1 0 y y b x x a    ． 线 PM ， PN 的斜率之积为 1 3  ， 1 0 1 0 1 0 1 0 1 3 y y y y x x x x      ， 2 2 1 3 b a    ，即 2 2 1 3 b a  ，椭圆 C 的离心率 2 2 61 3 c be a a     ．故选 B ． 秒杀法：设 AB 的中点为 P ，直接结论 2 2 1 3PM PN bk k a      ， 2 2 61 3 c be a a     ． 3 3．（2019•济南一模）设 1F ， 2F 分别是椭圆 2 2 2 2: 1( 0)x yE a ba b     的左、右焦点，过 2F 的直线交椭圆于 A ， B 两点，且 1 2 0AF AF    ， 2 22AF F B   ，则椭圆 E 的离心率为 ( ) A． 2 3 B． 3 4 C． 5 3 D． 7 4 【解答】设| | 3AB m ， 2 2| | 2 | |AF F B ， 2| | 2AF m  ， 2| |F B m ， 1| | 2 2AF a m   ， 1| | 2BF a m  ．  1 2 0AF AF    ， 1AB AF  ， 2 2 24 (2 ) (2 2 )c m a m    ， 2 2 2(2 ) (3 ) (2 2 )a m m a m    ，即 1 3m a ， 2 2 24 164 9 9c a a   ， 2 29 5c a  ， 5 3 c a  ．故选 C ． 4．（2019•拉萨二模）设椭圆 E 的两焦点分别为 1F ， 2F ，以 1F 为圆心， 1 2| |F F 为半径的圆与 E 交于 P ，Q 两点．若△ 1 2PF F 为直角三角形，则 E 的离心率为 ( ) A． 2 1 B． 5 1 2  C． 2 2 D． 2 1 【解答】如图所示，△ 1 2PF F 为直角三角形， 1 2 90PF F   ， 1| | 2PF c  ， 2| 2 2PF c ， 则 2 2 2 2c c a  ，解得 2 1ce a    ．故选 A ． 5．（2019 春•思明区校级月考）椭圆 2 2 2 2 1( 0)x y a ba b     的左、右焦点分别为 1F ， 2F ，点 P 在椭圆上，如 果 1PF 的中点在 y 轴上，且 1 2 5| | | |3PF PF ，则椭圆的离心率 e 为 ( ) A． 5 3 B． 2 2 C． 1 2 D． 5 3 【解答】 1PF 的中点在 y 轴上， Px c  ， 2 2| | bPF a   ， 2 1 2 5 5| | | |3 3 bPF PF a    ，又 2 25 23 b b aa a    ，化为： 2 24 3b a ．椭圆的离心率 2 2 3 11 1 4 2 c be a a       ．故选 C ． 4 6．（2019•贵州二模）过椭圆 2 2 2 2: 1( 0)x yC a ba b     的左焦点 F 的直线过 C 的上端点 B ，且与椭圆相交于 点 A ，若 3BF FA   ，则 C 的离心率为 ( ) A． 1 3 B． 3 3 C． 3 2 D． 2 2 【解答】解：由题意可得 (0, )B b ， ( ,0)F c ，由 3BF FA   可得 4( 3 cA  ， )3 b ，把点 A 在代入椭圆方程上， 得： 2 2 16 1 19 9 c a   ， 2 2 1 2 c a  ，故 2 2 ce a   ．故选 D ． 秒杀法：如图，焦比 1cos 1e     得 1 2 c c a a   ， 2 2 1 2 c a  ，故 2 2 ce a   ． 7 ． （ 2019 • 广 州 模 拟 ） 点 P 是 椭 圆 2 2 1 2 2: 1( 0)x yC a ba b     与 圆 2 2 2 2x y a b   的 一 个 交 点 ， 且 2 1 1 22 PF F PF F   ，其中 1F ， 2F 分别为椭圆 1C 的左、右焦点，则椭圆 1C 的离心率为 ( ) A． 3 1 B． 3 1 2  C． 2 1 D． 2 1 2  【解答】解：如图：因为椭圆 2 2 1 2 2: 1x yC a b   的焦点 2 2 1(F a b  ，0) ， 2 2 2 (F a b ，0) 而圆 2 2 2 2x y a b   的半径 2 2r a b  ，因此△ 1 2PF F 为直角三角形，又 2 1 1 22 PF F PF F   ，所以 1 2 60PF F  ， 2 1 30PF F   ， 1 2| | 2 2F F r c  ， 2| | 3PF c ， 1| |PF c ，由椭圆的定义可知 2 1| | | | 3 2PF PF c c a    ，椭圆的离心率 2 2 3 12 3 c ce a c c      ．故选 A ． 5 8．（2019•芜湖模拟）在直角坐标平面内，已知 ( 2,0)A  ， (2,0)B 以及动点 C 是 ABC 的三个顶点，且 sin sin 2cos 0A B C  ，则动点 C 的轨迹曲线  的离心率是 ( ) A． 2 2 B． 3 2 C． 2 D． 3 【解答】 sin sin 2cos 0A B C  ， sin sin 2cos 2cos( ) 2(cos cos sin sin )A B C A B A B A B        ， sin sin 2cos cosA B A B  ，即 tan tan 2A B  ， 2AC BCk k    ，设 ( , )C x y ，又 ( 2,0)A  ， (2,0)B ，所以有 2( 0)2 2 y y yx x      ，整理得 2 2 1, 04 8 x y y   ， 2 2a  ， 2c  ，离心率为： 2 2 c a  ，故选 A ． 秒杀法：特殊位置，点 C 在上顶点即可， 2 2 c a  ． 9．（2019•揭阳二模）设 F 是椭圆 2 2 2 2: 1( 0)x yE a ba b     的右焦点，A 是椭圆 E 的左顶点，P 为直线 3 2 ax  上一点， APF 是底角为 30 的等腰三角形，则椭圆 E 的离心率为 ( ) A． 3 4 B． 2 3 C． 1 2 D． 1 3 【解答】设 3 2 ax  交 x 轴于点 M ， FPA 是底角为 30 的等腰三角形 120PFA   ， | | | |PF FA ，且 | | 2 | |PF FM ， P 为直线 3 2 ax  上一点， 32( )2 a c a c    ，解之得 2 3a c 椭圆 E 的离心率为 2 3 ce a   故选 B ． 10．（2019•宜宾模拟）已知椭圆 2 2 2 2 1x y a b   的左右焦点分别为 1F ， 2F ，过 1F 作倾斜角为 45的直线与椭圆 交于 A ， B 两点，且 1 12F B AF   ，则椭圆的离心率 ( ) A． 3 3 B． 3 2 C． 2 2 D． 2 3 【解答】椭圆 2 2 2 2 1x y a b   的左右焦点分别为 1F ， 2F ，过 1( ,0)F c 且斜率为 1，为 1 的直线 y x c  ，交椭圆 于 A ， B ，代入椭圆方程，化简可得 2 2 2 2 2 2 2 2( ) 2 0a b y cb y c b a b     ，设 1(A x ， 1)y ， 2(B x ， 2 )y ，则 2 1 2 2 2 2cby y a b     ， 2 2 2 2 1 2 2 2 c b a by y a b   ，且 1 12F B AF   ，可得 2 12y y  ， 2 1 2 2 2cby a b     ， 2 2 2 2 2 1 2 22 c b a by a b    ， 可得， 2 2 2 2 2 2 2 2 2 2 22( )cb c b a b a b a b    ，可得 2 29 2c a ， 2 3 ce a   ．故选 D ． 6 另解：结论 1cos 1e     2 1 2 2 3 3e   . 11．（2019•吉安一模）如图，用与底面成 45角的平面截圆柱得一椭圆截线，则该椭圆的离心率为 ( ) A． 2 2 B． 3 3 C． 3 2 D． 1 3 【解答】设圆柱底面圆的方程为 2 2 2x y R  ，与底面成 45角的平面截圆柱，椭圆的半长轴长是 2R ， 半短轴长是 R ， c R  ， 2 22 c Re a R     ．故选 A ． 12．（2019•海淀区校级一模）已知 1F ， 2F 分别是椭圆 2 2 : 14 x yC m   的上下两个焦点，若椭圆上存在四个 不同点 P ，使△ 1 2PF F 的面积为 3 ，则椭圆 C 的离心率的取值范围是 ( ) A． 1(2 ， 3)2 B． 1(2 ，1) C． 3( 2 ，1) D． 3( 3 ，1) 【解答】 1F ， 2F 分别是椭圆 2 2 : 14 x yC m   的上下两个焦点，可得 2 2 4c m  ，短半轴的长： m ， 椭圆上存在四个不同点 P ，使得△ 1 2PF F 的面积为 3 ，可得 1 22  4 3m m   ，可得 2 4 3 0m m   ， 解得 (1,3)m ，则椭圆 C 的离心率为： 4 1(2 2 me   ， 3)2 ．故选 A ． 13．（2019•肇庆二模）已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的左右顶点分别为 A ，B ，P 是椭圆上异于 A ，B 的一点，若直线 PA 的斜率 PAk 与直线 PB 的斜率 PBk 乘积 1 4PA PBk k   ，则椭圆 C 的离心率为 ( ) A． 1 4 B． 1 2 C． 3 4 D． 3 2 【解答】设 0(P x ， 0 )y 代入椭圆方程，则 2 2 0 0 2 2: 1( 0)x yC a ba b     ，整理得： 2 2 2 2 0 02 ( )by x aa   ， 又 0 1 0 yk x a   ， 0 2 0 yk x a   ，所以 2 0 1 2 2 2 0 1 4 yk k x a    ，联立两个方程则 2 1 2 2 1 4 bk k a     ，即 2 2 1 4 b a  ，则 2 2 2 2 31 2 c be a a     ．故选 D ． 另解：结论 2 1 2 2 1 4 bk k a     . 7 14．（2018 秋•吉安期末） 1F ， 2F 是椭圆的两个焦点， P 是椭圆上异于顶点的一点，且△ 1 2F PF 是等腰直角 三角形，则椭圆的离心率为 ( ) A． 2 2 B． 1 2 2   C．1 2 2  D． 1 2  【解答】由△ 1 2PF F 是等腰直角三角形，且 P 是椭圆上异于顶点的一点，角 1F 或角 2F 为直角，不妨令角 2F 为直角，此时 ( , )P c y ，代入椭圆方程 2 2 2 2 1x y a b   （不妨设焦点在 x 轴上），解得 2by a   ，又三角形 1 2PF F 为等腰直角三角形，得 2 1 2PF F F ，故得 2 2b ca  ，即 2 22ac a c  ，即 2 2 1 0e e   ，解得 1 2e    ， 由 0 1e  ，可得 1 2e    ，故选 D ． 15．（2018 秋•张家口期末）已知椭圆 C 的中心在原点，焦点 1F ， 2F 在坐标轴上，点 P 为椭圆 C 上一点， 且 1| |PF ， 1 2| |F F ， 2| |PF 成等差数列，则椭圆 C 的离心率为 ( ) A． 2 2 B． 1 2 C． 2 4 D． 1 4 【解答】解： 1| |PF ， 1 2| |F F ， 2| |PF 成等差数列， 1 2 1 22 | | | | | | 2F F PF PF a    ，即 4 2c a ， 1 2 ce a    ， 故选 B ． 16．（2019•呼和浩特二模）已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的左、右顶点分别为 1A ， 2A ，点 P 是椭圆上 的动点，若 1 2A PA 的最大可以取到120 ，则椭圆 C 的离心率为 ( ) A． 1 2 B． 2 2 C． 3 2 D． 6 3 【解答】椭圆 2 2 2 2: 1( 0)x yC a ba b     的左、右顶点分别为 1A ， 2A ，点 P 是椭圆上的动点，若 1 2A PA 的最 大可以取到120 ，可知 P 在椭圆的短轴端点，所以 tan 60 3a b    ，所以 2 2 23( )a a c  ，所以 6 3 ce a   ， 故选 D ． 17．（2019•潍坊模拟）已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的左右焦点为 1F ， 2F ，若椭圆 C 上恰好有 6 个不 同的点，使得△ 1 2F F P 为等腰三角形， C 的离心率的取值范围是 ( ) A． 1 2( , )3 3 B． 1( ,1)2 C． 2( ,1)3 D． 1 1 1( , ) ( ,1)3 2 2 8 【解答】①当点 P 与短轴的顶点重合时，△ 1 2F F P 构成以 1 2F F 为底边的等腰三角形， 此种情况有 2 个满足条件的等腰△ 1 2F F P ； ②当△ 1 2F F P 构成以 1 2F F 为一腰的等腰三角形时，以 2F P 作为等腰三角形的底边为例， 1 2 1F F F P ，  点 P 在以 1F 为圆心，半径为焦距 2c 的圆上因此，当以 1F 为圆心，半径为 2c 的圆与椭圆 C 有 2 交点时， 存在 2 个满足条件的等腰△ 1 2F F P ，在△ 1 2 1F F P 中， 1 2 1 2F F PF PF  ，即 2 2 2 2c c a c   ， 由此得知 3c a ．所以离心率 1 3e  ．当 1 2e  时，△ 1 2F F P 是等边三角形，与①中的三角形重复，故 1 2e  同理，当 1F P 为等腰三角形的底边时，在 1 3e  且 1 2e  时也存在 2 个满足条件的等腰△ 1 2F F P 这样，总共有 6 个不同的点 P 使得△ 1 2F F P 为等腰三角形． 综上所述，离心率的取值范围是： 1(3e ， 1 1) (2 2  ，1) ，故选 D ． 18．（2018 春•沙坪坝区校级月考）如图所示，椭圆 2 2 2 2 1x y a b   中心在坐标原点，F 为左焦点，当 0FB AB    ， 其离心率为 5 1 2  ，此类椭圆被称为“黄金椭圆”．类比黄金椭圆，可推算出黄金双曲线的离心率等于 ( ) A． 5 1 2  B． 5 1 2  C． 5 1 D． 5 1 【解答】在 Rt ABF 中，由 AB BF 可得 2 2 2FB AB FA  ，则 2b ac ，即 2 2c a ac  ，可得 2 1e e  ， 又由 1e  ，则 5 1 2e  故选 B ． 9 19．（2019 春•安徽期末）椭圆 2 2 2 2: 1( 0)x yC a ba b     的左焦点为 F ，若 F 关于直线 0x y  的对称点 A 是椭园 C 上的点，则椭圆的离心率为 ( ) A． 2 2 B． 3 2 C． 2 1 D． 3 1 【解答】点 ( ,0)F c 关于直线 0x y  的对称点 A 为 (0, )A c ，且 A 在椭圆上，即 2 2b c ， c b  ，  椭圆 C 的离心率 2 2 2 2 2 2 2 c ce a b c    ．故选 A ． 20．（2019 春•雅安期末）椭圆 2 2 2 2 1( 0)x y a ba b     的左右焦点分别是 1F 、 2F ，以 2F 为圆心的圆过椭圆的 中心，且与椭圆交于点 P ，若直线 1PF 恰好与圆 2F 相切于点 P ，则椭圆的离心率为 ( ) A． 3 1 B． 3 1 2  C． 2 2 D． 5 1 2  【解答】椭圆 2 2 2 2 1( 0)x y a ba b     的左右焦点分别是 1F 、 2F ，以 2F 为圆心的圆过椭圆的中心，且与椭圆交 于点 P ，若直线 1PF 恰好与圆 2F 相切于点 P ，可得 2 2 2(2 ) 4a c c c   ，可得 2 22 2a ac c  ， 所以 2 2 2 0e e   ， (0,1)e ，解得 2 12 3 12e     ．故选 A ． 21．（2019 春•广州模拟）已知 1F 、 2F 分别是椭圆 2 2 2 2 1( 0)x y a ba b     的左、右焦点，椭圆上存在点 P 使 1 2F PF 为钝角，则椭圆的离心率的取值范围是    A． 2 12       ， B． 1 12      ， C． 20 2       ， D． 10 2      ， 【解答】解：设 0(P x ， 0 )y ，则 0| |x a ，又 1( ,0)F c ， 2 ( ,0)F c ，又 1 2F PF 为钝角，当且仅当 1 2 0PF PF    有 解，即 0( c x  ， 0 0) (y c x   ， 2 0 0 0 0) ( )( ) 0y c x c x y       ，即有 2 2 2 0 0c x y  有解，即 2 2 2 0 0( )minc x y  ． 又 2 2 2 2 0 02 by b xa   ， 2 2 2 2 2 2 0 0 02 [cx y b x ba      ， 2 )a ，即 2 2 2 0 0( )minx y b  ．故 2 2c b ， 2 2 2c a c  ，  2 2 1 2 c a  ，即 2 2e  ，又 0 1e  ， 2 12 e  ．故选 A ． 另解：结论 sin 2e  （ 为 1 2F PF ）， 2 12 e  . 另解： P 为上顶点. 10 二、直线斜率情缘：患难之交 1．（2019 春•汕尾期末）已知椭圆 2 2 : 18 6 x yC   的左、右顶点分别为 A 、 B ，点 P 为椭圆 C 上不同于 A 、 B 两点的动点，若直线 PA 斜率的取值范围是[1， 2]，则直线 PB 斜率的取值范围是 ( ) A．[ 2 ， 1] B． 3[ 2  ， 3]4  C．[ 1 ， 1]2  D． 3[ 4  ， 3]8  【解答】设椭圆 2 2 2 2 1( 0)x y a ba b     的左右顶点分别为 ( ,0)A a ， ( ,0)B a ， 0(P x ， 0 )y 为椭圆上不同于 A ， B 的任意一点，则 0 0 PA yk x a   ， 0 0 PB yk x a   ， 2 0 2 2 0 PA PB yk k x a    ，由 P 在椭圆上，得 2 2 0 0 2 2 1x y a b   ， 则 2 2 0 2 2 2 0 y b x a a   ．由椭圆 2 2 : 18 6 x yC   ，得 6 3 8 4PA PBk k     ， [1PAk  ，2]， 3 3[4 4PB PA k k     ， 3]8  ． 故选 D ． 秒杀法：直接结论 2 2 6 3 8 4PA PB bk k a       . 2．（2019 春•沙市区校级期中）过原点 O 的直线 l 与椭圆 2 2 2 2: 1( 0)x yC a ba b     交于 M ， N 两点， P 是 椭圆 C 上异于 M ， N 的任一点．若直线 PM ， PN 的斜率之积为 1 3  ，则椭圆 C 的离心率为 ( ) A． 2 3 B． 6 3 C． 3 3 D． 1 2 【解答】设 0(P x ， 0 )y ， 1(M x ， 1)y ，则 1(N x ， 1)y ， 2 2 0 0 2 2 1x y a b   ， 2 2 1 1 2 2 1x y a b   ． 相减可得： 2 2 2 2 1 0 1 0 2 2 0x x y y a b    ，即 2 2 2 1 0 2 2 2 1 0 y y b x x a    ．线 PM ， PN 的斜率之积为 1 3  ，  1 0 1 0 1 0 1 0 1 3 y y y y x x x x      ， 2 2 1 3 b a    ，即 2 2 1 3 b a  ，椭圆 C 的离心率 2 2 61 3 c be a a     ，故选 B ． 秒杀法：直接结论 2 2 1 3PM PN bk k a      . 3．（2019•唐山三模）设椭圆 2 2 2 2: 1( 0)x yC a ba b     的左，右焦点分别为 1F ， 2F ，离心率为 5 3 ，以 1 2F F 为直径的圆与 C 在第一象限的交点为 P ，则直线 1PF 的斜率为 ( ) A． 1 3 B． 1 2 C． 3 3 D． 3 2 【解答】 5 3 c a  ， 3 5 a c  ， 2 2 2 29 2 5 5 b a c c c c     ，设 1| |PF m ， 2| |PF n ， ( )m n ． 11 则 62 5 m n a c   ， 2 2 24m n c  ，化为： 2 25 6 5 8 0m cm c   ，解得 2 5 5n c ， 4 5 5m c ． 直线 1PF 的斜率 1 2 n m   ．故选 B ． 4．（2019•肇庆二模）已知椭圆 2 2 2 2: 1( 0)x yC a ba b     的左右顶点分别为 A ，B ，P 是椭圆上异于 A ，B 的一点，若直线 PA 的斜率 PAk 与直线 PB 的斜率 PBk 乘积 1 4PA PBk k   ，则椭圆 C 的离心率为 ( ) A． 1 4 B． 1 2 C． 3 4 D． 3 2 【解答】设 0(P x ， 0 )y 代入椭圆方程，则 2 2 0 0 2 2: 1( 0)x yC a ba b     ，整理得： 2 2 2 2 0 02 ( )by x aa   ， 又 0 1 0 yk x a   ， 0 2 0 yk x a   ，所以 2 0 1 2 2 2 0 1 4 yk k x a    ，联立两个方程则 2 1 2 2 1 4 bk k a     ，即 2 2 1 4 b a  ， 则 2 2 2 2 31 2 c be a a     ．故选 D ． 秒杀法：直接结论法 2 2 1 4PA PB bk k a      ． 5．（2018 秋•天河区校级月考）已知椭圆 2 2 2 2: 1( 0)x y a ba b      的长轴是短轴的 2 倍，过右焦点 F 且斜率 为 ( 0)k k  的直线与  相交于 A ， B 两点．若 3AF FB   ，则 (k  ) A．1 B．2 C． 3 D． 2 【解答】椭圆 2 2 2 2: 1( 0)x y a ba b      的长轴是短轴的 2 倍，解得 2a b ， 3c b ，设过右焦点 F 且斜率 为 ( 0)k k  的直线与椭圆 C 相交于 A ， B 两点， 1(A x ， 1)y ， 2(B x ， 2 )y ， 3AF FB   ， 1 23y y   ， 设直线 AB 方程为 ( 3 )y k x b  ，代入 2 2 2 4 x y b  ，消去 x ，可得 2 2 2 2(1 4 ) 2 3 0k y kby k b    ， 1 2 2 2 3 1 4 kby y k      ， 2 2 1 2 21 4 k by y k    ， 2 2 2 32 1 4 kby k     ， 2 2 2 2 23 1 4 k by k     ，解得 2k  ．故选 D ． 秒杀法：焦比公式 1cos 1e     ，由题意得 3 2e  ， 3  ，解得 3cos 3   ，即 tan 2k   . 12 6．（2018 秋•湖州期中）椭圆 2 2 : 19 8 x yC   的左、右顶点分别为 1A ， 2A ，点 P 在 C 上且直线 2PA 斜率的取 值范围是[ 2 ， 1] ，那么直线 1PA 斜率的取值范围是 ( ) A． 1 8[ , ]2 9 B． 4 8[ , ]9 9 C． 1[ ,1]2 D． 8[ ,1]9 【解答】由椭圆的标准方程可知，左右顶点分别为 1( 3,0)A  、 2 (3,0)A ，设点 (P m ， )( 3)n m   ， 则 2 2 19 8 m n  ①， 1 3PA nk m   ， 2 3PA nk m   ；则 1 2 2 23 3 9PA PA n n nk k m m m       ． 将①式代入得 1 2 9 8PA PAk k   ． 2 [ 2PAk   ， 1] ， 1 4 8[ , ]9 9PAk  ．故选 B ． 秒杀法：结论 1 2 2 2 9 8PA PA bk k a      ， 2 [ 2PAk   ， 1] ， 1 4 8[ , ]9 9PAk  7．（2018 秋•三明期中）已知椭圆 2 2: 14 xM y  ，直线 1 与椭圆 M 交于 A 、B 两点，且点 1(1, )2D 是弦 AB 的中点，则直线 1 的方程为 ( ) A． 4 3 0x y   B． 4 1 0x y   C． 2 2 0x y   D． 2 0x y  【解答】当直线 l 的斜率不存在时不符合题意．设直线 l 的斜率为 k ．设点 1(A x ， 1)y ， 2(B x ， 2 )y ． 代入椭圆方程得 2 21 1 14 x y  ， 2 22 2 14 x y  ．两式相减得 1 2 1 2 1 2 1 2 ( )( ) ( )( ) 04 x x x x y y y y      ， 点 1(1, )2D 为弦 AB 的中点， 1 2 2x x   ， 1 2 1y y  ．又 1 2 1 2 y y kx x   ， 解得 1 2k   ．  直线 l 的方程为 1 1 ( 1)2 2y x    ，化为 2 2 0x y   ．故选 C ． 秒杀法：结论 2 2 1 4OD AB bk k a      ，因为 1 2ODk  ，所以 1 2ABk   ． 13 三、向量情缘：忘年之交 1．（2019•福田区校级模拟）在平面直角坐标系 xOy 中，已知点 A ，F 分别为椭圆 2 2 2 2: 1( 0)x yC a ba b     的右顶点和右焦点，过坐标原点 O 的直线交椭圆 C 于 P ，Q 两点，线段 AP 的中点为 M ，若 Q ，F ，M 三 点共线，则椭圆 C 的离心率为 ( ) A． 1 3 B． 2 3 C． 8 3 D． 3 2 或 8 3 【解答】设 0(P x ， 0 )y ，则 0(Q x ， 0 )y ， 0( 0)y  ． ( ,0)A a ， ( ,0)F c ，则 0 0( , )2 2 x a yM  ． Q ， F ， M 三点共线， QF MFk k  ， 0 0 00 2 2 y y x ax c c      ，化为： 3a c ， 1 3e  ，故选 A ． 2．（2019 春•邕宁区校级期中）若点 O 和 F 分别为椭圆 2 2 14 x y  的中心和左焦点，点 P 为椭圆上的任意 一点，则 OP FP   的最小值为 ( ) A． 4 2 3 B．0 C．1 D． 4 2 3 【解答】由题意， ( 3F  ， 0) ，设点 0(P x ， 0 )y ，则有 2 20 0 14 x y  ，解得 2 2 0 0 1 4 xy   ，  0( 3FP x   ， 0 )y ， 0(OP x  ， 0 )y ， 2 2 20 0 0 0 0 0 0 0 3( 3) ( 3) (1 ) 3 14 4 xOP FP x x y x x x x             ， 此二次函数对应的抛物线的对称轴为 2 3 3x   ， 02 2x „ „ ，当 0 2 3 3x   时，则 OP FP   的最小值为 0． 故选 B ． 3．（2019•济南一模）设 1F ， 2F 分别是椭圆 2 2 2 2: 1( 0)x yE a ba b     的左、右焦点，过 2F 的直线交椭圆于 A ， B 两点，且 1 2 0AF AF    ， 2 22AF F B   ，则椭圆 E 的离心率为 ( ) A． 2 3 B． 3 4 C． 5 3 D． 7 4 【解答】设| | 3AB m ， 2 2| | 2 | |AF F B ， 2| | 2AF m  ， 2| |F B m ， 1| | 2 2AF a m   ， 1| | 2BF a m  ．  1 2 0AF AF    ， 1AB AF  ， 2 2 24 (2 ) (2 2 )c m a m    ， 2 2 2(2 ) (3 ) (2 2 )a m m a m    ，即 1 3m a ， 2 2 24 164 9 9c a a   ， 2 29 5c a  ， 5 3 c a  ．故选 C ． 14 4．（2019 春•沙坪坝区校级月考）已知椭圆的左右焦点分别为 1( 1,0)F  ， 2 (1,0)F ， P 为椭圆上一点，且满 足 1 2 6PF PF    ，△ 1 2PF F 的面积为 3 3 ，则椭圆长轴长为 ( ) A．3 B．6 C． 10 D． 2 10 【解答】设 1| |PF m  ， 2| |PF n  ， 1 2F PF   ，由 1 2 6PF PF    ，得 cos 6mn   ， 又 1 2 1 sin 3 32F PFS mn    ．得 tan 3  ， 3   ，则 12mn  ．在△ 1 2PF F 中，由余弦定理可得： 2 2 22 2 cos 3m n mn    ，即 2 2 2 24 ( ) 3 ( ) 36m n mn m n mn m n         ， 2( ) 40m n   ，即 2 10m n  ．椭圆长轴长为 2 10 ．故选 D ． 秒杀法： 1 2 2 tan 3 32PF F pS b c y      ，所以 3 3 2Py  ，又 1 2 6PF PF    ，解得 1 3 3 2 2P       ， ，代入椭圆方程 得 10a  . 5．（2019•贵州二模）过椭圆 2 2 2 2: 1( 0)x yC a ba b     的左焦点 F 的直线过 C 的上端点 B ，且与椭圆相交于 点 A ，若 3BF FA   ，则 C 的离心率为 ( ) A． 1 3 B． 3 3 C． 3 2 D． 2 2 【解答】由题意可得 (0, )B b ， ( ,0)F c ，由 3BF FA   可得 4( 3 cA  ， )3 b ，把点 A 在代入椭圆方程上，得： 2 2 16 1 19 9 c a   ， 2 2 1 2 c a  ，故 2 2 ce a   ．故选 D ． 秒杀法：如图，焦比 1cos 1e     得 1 2 c c a a   ， 2 2 1 2 c a  ，故 2 2 ce a   ． 15 6．（2019•宜宾模拟）已知椭圆 2 2 2 2 1x y a b   的左右焦点分别为 1F ， 2F ，过 1F 作倾斜角为 45 的直线与椭圆 交于 A ， B 两点，且 1 12F B AF   ，则椭圆的离心率 ( ) A． 3 3 B． 3 2 C． 2 2 D． 2 3 【解答】椭圆 2 2 2 2 1x y a b   的左右焦点分别为 1F ， 2F ，过 1( ,0)F c 且斜率为 1，为 1 的直线 y x c  ，交椭圆 于 A ， B ，代入椭圆方程，化简可得 2 2 2 2 2 2 2 2( ) 2 0a b y cb y c b a b     ，设 1(A x ， 1)y ， 2(B x ， 2 )y ，则 2 1 2 2 2 2cby y a b     ， 2 2 2 2 1 2 2 2 c b a by y a b   ，且 1 12F B AF   ，可得 2 12y y  ， 2 1 2 2 2cby a b     ， 2 2 2 2 2 1 2 22 c b a by a b    ， 可得， 2 2 2 2 2 2 2 2 2 2 22( )cb c b a b a b a b    ，可得 2 29 2c a ， 2 3 ce a   ．故选 D ． 秒杀法： 1cos 1e     2 1 2 2 3 3e e     ． 7．（2019•桂林模拟）已知 A ，B ，C 为椭圆 2 2 12 x y  上三个不同的点，O 为坐标原点，若 0OA OB OC       ， 则 ABC 的面积为 ( ) A． 3 3 8 B． 6 3 C． 3 6 4 D． 3 6 2 【解答】设直线 :AB y kx m  ，代入 2 22 2x y  得 2 2 2(1 2 ) 4 2( 1) 0k x kmx m     设 1(A x ， 1)y ， 2(B x ， 2 )y ，则 1 2 2 4 1 2 kmx x k     ， 2 1 2 2 2( 1) 1 2 mx x k   ，设 3(C x ， 3 )y ，由 0OA OB OC       ， 则 3 1 2 2 4( ) 1 2 kmx x x k      ， 2 3 1 2 1 2 2 2 4 2( ) [ ( ) 2 ] ( 2 )1 2 1 2 k m my y y k x x m mk k               ， 代 入 2 22 2x y  得 2 21 2 4k m  ， 2 1 2| | 1 | |AB k x x   ， O 到直线 AB 的距离为 2 | | 1 md k   ， 由三角形的重心性质可得  22 2 2 2 2 2 2 1 21 1 4 4 1 22 2 1 2 1 2 1 2OAB m mkmS d AB m k mk k k                2 2 634 4 m mm    ，可得 3 63 4ABC OABS S   ．故选 C ． 16 8．（2018 秋•天河区校级月考）已知椭圆 2 2 2 2: 1( 0)x y a ba b      的长轴是短轴的 2 倍，过右焦点 F 且斜率 为 ( 0)k k  的直线与  相交于 A ， B 两点．若 3AF FB   ，则 (k  ) A．1 B．2 C． 3 D． 2 【解答】椭圆 2 2 2 2: 1( 0)x y a ba b      的长轴是短轴的 2 倍，解得 2a b ， 3c b ，设过右焦点 F 且斜率 为 ( 0)k k  的直线与椭圆 C 相交于 A ， B 两点， 1(A x ， 1)y ， 2(B x ， 2 )y ， 3AF FB   ， 1 23y y   ， 设直线 AB 方程为 ( 3 )y k x b  ，代入 2 2 2 4 x y b  ，消去 x ，可得 2 2 2 2(1 4 ) 2 3 0k y kby k b    ， 1 2 2 2 3 1 4 kby y k      ， 2 2 1 2 21 4 k by y k    ， 2 2 2 32 1 4 kby k     ， 2 2 2 2 23 1 4 k by k     ，解得 2k  ．故选： D ． 秒杀法：焦比公式 1cos 1e     ，由题意得 3 2e  ， 3  ，解得 3cos 3   ，即 tan 2k   . 9．（2019 春•惠州校级月考）已知椭圆 2 2 : 116 12 x yC   左右焦点分别为 1F ， 2F ， P 为椭圆上的动点，求 1 2PF PF   的最小值 . 【解答】设点  4cos 2 3sinP  ， ，由题意得    1 22 0 2 0F F  ， ， ， ，则  1 2 4cos 2 3sinPF       ， ，  2 2 4cos 2 3sinPF      ， ，  2 2 2 2 2 1 2 4 16cos 12sin 16cos 12sin 4cos 8PF PF                ，当且 仅当 2cos 0  ，即 90  时等号成立，所以 1 2PF PF   的最小值为 8. 秒杀法：由 2 2 21 2PF PF b c b       ， 得最小值为12 4 8  . 10．（2019•凉山州模拟）设 1F ， 2F 是椭圆 2 2 : 125 16 x yE   的左右焦点， P 是椭圆 E 上的点，则 1 2| | | |PF PF 的最小值是 ． 【解答】由椭圆 2 2 : 125 16 x yE   ，得 2 25a  ， 2 16b  ，则 5a  ， 25 16 3c    ， P 是椭圆 E 上的 点 1 2| | | | 2 10PF PF a    ，且 25 3 2 | | 5 3 8PF      ， 2 1 2 2 2 2 2| | | | (10 | |) | | | | 10| |PF PF PF PF PF PF        ， 当 2| | 2PF  或 8 时， 1 2| | | |PF PF 的最小值是 16．故答案为 16． 秒杀法：由 2 2 1 2PF PF b a    ， 得最小值为 16. 17 四、三角形面积情缘：点头之交 1．（2019•郑州一模）椭圆 2 2 125 16 x y  的焦点为 1F ， 2F ， P 为椭圆上一点，若 1 2 60F PF  ，则△ 1 2F PF 的 面积是 ( ) A．16 3 3 B． 32 3 3 C．16 3 D．32 3 【解答】由椭圆 2 2 125 16 x y  ，得 5a  ， 4b  ， 3c  ，在△ 1 2F PF 中， 1 2 60F PF   ，由余弦定理可得： 2 2 2 1 2 1 2 1 2| | | | | | 2| || | cos60F F PF PF PF PF    ，则 2 2 1 24 (2 ) 3| || |c a PF PF  ，即 1 236 100 3| || |PF PF  ， 1 2 64| || | 3PF PF  ．△ 1 2F PF 的面积是 1 2 1 16 3| || | sin602 3S PF PF   ．故选 A ． 秒杀法：结论 1 2 2 16 3tan 2 3PF FS b     . 2．（2018 秋•浉河区校级月考）已知椭圆 2 2 2 2 1( 0)x y a ba b     的左顶点、上顶点和左焦点分别为 A ， B ， F ，中心为 O ，其离心率为 1 2 ，则 : (ABF BFOS S   ) A．1:1 B．1: 2 C． (2 3) : 2 D． 3 : 2 【解答】如图， 1 2 ce a   ， 2a c  ， 2AF a c c c c      ，则 1 2ABFS bc  ， 1 2BFOS bc  ， : 1:1ABF BFOS S   ．故选 A ． 3．（2019•桂林模拟）已知 A ，B ，C 为椭圆 2 2 12 x y  上三个不同的点，O 为坐标原点，若 0OA OB OC       ， 则 ABC 的面积为 ( ) A． 3 3 8 B． 6 3 C． 3 6 4 D． 3 6 2 【解答】设直线 :AB y kx m  ，代入 2 22 2x y  得 2 2 2(1 2 ) 4 2( 1) 0k x kmx m     设 1(A x ， 1)y ， 2(B x ， 2 )y ，则 1 2 2 4 1 2 kmx x k     ， 2 1 2 2 2( 1) 1 2 mx x k   ，设 3(C x ， 3 )y ，由 0OA OB OC       ， 则 3 1 2 2 4( ) 1 2 kmx x x k      ， 2 3 1 2 1 2 2 2 4 2( ) [ ( ) 2 ] ( 2 )1 2 1 2 k m my y y k x x m mk k               ， 18 代入 2 22 2x y  得 2 21 2 4k m  ， 2 1 2| | 1 | |AB k x x   ， O 到直线 AB 的距离为 2 | | 1 md k   ， 由三角形的重心性质可得  22 2 2 2 2 2 2 1 21 1 4 4 1 22 2 1 2 1 2 1 2OAB m mkmS d AB m k mk k k                2 2 634 4 m mm    ，可得 3 63 4ABC OABS S   ．故选 C ． 4．（2018 秋•大港区期中）已知椭圆 2 2 15 4 x y  的两个焦点为 1F ， 2F ，点 P 在椭圆上，△ 1 2PF F 是直角三 角形，则△ 1 2PF F 的面积为 ( ) A． 8 5 5 B． 8 5 5 或 4 C． 4 5 5 D． 4 5 5 或 4 【解答】由椭圆 2 2 15 4 x y  可得： 2 5a  ， 2 4b  ， 2 2 2 1c a b    ． ①若 1PF x 轴，或 2PF x 轴时，把 1x   代入椭圆方程得 21 15 4 y  ，解得 4 5 5y   ， 4 5 5h  ，  △ 1 2PF F 的面积 1 2 1 1 4 5 4 5| | 22 2 5 5F F h      ． ②若 P 为椭圆短轴的一个顶点 (0,2) ，在 1Rt POF 中， 1 1tan 12OPF   ， 1 45OPF   ， 1 2 90F PF   ， 故不可能有 1 2PF PF 故选 C ． 5．（2018 秋•河南期中）如图所示， 1A ， 2A 是椭圆 2 2 : 118 9 x yC   的短轴端点，点 M 在椭圆上运动，且点 M 不与 1A ， 2A 重合，点 N 满足 1 1NA MA ， 2 2NA MA ，则 1 2 1 2 (MA A NA A S S  ) A．2 B．3 C．4 D． 5 2 【解答】由题意以及选项的值可知： 1 2 1 2 MA A NA A S S 是常数，所以取 M 为椭圆的左顶点，由椭圆的性质可知 N 在 x 的正半轴上，如图：则 1(0,3)A ， 2A 是 (0, 3) ， ( 3 2M  ，0) ， 2 1OM ON OA  ，可得 3 3 2 22 ON   ， 则 1 2 1 2 2 1 2 1 1 2 21 2 MA A NA A A A MOS MO S NOA A NO    ．故选 A ． 19 四、求值（最值）情缘：泛泛之交 1．（2019 春•福清市校级期中）已知椭圆 2 2 2: 1( 2)4 y xC aa    的离心率 3 ,3 P 为椭圆 C 上的一个动点，则 P 与定点 ( 1,0)B  连线距离的最大值为 ( ) A． 3 2 B． 5 2 C． 30 2 D．3 【解答】由题意可得： 3 3 c a  ， 2b  ， 2 2 2a b c  ，联立解得 6a  ， 2b  ， 椭圆的标准方程为： 2 2 16 4 y x  ．设 (2sin , 6 cos )P   ， [0  ， 2 ) ． 则 2 2 2 2 2 2| | (2sin 1) ( 6 cos ) 2cos 4sin 5 2sin 4sin 7 2(sin 1) 9 9PB                      ． 当 sin 1  时取等号． | | 3PB  ，选 D ． 另解：此题数据太差，秒选 D ． 2．（2019•新课标Ⅰ）已知椭圆 C 的焦点为 1( 1,0)F  ， 2 (1,0)F ，过 2F 的直线与 C 交于 A ， B 两点．若 2 2| | 2 | |AF F B ， 1| | | |AB BF ，则 C 的方程为 ( ) A． 2 2 12 x y  B． 2 2 13 2 x y  C． 2 2 14 3 x y  D． 2 2 15 4 x y  【解答】 2 2| | 2 | |AF BF ， 2| | 3| |AB BF  ，又 1| | | |AB BF ， 1 2| | 3| |BF BF  ，又 1 2| | | | 2BF BF a  ， 2| | 2 aBF  ， 2| |AF a  ， 1 3| | 2BF a ，在 Rt △ 2AF O 中， 2 1cos AF O a   ，在△ 1 2BF F 中，由余弦定理可得 2 2 2 1 34 ( ) ( )2 2cos 2 2 2 a a BF F a       ，根据 2 2 1cos cos 0AF O BF F    ，可得 21 4 2 02 a a a   ，解得 2 3a  ， 3a  ． 2 2 2 3 1 2b a c     ．所以椭圆 C 的方程为： 2 2 13 2 x y  ．故选 B ． 秒杀法：设 2F B x ，则 2 2F A x ， 1 2 1 2 2F A F A F B F B a    ，所以 1 2AF x ，由焦比公式 1cos 1e     ， 得 1 3 c c a a   ，所以 2 1 3e  ，故选 B ． 20 3．（2019•博望区校级模拟）已知椭圆 2 2 2: 1xC ya   的左，右焦点分别为 1F ， 2F ， A ， B 分别为椭圆 C 与 x ， y 正半轴的交点，直线 AB 与以 1 2F F 为直径端点的圆相切， 2a 的值为 ( ) A．1 5 2  B． 3 5 2  C．1 5 D．3 5 【解答】直线 AB 的方程为： 1| | x ya   ，即 | | | | 0x a y a   ，直线 AB 与以 1 2F F 为直径端点的圆相切，  2 2 | | 1 1 a c a a     ，解得 2 1 5 2a  ，故选 A ． 4．（2019 春•漳州期中）已知 AB 是椭圆 2 2 125 5 x y  的长轴，若把线段 AB 五等份，过每个分点作 AB 的垂 线，分别与椭圆的上半部分相交于 C ，D ，E ，G 四点，设 F 是椭圆的左焦点，则| | | | | | | |FC FD FE FG   的值是 ( ) A．15 B．16 C．18 D．20 【解答】椭圆 2 2 125 5 x y  的 5a  ， 5b  ， 2 5c  ， 2 5 5 ce a   ，左准线方程为 25 2 5 x   ， 由题意可得 3Cx   ， 1Dx   ， 1Ex  ， 3Gx  ，由椭圆的第二定义可得 | | 2 5 25 5 2 5C FC x   ， 可得 2 5| | 5 5 CFC x  ，同理可得 2 5| | 5 5 DFD x  ， 2 5| | 5 5 EFE x  ， 2 5| | 5 5 GFG x  ， 可得 2 5| | | | | | | | 20 ( 3 1 1 3) 205FC FD FE FG          ．故选： D ． 5．（2019 春•宝山区校级月考）已知点 P 为椭圆 2 2 19 16 x y  上的任意一点，点 1F ， 2F 分别为该椭圆的上下 焦点，设 1 2PF F   ， 2 1PF F   ，则 sin sin  的最大值为 ( ) A． 3 7 7 B． 4 7 7 C． 9 8 D． 3 2 【解答】设 1| |PF m ， 2| |PF n ，在△ 1 2PF F 中，由正弦定理可得： 2 sin sin sin( ) n m c       ， 可得： 2 7 sin sin sin( ) m n        ， 2 8m n a   ． 4sin sin sin( ) 7        ，当且仅当 P 为短轴的一个 21 端点时， ( )    取得最大角，  ，满足 3sin 4   ． sin( )   的最大值可为 1． 4 4 4 7sin sin sin( ) 77 7       „ ．故选 B ． 6．（2019•河南模拟）设 1F ， 2F 是椭圆 2 2 : 13 x yC m   的两个焦点，若 C 上存在点 P 满足 1 2 120F PF   ， 则 m 的取值范围是 ( ) A． (0 ，1] [12 ， ) B． 3(0, ] [2 3, )2  C． 3(0, ] [2 3, )4  D． 3(0, ] [12, )4  【解答】假设椭圆 2 2 : 13 x yC m   的焦点在 x 轴上，则 0 3m  ，假设 M 位于短轴的端点时， 1 2F MF 取最 大 值 ， 要 使 椭 圆 C 上 存 在 点 M 满 足 1 2 120F MF   ， 1 2 120F MF … ， 1 60F MO … ， 1 3tan tan60 3c mF MO b m     … ，解得： 30 4m „ ；当椭圆的焦点在 y 轴上时， 3 m ， 假设 M 位于短轴的端点时， 1 2F MF 取最大值，要使椭圆 C 上存在点 M 满足 1 2 120F MF   ， 1 2 120F MF … ， 1 60F MO … ， 1 3tan tan60 3 3 mF MO    … ，解得：12 m„ ， m 的取值范围是 (0 ， 3] [124  ， ) 故选 D ． 22 7．（2019 春•沙坪坝区校级月考）已知椭圆的左右焦点分别为 1( 1,0)F  ， 2 (1,0)F ， P 为椭圆上一点，且满 足 1 2 6PF PF    ，△ 1 2PF F 的面积为 3 3 ，则椭圆长轴长为 ( ) A．3 B．6 C． 10 D． 2 10 【解答】设 1| |PF m  ， 2| |PF n  ， 1 2F PF   ，由 1 2 6PF PF    ，得 cos 6m n    ， 又 1 2 1 sin 3 32F PFS m n      ．得 tan 3  ， 3   ，则 12m n  ．在△ 1 2PF F 中，由余弦定理可得： 2 2 22 2 cos 3m n mn    ， 即 2 2 2 24 ( ) 3 ( ) 36m n mn m n mn m n         ， 2( ) 40m n   ， 即 2 10m n  ．椭圆长轴长为 2 10 ．故选 D ． 8．（2019 春•洛阳期末）已知点 A ， B 是曲线 2 24 1x y  上两点，且 (OA OB O 为坐标原点），则 2 2 1 1 (| | | |OA OB   ) A． 3 4 B．1 C． 5 4 D．5 【解答】（1）若 OA 斜率为 0，则| | 1OA  ， 1| | 2OB  ， 2 2 1 1 5| | | |OA OB   ， （2）若 OA 有斜率且不为 0，设直线 OA 的方程为 y kx ，则直线 OB 的方程为 1y xk   ， 联立方程组 2 24 1 y kx x y     ，解得 2 2 1 1 4x k   ，故 2 2 21 4 ky k   ， 2 2 2 2 2 1| | 1 4 kOA x y k      ，将 1 k  替换 k 可得： 222 2 2 11 1| | 4 41 kkOB k k     ， 2 2 2 2 2 2 1 1 1 4 4 5| | | | 1 1 k k OA OB k k       ．综上， 2 2 1 1 5| | | |OA OB   ，故选 D ． 秒杀法：直接结论 2 2 2 2 1 1 1 1 | | | |OP OQ a b    ，得 2 2 1 1 5| | | |OA OB   . 9．（2019•宣城二模）已知双曲线 2 2 1( 0, 0)x y m nm n     和椭圆 2 2 15 2 x y  有相同的焦点，则 4 1 m n  的最 小值为 ( ) A．2 B．3 C．4 D．5 【解答】椭圆 2 2 15 2 x y  的焦点 ( 3 ，0) ，双曲线 2 2 1( 0, 0)x y m nm n     和椭圆 2 2 15 2 x y  有相同的焦点， 所以 3m n  ，则 4 1 1 4 1 1 4 1 4( )( ) (5 ) (5 2 ) 33 3 3 n m n mm nm n m n m n m n         … ．当且仅当 2 2m n  时， 23 取等号．故选 B ． 10．（2018 秋•和平区校级期末）已知椭圆 2 2 125 16 x y  的左右焦点分别为 1F 、 2F ，点 P 在椭圆上，若 P 、 1F 、 2F 是一个直角三角形的三个顶点，则点 p 到 x 轴的距离为 ( ) A． 9 5 B．4 C． 9 7 5 D．16 5 【解答】设椭圆短轴的一个端点为 M ．由于 5a  ， 4b  ， 3c b   ； 1 2 90F MF   ，  只能 1 2 90PF F   或 2 1 90PF F   ．令 3x   ，得 2 16 5 by a   ，故选 D ． 11．（2018 秋•房山区期末） F 是椭圆 2 2 125 16 x y  的右焦点，椭圆上至少有 21 个不同的点 ( 1iP i  ，2，3， ) ， 1| |PF ， 2| |P F ， 3| |P F ，组成公差为 ( 0)d d  的等差数列，则 d 的最大值为 ( ) A． 2 5 B． 3 10 C． 1 5 D． 1 10 【解答】由椭圆 2 2 125 16 x y  ，得 5a  ， 4b  ，则 2 2 3c a b   ．由已知可得等差数列是增数列， 则 1 1| | 5 3 2a FP   … ， 21 21| | 5 3 8a FP   „ ， 21 1 20a a d   ， 21 10 20 6a a d    „ ，解得 30 10d „ ． d 的最大值为 3 10 ．故选 B ． 12．（2018 秋•三明期中）已知椭圆 2 2: 14 xM y  ，直线 1 与椭圆 M 交于 A 、B 两点，且点 1(1, )2D 是弦 AB 的中点，则直线 1 的方程为 ( ) A． 4 3 0x y   B． 4 1 0x y   C． 2 2 0x y   D． 2 0x y  【解答】当直线 l 的斜率不存在时不符合题意．设直线 l 的斜率为 k ．设点 1(A x ， 1)y ， 2(B x ， 2 )y ． 代入椭圆方程得 2 21 1 14 x y  ， 2 22 2 14 x y  ．两式相减得 1 2 1 2 1 2 1 2 ( )( ) ( )( ) 04 x x x x y y y y      ， 点 1(1, )2D 为弦 AB 的中点， 1 2 2x x   ， 1 2 1y y  ．又 1 2 1 2 y y kx x   ， 解得 1 2k   ．  直线 l 的方程为 1 1 ( 1)2 2y x    ，化为 2 2 0x y   ．故选 C ． 秒杀法：直接结论 2 2 1 4OD AB bk k a      ，又因为 1 2ODk  ，所以 1 2ABk   ，直线方程为 2 2 0x y   ． 24 13．（2019 春•宾阳县校级月考）已知 F 是椭圆 2 2: 12 xC y  的左焦点， P 为 C 上一点， 1( 1, )2A  ，则 | | | |PA PF 的最大值为 ( ) A．3 2 B． 17 2 22  C．5 2 17 D．10 【解答】 F 是椭圆 2 2: 12 xC y  的左焦点，如图，设椭圆的右焦点为 F ，则| | | | 2 2PF PF   ； (1,0)F ， 由图形知，当 P 在直线 AF 上时，| | | |PA PF 取得最大值． 2 21 17| | ( 1 1) ( 0)2 2AF        ． 17| | | | 2 2 | | | | 2 2 2PA PF PF PF     „ ， | | | |PA PF  的最大值为 172 2 2  ，故选 B ． 14．（2019 春•玉山县校级期中）设 1F ， 2F 是椭圆 2 2 16 4 x y  的两个焦点，点 M 在椭圆上，若线段 1MF 的 中点在 y 轴上，则 2 1 | | | | MF MF 的值为 ( ) A． 1 5 B． 3 4 C． 2 3 D． 1 2 【解答】 1F ， 2F 是椭圆 2 2 16 4 x y  的两个焦点，可得 1( 2F  ， 0) ， 2 ( 2F ， 0) ． 2a  ， 1b  ． 点 M 在椭圆上，若线段 1MF 的中点在 y 轴上， 1 1 2MF F F ， 2 2 2 6| | 3 bMF a   ，由勾股定理可得： 1 2 6 4 6| | 2 6 3 3MF    ． 2 1 2 6 | | 13 | | 24 6 3 MF MF   ．故选 D ． 25 六、共焦点情缘：金石之交 2 2 2 2 1 2 sin cos2 2 1e e     （ 1 2e e、 分别为椭圆、双曲线离心率， 为 1 2F PF ） 1．（209 秋•黄山期末）已知 1F ， 2F 是椭圆和双曲线的公共焦点，点 P 是它们的一个公共点，且 1 2 60F PF  ， 设椭圆和双曲线的离心率分别为 1e 、 2e ，则 1 2 1 1 e e  的最大值为 ( ) A． 3 4 B． 4 3 C． 3 3 4 D． 4 3 3 【解答】设椭圆方程是 2 2 2 2 1 1 1x y a b   ，双曲线方程是 2 2 2 2 2 2 1x y a b   ，由定义可得 1 2 1| | | | 2PF PF a  ， 1 2 2| | | | 2PF PF a  ， 1 1 2| |PF a a   ， 2 1 2| |PF a a  ，在△ 1 2F PF 中由余弦定理可得， 2 2 2 1 2 1 2 1 2 1 2(2 ) ( ) ( ) 2( )( )cos60c a a a a a a a a        ，即 2 2 2 1 24 3c a a  ， 2 2 1 2 1 34 e e    ， 由柯西不等式得 2 2 2 2 1 2 1 2 1 2 1 1 3 1 1 3 1 1(1 )( ) (1 ) ( )3 3e e e e e e       … ，即 2 1 2 1 1 4 16( ) 43 3e e   „ ， 即 1 2 1 1 4 3 3e e  „ ，当且仅当 1 3 3e  ， 2 3e  时取等号．故选 D ． 秒杀法：由结论 2 2 1 2 1 34 e e    ，设 1 2 1 32cos 2sine e   ， ，得   1 2 1 1 2 3 4 32cos sin sin3 3e e         ， 所以 1 2 max 1 1 e e       4 3 3 ． 2．（2018•杭州月考）设点 P 为有公共焦点 1F 、 2F 的椭圆 M 和双曲线  的一个交点，且 1 2 3cos 5F PF  ， 椭圆 M 的离心率为 1e ，双曲线  的离心率为 2e ．若 2 12e e ，则 1 (e  ) A． 7 5 B． 7 4 C． 10 5 D． 10 4 【 解 答 】 如 图 ， 设 椭 圆 与 双 曲 线 的 标 准 方 程 分 别 为 ： 2 2 2 2 1 1 1x y a b   ， 2 2 2 2 2 2 1( i x y aa b   ， 0ib  ， 1 1a b ， 1i  ， 2) ， 2 2 2 2 2 1 1 2 2a b a b c    ， 0c  ． 设 1| |PF m ， 2| |PF n ．则 12m n a  ， 22n m a  ，解 得 1 2m a a  ， 1 2n a a  ， 由 1 2 3cos 5F PF  ， 在 △ 1 2PF F 中 ， 由 余 弦 定 理 可 得 ： 2 2 2 3(2 ) 2 5c m n mn   ， 2 2 2 1 2 1 2 1 2 1 2 64 ( ) ( ) ( )( )5c a a a a a a a a        ，化 26 为 2 2 2 1 25 4c a a  ， 2 2 1 2 1 4 5e e   ． 2 12e e ， 1 10 5e  ，故选 C ． 秒杀法：由 1 2 3cos 5F PF  ，得 2 21 2 1 21 cos 1 cos1 4sin cos2 2 5 2 2 5 F PF F PF       ， ，所以 2 2 1 2 1 4 5 e e   所以 1 10 5e  . 3．（2019 春•韶关利哥数学）已知椭圆C 和双曲线 E 有共同的焦点 1F 、 2F ，点 P 为它们的一个交点，且 1 2 3F PF   ，若椭圆 C 和双曲线 E 的离心率分别为 1 2e e、 ，当 1 2 1 e e 取得最大值时， 1 2e e、 的值分别是 ( ) A． 2 2 2 6、 B． 1 2 2 5、 C． 2 2 2 6、 D． 2 34 、 【解答】不妨设椭圆与双曲线的标准方程分别为： 2 2 2 2 1( 0)x y a ba b     ， 2 2c a b  ， 2 2 2 2 1 1 1x y a b   2 2 1 1c a b  ．设 1| |PF m ， 2| |PF n ． m n ．则 2m n a  ， 12m n a  ， 1m a a   ， 1n a a  ． 2 2 2(2 ) 1cos 3 2 2 m n c mn     ，化为： 2 2 2 1 1 1 1( ) ( ) 4 ( )( )a a a a c a a a a       ． 2 2 2 13 4 0a a c   ，  2 2 1 2 1 3 4e e   ， 2 2 1 2 1 34 2 e e    ，化为： 1 2 1 2 3e e  ，当且仅当 1 2 2e  ， 2 6 2e  时取等号．故选 A ． 秒杀法： 1 2 2 2 1 2 1 360 4F PF e e      ，所以 4  2 2 2 2 1 2 1 2 1 2 1 3 1 3 2 32e e e e e e     ，所以 1 2 1 2 3 3e e  ，当且仅当 2 2 2 2 1 2 1 2 1 3 1 3 4e e e e   ， ，即 1 2 2 6 2 2e e ， 时等号成立．