- 2021-07-01 发布 |
- 37.5 KB |
- 15页


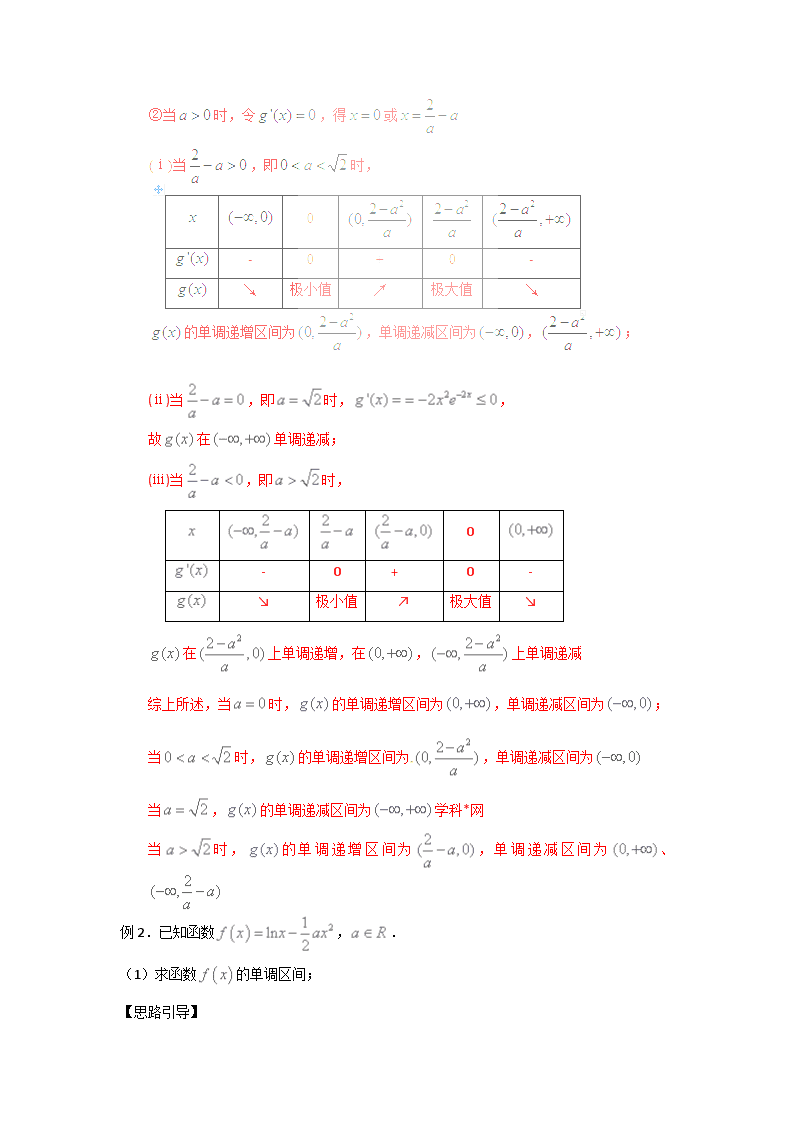
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018届二轮复习导数定调情况多,参数分类与整合学案(全国通用)
【题型综述】 用导数研究函数的单调性 (1)用导数证明函数的单调性 证明函数单调递增(减),只需证明在函数的定义域内()0 (2)用导数求函数的单调区间 求函数的定义域→求导→解不等式>0得解集→求,得函数的单调递增(减)区间. 一般地,函数在某个区间可导,>0在这个区间是增函数 一般地,函数在某个区间可导,<0在这个区间是减函数 (3)单调性的应用(已知函数单调性) 一般地,函数在某个区间可导,在这个区间是增(减)函数≥ 1、利用导数求函数f(x)的单调区间的一般步骤: (1)确定函数f(x)的定义域;(2)求导数f′(x); (3)在函数f(x)的定义域内解不等式f′(x)>0和f′(x)<0; (4)根据(3)的结果确定函数f(x)的单调区间. 2、求函数的单调区间的“两个”方法 方法一:(1)确定函数y=f(x)的定义域;(2)求导数y′=f′(x); (3)解不等式f′(x)>0,解集在定义域内的部分为单调递增区间;[来源:学科网] (4)解不等式f′(x)<0,解集在定义域内的部分为单调递减区间. 方法二:(1)确定函数y=f(x)的定义域; (2)求导数y′=f′(x),令f′(x)=0,解此方程,求出在定义区间内的一切实根; (3)把函数f(x)的间断点(即f(x)的无定义点)的横坐标和上面的各实数根按由小到大的顺序排列起来,然后用这些点把函数f(x)的定义区间分成若干个小区间; (4)确定f′(x)在各个区间内的符号,根据符号判定函数在每个相应区间内的单调性. 3、由函数的单调性求参数的取值范围的方法 (1)可导函数在某一区间上单调,实际上就是在该区间上(或)( 在该区间的任意子区间内都不恒等于0)恒成立,然后分离参数,转化为求函数的最值问题,从而获得参数的取值范围; (2)可导函数在某一区间上存在单调区间,实际上就是(或)在该区间上存在解集,这样就把函数的单调性问题转化成了不等式问题; (3)若已知在区间I上的单调性,区间I中含有参数时,可先求出的单调区间,令I是其单调区间的子集,从而可求出参数的取值范围. 【典例指引】 例1.已知函数,为函数的导函数. (1)设函数的图象与x轴交点为A,曲线y=f(x)在A点处的切线方程是,求的值; (2)若函数,求函数的单调区间. (Ⅱ). ①当时,, 学科*网 0 - 0 + ↘ 极小值 ↗ 的单调递增区间为,单调递减区间为 (ⅱ)当,即时,, 故在单调递减; (ⅲ)当,即时, 0 - 0 +[来源:学*科*网] 0 - ↘ 极小值 ↗ 极大值 ↘ 在上单调递增,在,上单调递减 综上所述,当时,的单调递增区间为,单调递减区间为; 当时,的单调递增区间为,单调递减区间为 当,的单调递减区间为学科*网 当时,的单调递增区间为,单调递减区间为、 例2.已知函数,. (1)求函数的单调区间; 【思路引导】 (1)先确定函数的定义域,求导后得,根据正负进行讨论,可得函数的单调区间; 试题解析:(1)函数的定义域为. 由题意得, 当时, ,则在区间内单调递增; 当时,由,得或(舍去), 当时,,单调递增, 当时,,单调递减. 所以当时, 的单调递增区间为,无单调递减区间; 当时, 的单调递增区间为,单调递减区间为.学科*网 例3.已知函数, ,(其中, 为自然对数的底数, ……). (1)令,求的单调区间; 【思路引导】 (1)求导函数的导数得,再根据是否变号进行分类讨论单调性:当时,导函数不变号,为单调递增;当时,导函数先负后正,对应单调区间为先减后增. 所以的减区间为 ,增区间为 综上可得,当时, 在上单调递增 当时, 的增区间为,减区间为.学科*网 例4.已知函数其中实数为常数且. (I)求函数的单调区间; 【思路引导】 (1)利用导数并结合实数的不同取值求解单调区间; 例5.已知函数. (1)讨论的单调性; 【思路引导】 (1)求出,分类讨论,分别由可得增区间,由可得减区间 【同步训练】 1.已知 (1)若 ,且函数 在区间 上单调递增,求实数a的范围; 【思路引导】 (1)求导后根据函数在区间单调递增,导函数大于或等于0(2)先判断为一个零点,然后再求导,根据,化简求得另一个零点。 解析:(1)当时,,因为函数在上单调递增,所以当时,恒成立.学科*网 函数的对称轴为. ①,即时,,即,解之得,解集为空集; ②,即时, 即,解之得,所以 ③,即时, 即,解之得,所以 综上所述,当 函数在区间 上单调递增.学科*网 2.已知函数. (1)讨论的单调性; 【思路引导】 (1)对函数进行求导分解因式可得 ,分为和讨论导数与0的关系,得到单调性; 3.设函数 (1)讨论的单调性; 【思路引导】 (1)函数f(x)的定义域为(0,+∞),,对m分类讨论即可得出. 试题解析:(1)函数定义域为, 当时, ,∴在上单调递增; 当时, 得, ∴在上单调递增;在上单调递减. 点评:讨论函数的单调性即讨论导函数的正负,导函数中有参数m,需要对m进行讨论,来判断正负; 4.已知函数 ,其中 (为自然对数的底数). (Ⅰ)讨论函数的单调性,并写出相应的单调区间; 【思路引导】 (I)求出,对和分别讨论单调性,求出单调区间; 5.已知函数, . (1)求函数的单调区间; 【思路引导】 (1)先确定函数的定义域,求导后得,根据正负进行讨论,可得函数的单调区间; 6.已知函数,其中为自然对数的底数.[来源:学+科+网Z+X+X+K] (1)讨论函数在区间上的单调性; 【思路引导】 (1)求出,讨论三种情况, , ,分别令可得增区间, 可得减区间; 试题解析:(1),①当时,,,在上单调递增,②当时,,,在上单调递增,③当时, 时,,在上单调递增,时,,在上单调递减,④当时,,,在上单调递增,综上所述,当或时, 在上单调递增,当时,在上单调递增,在上单调递减 7.设函数. (1)讨论函数的单调性;[来源:学#科#网] (2)若,求函数的最值. 【思路引导】 (1)先求导,分类讨论即可求出函数的单调区间;(2)求导,根据导数和函数的最值得关系即可求出,注意分类讨论. ④若,则恒成立,所以函数在上单调递减. (2)若, ①当时, ,由(1)得,函数在上单调递增,在上单调递减, 故时,函数有最大值,无最小值; ②当时, ,由(1)得,函数在上单调递增,在上单调递减, 故时,函数有最小值,无最大值. 8.已知函数f(x)=ln (x+1)- -x,a∈R. (1)当a>0时,求函数f(x)的单调区间; 【思路引导】 (1)先求导数,转化研究二次函数符号变化规律:当判别式非正时,导函数不变号;当判别式大于零时,定义域上有两个根 ,导函数符号先负再正再负. 9.已知常数,函数. (1)讨论在区间上的单调性; 【思路引导】 (1)结合函数的解析式可得,分类讨论有: 当时,在区间上单调递增; 当时,在区间上单调递减,在区间上单调递增; 试题解析:(1) 当时,此时,在区间上单调递增 当时,,得 当时,;时,; 故在区间上单调递减,在区间上单调递增 综上所述,当时,在区间上单调递增;当时,在区间上单调递减,在区间上单调递增 点评:导数是研究函数的单调性、极值(最值)最有效的工具,而函数是高中数学中重要的知识点,所以在历届高考中,对导数的应用的考查都非常突出. 10.已知函数. (1)若,求曲线在点处的切线方程; (2)求函数的单调区间; (3)设函数.若对于任意,都有成立,求实数的取值范围. 【思路引导】 (1)代入,求导,可求出切线方程。(2)因为.又因为,的两根>0,所以分与与三类讨论单调性。(3)由成立,即,变形.,所以只需。查看更多