高考数学复习课时提能演练(四十二) 7_1

高考数学复习课时提能演练(四十二) 7_1

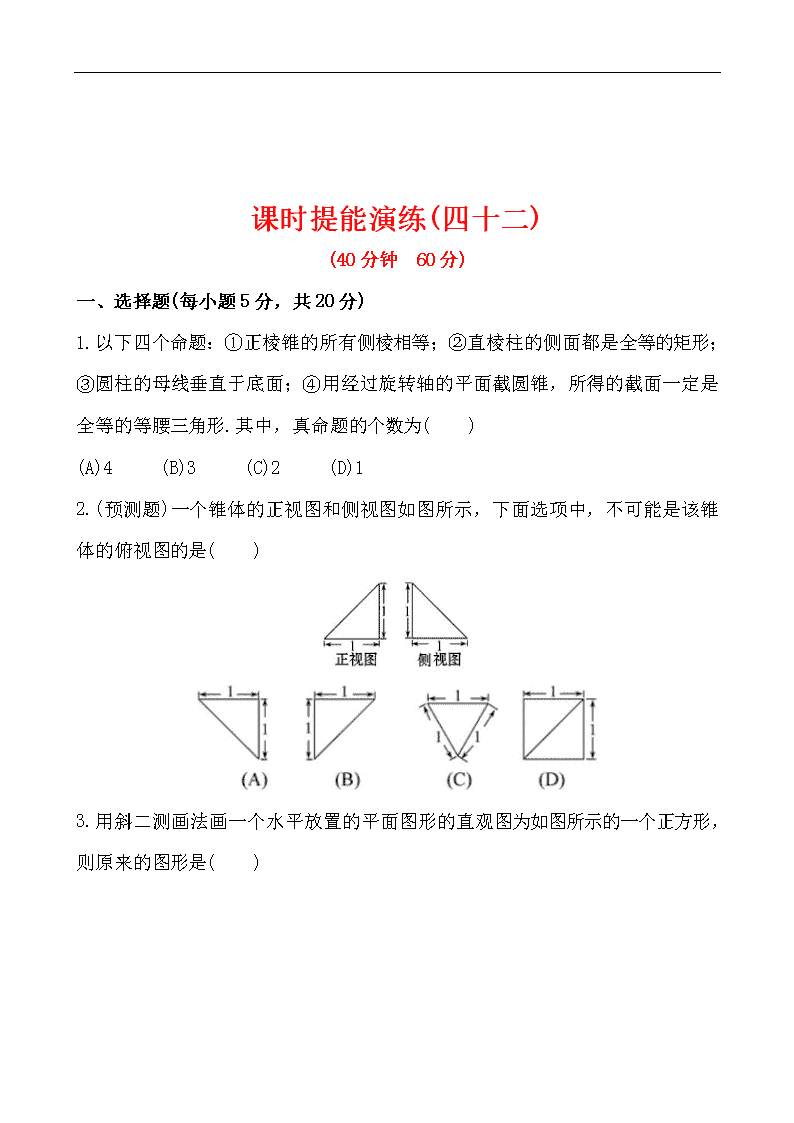
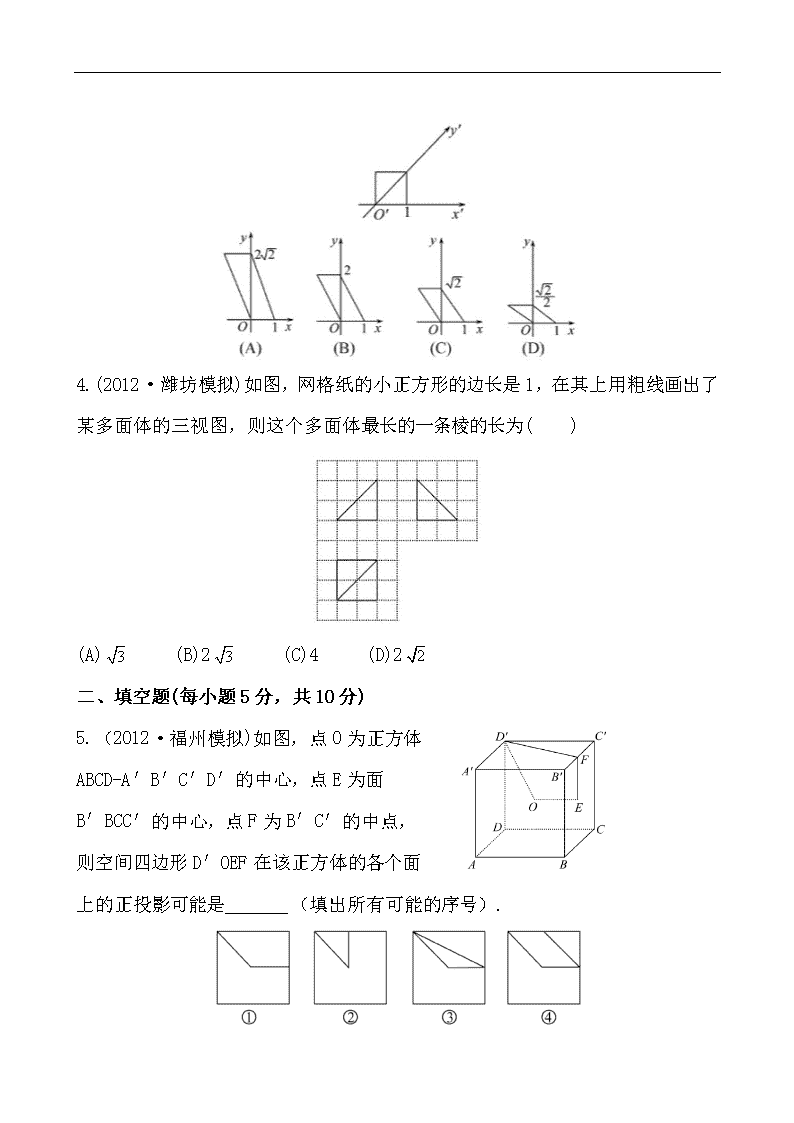
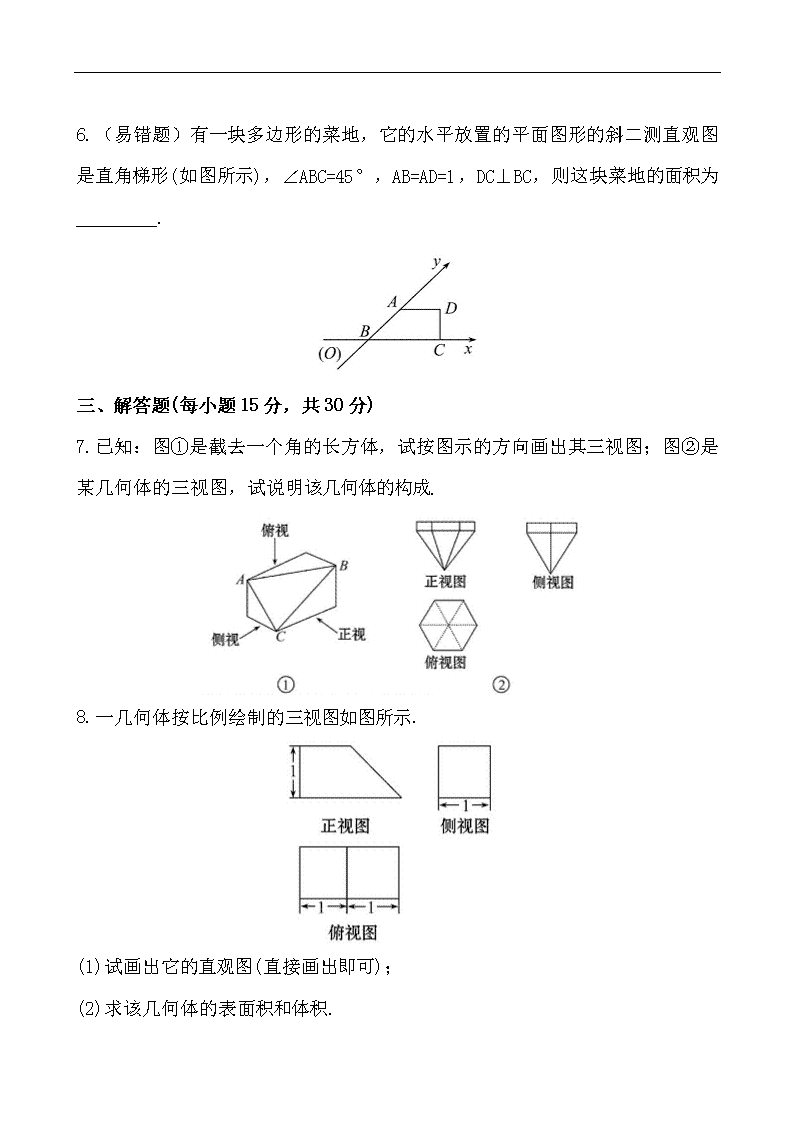
‎ ‎ 课时提能演练(四十二)‎ ‎(40分钟 60分)‎ 一、选择题(每小题5分，共20分) ‎ ‎1.以下四个命题：①正棱锥的所有侧棱相等；②直棱柱的侧面都是全等的矩形；③圆柱的母线垂直于底面；④用经过旋转轴的平面截圆锥，所得的截面一定是全等的等腰三角形.其中，真命题的个数为( )‎ ‎(A)4 (B)3 (C)2 (D)1‎ ‎2.(预测题)一个锥体的正视图和侧视图如图所示，下面选项中，不可能是该锥体的俯视图的是( )‎ ‎3.用斜二测画法画一个水平放置的平面图形的直观图为如图所示的一个正方形，则原来的图形是( )‎ ‎4.(2012·潍坊模拟)如图，网格纸的小正方形的边长是1，在其上用粗线画出了某多面体的三视图，则这个多面体最长的一条棱的长为( )‎ ‎(A) (B)2 (C)4 (D)2‎ 二、填空题(每小题5分，共10分)‎ ‎5.（2012·福州模拟)如图，点O为正方体 ‎ ABCD-A′B′C′D′的中心，点E为面 B′BCC′的中心，点F为B′C′的中点，‎ 则空间四边形D′OEF在该正方体的各个面 上的正投影可能是_______（填出所有可能的序号）.‎ ‎6.（易错题）有一块多边形的菜地，它的水平放置的平面图形的斜二测直观图是直角梯形(如图所示)，∠ABC=45°，AB=AD=1，DC⊥BC，则这块菜地的面积为_________.‎ 三、解答题(每小题15分，共30分)‎ ‎7.已知：图①是截去一个角的长方体，试按图示的方向画出其三视图；图②是某几何体的三视图，试说明该几何体的构成.‎ ‎8.一几何体按比例绘制的三视图如图所示.‎ ‎(1)试画出它的直观图(直接画出即可)；‎ ‎(2)求该几何体的表面积和体积.‎ 答案解析 ‎1.【解析】选B.由正棱锥的定义可知所有侧棱相等，故①正确；由于直棱柱的底面不一定是正多边形，故侧面矩形不一定全等，因此②不正确；由圆柱母线的定义可知③正确；结合圆锥轴截面的作法可知④正确.‎ 综上，正确的命题有3个.‎ ‎2.【解析】选C.当俯视图为A、B时表示底面为等腰直角三角形，且过直角顶点的棱与底面垂直的三棱锥.当俯视图为D时，表示底面为正方形，且有一条侧棱与底面垂直的四棱锥.故选C.‎ ‎【方法技巧】由直观图画三视图的技巧 ‎(1)可以想象将一几何体放在自己面前,然后从正前方,左侧及上面观察该几何体,进而得到正视图、侧视图和俯视图.‎ ‎(2)在画三视图时,要注意看得见的轮廓线画成实线,看不见的轮廓线画成虚线.‎ ‎3.【解析】选A.由题意知直观图是边长为1的正方形，对角线长为，所以原图形为平行四边形,且位于y轴上的对角线长为2.‎ ‎4.【解析】选B.由三视图知，该几何体为四棱锥P-ABCD(如图)，其中底面ABCD是边长为2的正方形,‎ PC⊥平面ABCD,PC=2.故PB=PD=2,‎ ‎，所以最长棱的长为.‎ ‎5.【解析】①是空间四边形D′OEF在平面CDD′C′上的投影；②是空间四边形D′OEF在侧面BCC′B′上的投影；③是空间四边形D′OEF在平面 A′B′C′D′上的投影；④不是D′OEF在正方体面上的投影.‎ 答案：①②③‎ ‎6.【解析】在直观图中，过点A作AE⊥BC,垂足为E,‎ 则在Rt△ABE中，AB=1,∠ABE=45°，∴BE=.‎ 而四边形AECD为矩形，AD=1，‎ ‎∴EC=AD=1.‎ ‎∴BC=BE+EC=+1.‎ 由此可还原原图形如图.‎ 在原图形中，A′D′=1,A′B′=2,‎ B′C′=+1,且A′D′∥B′C′,A′B′⊥B′C′.‎ ‎∴这块菜地的面积为S=(A′D′+B′C′)·A′B′‎ ‎.‎ 答案：‎ ‎7.【解析】图①几何体的三视图为：‎ 图②所示的几何体是上面为正六棱柱，下面为倒立的正六棱锥的组合体.‎ ‎8.【解析】(1)直观图如图所示，‎ ‎(2)由三视图可知该几何体是长方体被截去一部分，且该几何体的体积是以A1B1,A1D1,A‎1A为长，宽，高的长方体体积的.‎ 在直角梯形AA1B1B中，‎ 作BE⊥A1B1于E，则AA1EB是正方形.‎ ‎∴AA1=EB=1.‎ 在Rt△BEB1中，EB=EB1=1，∴BB1=.‎ ‎∴几何体的表面积 ‎ =1+2××(1+2)×1+1×+1+1×2=7+.‎ 几何体的体积V=×1×2×1=.‎ 即所求几何体的表面积为7+，体积为.‎