2018届二轮复习1-2不等关系及简单不等式的解法课件(全国通用)
1
.
2
不等关系及简单不等式的解法
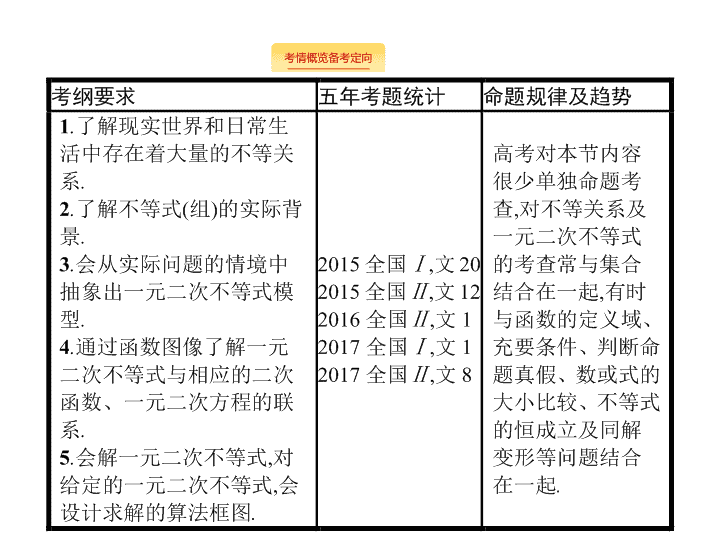
考情概览备考定向
必备知识预案自诊
3
知识梳理
考点自测
>
=
<
>
=
<
必备知识预案自诊
4
知识梳理
考点自测
2
.
不等式的性质
(1)
对称性
:
a>
b
⇔
b
b
,
b
>c
⇒
.
(3)
可加性
:
a>
b
⇔
a+c
b+c
;
a
>
b
,
c
>
d
⇒
a+c
b+d
.
(4)
可乘性
:
a>
b
,
c
>
0
⇒
ac
bc
;
a
>
b
,
c
<
0
⇒
ac
bc
;
a>b>
0,
c>d>
0
⇒
ac
bd.
(5)
可乘方
:
a>b>
0
⇒
a
n
b
n
(
n
∈
N
,
n
≥
1)
.
a>c
>
>
>
<
>
>
>
必备知识预案自诊
5
知识梳理
考点自测
3
.
三个
“
二次
”
之间的关系
{
x|x
>x
2
或
xb
⇔
ac
2
>bc
2
.
(
)
(3)
若关于
x
的不等式
ax
2
+bx+c<
0
的解集为
(
x
1
,
x
2
),
则必有
a>
0
.
(
)
(4)
不等式
的解集是
[
-
1,2]
.
(
)
(5)
若关于
x
的方程
ax
2
+bx+c=
0(
a
≠0)
没有实数根
,
则关于
x
的不等式
ax
2
+bx+c>
0
的解集为
R
.
(
)
×
√
√
×
×
必备知识预案自诊
9
知识梳理
考点自测
2
.
(2017
江西吉抚七校质量监测
2,
文
5)
若
0
b
3
B.
C.
a
b
>
1
D.lg(
b
-a
)
<
0
3
.
已知
a
,
b
>
0,
且
a
≠1,
b
≠1
.
若
log
a
b
>
1,
则
(
)
A.(
a-
1)(
b-
1)
<
0 B.(
a-
1)(
a-b
)
>
0
C.(
b-
1)(
b-a
)
<
0 D.(
b-
1)(
b-a
)
>
0
D
解析
:
∵
0
1,
得
b
0,(
a-
1)(
a-b
)
<
0,(
b-a
)(
b-
1)
>
0
.
∴
排除
A,B,C
.
当
a>
1
时
,
由
log
a
b
>
1,
得
b>a>
1
.
∴
b-a>
0,
b-
1
>
0
.
∴
(
b-
1)(
b-a
)
>
0
.
故选
D
.
必备知识预案自诊
10
知识梳理
考点自测
D
[
-
3,1]
关键能力学案突破
11
考点一
考点二
考点三
学科素养微专题
考点四
比较两个数
(
式
)
的大小
例
1
(1)
已知
a
1
,
a
2
∈
(0,1),
若
M=a
1
a
2
,
N=a
1
+a
2
-
1,
则
M
与
N
的大小关系是
(
)
A.
MN
C.
M=N
D.
不确定
(2)
若
,
则
(
)
A.
a
0,
即
M-N>
0
.
∴
M>N.
(2)(
方法一
)
由题意可知
a
,
b
,
c
都是正数
.
关键能力学案突破
13
考点一
考点二
考点三
学科素养微专题
考点四
思考
比较两个数
(
式
)
大小常用的方法有哪些
?
解题心得
比较大小常用的方法有作差法、作商法、构造函数法
.
(1)
作差法的一般步骤
:
①
作差
;
②
变形
;
③
定号
;
④
下结论
.
变形常采用配方、因式分解、有理化等方法把差式变成积式或者完全平方式
.
(2)
作商法一般适用于分式、指数式、对数式
,
作商只是思路
,
关键是化简变形
,
从而使结果能够与
1
比较大小
.
(3)
构造函数法
:
构造函数
,
利用函数的单调性比较大小
.
关键能力学案突破
14
考点一
考点二
考点三
学科素养微专题
考点四
对点训练
1
(1)
已知实数
a
,
b
,
c
满足
b+c
=
6
-
4
a+
3
a
2
,
c-b=
4
-
4
a+a
2
,
则
a
,
b
,
c
的大小关系是
(
)
A.
c
≥
b
>a
B.
a
>
c
≥
b
C.
c
>b>a
D.
a
>c>b
(2)
已知
a
,
b
是实数
,
且
e
b
a
解析
:
(1)
∵
c-b
=
4
-
4
a+a
2
=
(
a-
2)
2
≥
0,
∴
c
≥
b
.
又
b+c
=
6
-
4
a+
3
a
2
,
∴
2
b=
2
+
2
a
2
.
∴
b=a
2
+
1
.
∵
当
x>
e
时
,
f'
(
x
)
<
0,
∴
f
(
x
)
在
(e,
+∞
)
内单调递减
.
∵
e
f
(
b
),
关键能力学案突破
15
考点一
考点二
考点三
学科素养微专题
考点四
不等式的性质及应用
例
2
(1)
如果
a
∈
R
,
且
a
2
+a<
0,
那么
a
,
a
2
,
-a
,
-a
2
的大小关系是
(
)
A.
a
2
>a>-a
2
>-a
B.
a
2
>-a>a>-a
2
C.
-a>a
2
>a>-a
2
D.
-a>a
2
>-a
2
>a
(2)
设
a
,
b
为正实数
.
现有下列命题
:
其中的真命题有
.
(
写出所有真命题的序号
)
D
①④
关键能力学案突破
16
考点一
考点二
考点三
学科素养微专题
考点四
思考
判断多个不等式是否成立常用的方法有哪些
?
解题心得
判断多个不等式是否成立的常用方法
:
方法一是直接使用不等式的性质
,
逐个验证
;
方法二是用特殊值法
,
即举反例排除
.
而常见的反例构成方式可从以下几个方面思考
:(1)
不等式两边都乘一个代数式时
,
要注意所乘的代数式是正数、负数还是
0;(2)
不等式左边是正数
,
右边是负数
,
当两边同时平方后不等号方向不一定保持不变
;(3)
不等式左边是正数
,
右边是负数
,
当两边同时取倒数后不等号方向不变等
.
关键能力学案突破
17
考点一
考点二
考点三
学科素养微专题
考点四
对点训练
2
(1)
已知
a<
0,
-
1
ab
>ab
2
B.
ab
2
>
ab
>a
C.
ab
>a>ab
2
D.
ab
>ab
2
>a
(2)
已知
a
,
b
,
c
∈
R
,
则下列命题中正确的是
(
)
D
C
关键能力学案突破
18
考点一
考点二
考点三
学科素养微专题
考点四
简单不等式的解法
(
多考向
)
考向
1
不含参数的一元二次不等式
例
3
不等式
-
2
x
2
+x+
3
<
0
的解集为
.
思考
如何求解不含参数的一元二次不等式
?
关键能力学案突破
19
考点一
考点二
考点三
学科素养微专题
考点四
考向
2
分式不等式
答案
:
(
-
2,3)
思考
解分式不等式的基本思路是什么
?
关键能力学案突破
20
考点一
考点二
考点三
学科素养微专题
考点四
考向
3
含参数的一元二次不等式
例
5
解关于
x
的不等式
:
x
2
-
(
a+
1)
x+a<
0
.
解
由
x
2
-
(
a+
1)
x+a=
0,
得
(
x-a
)(
x-
1)
=
0,
解得
x
1
=a
,
x
2
=
1
.
当
a>
1
时
,
x
2
-
(
a+
1)
x+a<
0
的解集为
{
x|
1
1}
关键能力学案突破
24
考点一
考点二
考点三
学科素养微专题
考点四
关键能力学案突破
25
考点一
考点二
考点三
学科素养微专题
考点四
一元二次不等式恒成立问题
(
多考向
)
考向
1
不等式在
R
上恒成立求参数范围
例
6
若一元二次不等式
2
kx
2
+kx- <
0
对一切实数
x
都成立
,
则
k
的取值范围为
(
)
A.(
-
3,0] B.[
-
3,0) C.[
-
3,0] D.(
-
3,0)
D
思考
一元二次不等式在
R
上恒成立的条件是什么
?
关键能力学案突破
26
考点一
考点二
考点三
学科素养微专题
考点四
考向
2
不等式在给定区间上恒成立求参数范围
例
7
已知二次函数
f
(
x
)
=ax
2
+x+
1
在区间
[0,2]
上恒有
f
(
x
)
>
0,
求
a
的取值范围
.
解
f
(
x
)
在区间
[0,2]
上恒有
f
(
x
)
>
0,
即
ax
2
>-
(
x+
1)
.
当
x=
0
时
,
对任意的
a
都满足
f
(
x
)
>
0,
所以只需考虑
x
≠0
的情况
.
思考
解决在给定区间上恒成立问题有哪些方法
?
关键能力学案突破
27
考点一
考点二
考点三
学科素养微专题
考点四
考向
3
给定参数范围的恒成立问题
例
8
对任意的
k
∈
[
-
1,1],
函数
f
(
x
)
=x
2
+
(
k-
4)
x+
4
-
2
k
的值恒大于零
,
则
x
的取值范围是
.
答案
:
{
x|x
<
1
或
x>
3}
解析
:
x
2
+
(
k-
4)
x+
4
-
2
k>
0
恒成立
,
即
g
(
k
)
=
(
x-
2)
k+
(
x
2
-
4
x+
4)
>
0
在
k
∈
[
-
1,1]
时恒成立
.
思考
如何求解给定参数范围的恒成立问题
?
关键能力学案突破
28
考点一
考点二
考点三
学科素养微专题
考点四
2
.
含参数的一元二次不等式在某区间内恒成立问题
,
常有两种解决方法
:
一是利用二次函数在区间上的最值来解决
;
二是先分离出参数
,
再通过求函数的最值来解决
.
3
.
已知参数范围求函数自变量的范围的一般思路是更换主元法
.
把参数当作函数的自变量
,
得到一个新的函数
,
然后利用新函数求解
.
关键能力学案突破
29
考点一
考点二
考点三
学科素养微专题
考点四
对点训练
4
(1)
已知
a
为常数
,
任意
x
∈
R
,
ax
2
+ax+
1
>
0,
则
a
的取值范围是
(
)
A.(0,4) B.[0,4) C.(0,
+∞
) D.(
-∞
,4)
(2)
已知函数
f
(
x
)
=x
2
+mx-
1,
若对于任意
x
∈
[
m
,
m+
1],
都有
f
(
x
)
<
0
成立
,
则实数
m
的取值范围是
.
(3)
已知不等式
xy
≤
ax
2
+
2
y
2
对
x
∈
[1,2],
y
∈
[2,3]
恒成立
,
则实数
a
的取值范围是
.
B
[
-
1,
+∞
)
关键能力学案突破
30
考点一
考点二
考点三
学科素养微专题
考点四
关键能力学案突破
31
考点一
考点二
考点三
学科素养微专题
考点四
关键能力学案突破
32
考点一
考点二
考点三
学科素养微专题
考点四
1
.
比较法是不等式性质证明的理论依据
,
是不等式证明的主要方法之一
.
作差法的主要步骤为作差
—
变形
—
判断正负
.
2
.
判断不等式是否成立
,
主要有利用不等式的性质和特殊值验证两种方法
,
特别是对于有一定条件限制的选择题
,
用特殊值验证的方法更简单
.
3
.
简单的分式不等式可以等价转化
,
利用一元二次不等式的解法进行求解
.
4
.
“
三个二次
”
的关系是解一元二次不等式的理论基础
;
一般可把
a<0
的情形转化为
a>0
的情形
.
关键能力学案突破
33
考点一
考点二
考点三
学科素养微专题
考点四
5
.
(1)
对于一元二次不等式恒成立问题,恒大于
0
就是相应的二次函数的图像在给定的区间上全部在
x
轴上方,恒小于
0
就是相应的二次函数的图像在给定的区间上全部在
x
轴下方
.
另外常转化为求二次函数的最值或用分离参数法求最值
.
(2)
解决恒成立问题一定要搞清楚谁是主元,谁是参数
.
一般地,知道谁的范围,谁就是主元,求谁的范围,谁就是参数
.
关键能力学案突破
34
考点一
考点二
考点三
学科素养微专题
考点四
1
.
发散思维训练
——
一题多变练发散
典例
已知函数
f
(
x
)
=mx
2
-mx-
1
.
若对于
x
∈
R
,
f
(
x
)
<
0
恒成立
,
求实数
m
的取值范围
.
解
当
m=
0
时
,
f
(
x
)
=-
1
<
0
恒成立
.
综上
,
-
4
查看更多