内蒙古包钢一中2019-2020学年高二上学期期中考试数学（文）试卷

内蒙古包钢一中2019-2020学年高二上学期期中考试数学（文）试卷

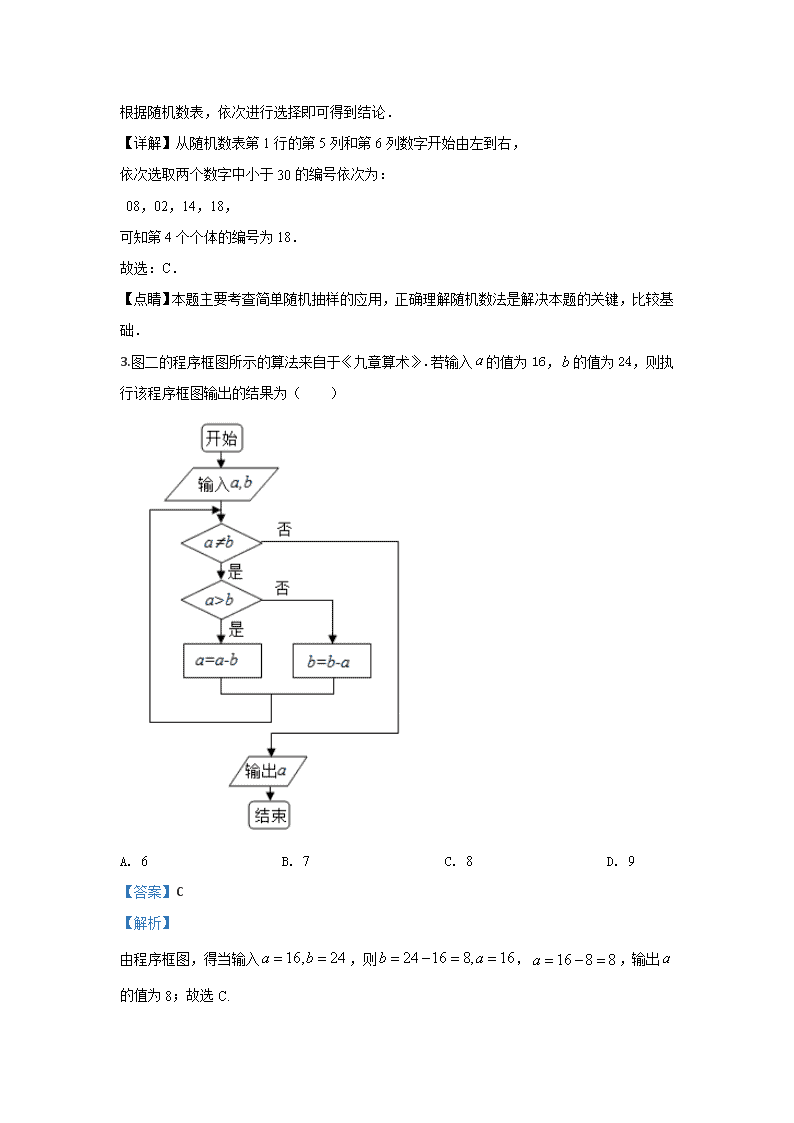
文科数学试卷 注意：本试卷共分为第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）的答案全部答在答题卡上，考试结束后只交答题卡.‎ 第Ⅰ卷 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.若复数满足，其中是虚数单位，则的实部为（ ）‎ A. 2 B. ‎-2 ‎C. 1 D. -1‎ ‎【答案】A ‎【解析】‎ 分析】‎ 把已知等式变形，再由复数代数形式的乘除运算化简得答案．‎ ‎【详解】由，得，‎ 所以的实部为2.‎ 故选：A.‎ ‎【点睛】本题考查复数代数形式的乘除运算，考查复数的基本概念，是基础题．‎ ‎2.总体由编号为01，02，…，29，30的30个个体组成.利用下面的随机数表选取4个个体，选取方法是从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出的第4个个体的编号为（ ）‎ ‎7806‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0247‎ ‎1821‎ ‎9800‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ A. 02 B. ‎14 ‎C. 18 D. 29‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据随机数表，依次进行选择即可得到结论．‎ ‎【详解】从随机数表第1行的第5列和第6列数字开始由左到右，‎ 依次选取两个数字中小于30的编号依次为：‎ ‎ 08，02，14，18，‎ 可知第4个个体的编号为18．‎ 故选：C．‎ ‎【点睛】本题主要考查简单随机抽样的应用，正确理解随机数法是解决本题的关键，比较基础．‎ ‎3.图二的程序框图所示的算法来自于《九章算术》.若输入的值为16， 的值为24，则执行该程序框图输出的结果为（ ）‎ A. 6 B. ‎7 ‎C. 8 D. 9‎ ‎【答案】C ‎【解析】‎ 由程序框图，得当输入，则，，输出的值为8；故选C.‎ ‎4.下列说法正确的是（ ）‎ A. 若残差平方和越小，则相关指数越小 B. 将一组数据中每一个数据都加上或减去同一常数，方差不变 C. 若的观测值越大，则判断两个分类变量有关系的把握程度越小 D. 若所有样本点均落回归直线上，则相关系数 ‎【答案】B ‎【解析】‎ ‎【分析】‎ 由残差平方和越小，模型的拟合效果越好，可判断；由方差的性质可判断；由的随机变量的观测值的大小可判断；由相关系数的绝对值趋近于1，相关性越强，可判断.‎ ‎【详解】对于，可用残差平方和判断模型的拟合效果，残差平方和越小，模型的拟合效果越好，相关指数越大，故错误；‎ 对于，将一组数据的每一个数据都加上或减去同一常数后，由方差的性质可得方差不变，故正确；‎ 对于，对分类变量与，它们的随机变量的观测值越大，“与有关系”的把握程度越大，故错误；‎ 对于，若所有样本点均落在回归直线上，则相关系数，故错误.‎ 故选：B.‎ ‎【点睛】本题考查命题的真假判断，主要是线性回归直线的特点和线性相关性的强弱、样本数据的特征值和模型的拟合度，考查判断能力，属于基础题．‎ ‎5.若从数字1,2,3,4,5中任取两个不同的数字构成一个两位数，则这个两位数大于40的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 从数字1，2，3，4，5中任取两个不同的数字构成一个两位数，‎ 这个两位数大于40,则十位数字为4或5，共有.‎ 概率为.‎ 故选C.‎ 点睛：古典概型中基本事件数的探求方法 ‎(1)列举法.‎ ‎(2)树状图法：适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目，常采用树状图法.‎ ‎(3)列表法：适用于多元素基本事件的求解问题，通过列表把复杂的题目简单化、抽象的题目具体化.‎ ‎(4)排列组合法：适用于限制条件较多且元素数目较多的题目.‎ ‎6.某小组有3名男生和2名女生，从中任选2名学生参加演讲比赛，那么下列对立的两个事件是（ ）‎ A. “至少1名男生”与“至少有1名是女生”‎ B. 恰好有1名男生”与“恰好2名女生”‎ C. “至少1名男生”与“全是男生”‎ D. “至少1名男生”与“全是女生”‎ ‎【答案】D ‎【解析】‎ 从3名男生和2名女生中任选2名学生参加演讲比赛，‎ ‎“至少1名男生”与“至少有1名是女生”不互斥；‎ ‎“恰好有1名男生”与“恰好2名女生”是互斥不对立事件；‎ ‎“至少1名男生”与“全是男生”不互斥；‎ ‎“至少1名男生”与“全是女生”是对立事件；‎ 故选D ‎7.圆心在轴上，且过点的圆与轴相切，则该圆的方程是( )‎ A. B. ‎ C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 本题首先可以根据圆心在轴上且与轴相切设圆的圆心为，再根据过点即可列出方程解出的值，最后得出结果．‎ ‎【详解】由题意，圆心在轴上且过点的圆与轴相切，‎ 设圆的圆心为，半径为．‎ 则，解得 所求圆的方程为，即，故选B．‎ ‎【点睛】本题考查了圆的相关性质，主要考查圆的方程的求解，圆心到圆上的点的距离都是半径是解决本题的关键，考查方程思想，是简单题．‎ ‎8.过点的直线与圆有公共点，则直线的倾斜角的取值范围是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 先设直线点斜式，再根据圆心到直线距离小大于半径得斜率范围，最后根据斜率与倾斜角关系得结果.‎ ‎【详解】由题意得直线斜率存在，设为k，则直线：，‎ 由直线与圆有公共点得，‎ 从而倾斜角取值范围是，选D.‎ ‎【点睛】本题考查直线与圆位置关系、直线倾斜角与斜率关系，考查基本求解能力.‎ ‎9.某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩（均为整数）的频率分布直方图如图,估计这次测试中数学成绩的平均分、众数、中位数分别是（ ）‎ A. 73.3，75，72 B. 72，75，73.3‎ C. 75，72，73.3 D. 75，73.3，72‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据频率分布直方图,结合平均数、众数、中位数的求法,即可得解.‎ ‎【详解】由频率分布直方图可知,‎ 平均数为 ‎ 众数为最高矩形底边的中点,即 中为数为: ‎ 可得 所以中为数为 ‎ 综上可知,B为正确选项 故选:B ‎【点睛】本题考查了频率分布直方图应用,平均数、众数、中位数的计算,属于基础题.‎ ‎10.已知是圆上固定的一点，在圆上其他位置上任取一点，则的长度小于半径的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 先求出当的长度等于半径长度时，然后由圆的对称性及几何概型的概率公式可求出所求．‎ ‎【详解】当的长度等于半径长度时，，‎ 由圆的对称性知，此时，‎ 由几何概型得：.‎ 故选：D.‎ 故选：A.‎ ‎【点睛】本题考查的知识点是几何概型的意义，关键是要找出满足条件的度数，再结合圆的性质，属于基础题．‎ ‎11.一名法官在审理一起珍宝盗窃案时，四名嫌疑人甲、乙、丙、丁的供词如下，甲说：“罪犯在乙、丙、丁三人之中”；乙说：“我没有作案，是丙偷的”；丙说：“甲、乙两人中有一人是小偷”；丁说：“乙说的是事实”．经过调查核实，四人中有两人说的是真话，另外两人说的是假话，且这四人中只有一人是罪犯，由此可判断罪犯是( )‎ A. 乙 B. 甲 C. 丁 D. 丙 ‎【答案】A ‎【解析】‎ ‎【分析】‎ 由题意，这个问题的关键是四人中有两人说真话，另外两人说了假话，通过这一突破口，进行分析，推理即可得到结论.‎ ‎【详解】在甲、乙、丙、丁四人的供词中，可以得出乙、丁两人的观点是一致的，因此乙丁两人的供词应该是同真同假（即都是真话或都是假话，不会出现一真一假的情况）；‎ 假设乙、丁两人所得都是真话，那么甲、丙两人说的是假话，由乙说真话可推出丙是犯罪的结论；‎ 由甲说假话，推出乙、丙、丁三人不是犯罪的结论；显然这两人是相互矛盾的；所以乙、丁两人说的是假话，而甲、丙两人说的是真话，‎ 由甲、丙的供词可以断定乙是犯罪的，乙、丙、丁中有一人是犯罪的，‎ 由丁说假话，丙说真话推出乙是犯罪的，综上可得乙是犯罪的，故选A.‎ ‎【点睛】本题主要考查了推理问题的实际应用，其中解答中结合题意，进行分析，找出解决问题的突破口，然后进行推理是解答的关键，着重考查了推理与论证能力.‎ ‎12.若过原点的动直线将圆：分成两部分的面积之差最大时，直线与圆的交点记为、；直线将圆分成两部分的面积相等时，直线与圆的交点记为、；则四边形的面积为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 根据题意，得出直线将圆分成两部分面积相等即过圆心时，可得为直径，当直线将圆分成两部分面积之差最大，此时，进而求出，再根据，即可算出四边形的面积.‎ ‎【详解】直线将圆分成两部分面积相等即过圆心时，‎ 可得为直径，，‎ 要是分成两部分面积之差最大,‎ 即过原点的弦长最短，弦心距最大，此时,‎ 在中，‎ ‎，则，‎ 那么.‎ 故选：D.‎ ‎【点睛】本题考查直线与圆的位置关系，还考查直线与圆的弦长以及四边形的面积，属于中档题.‎ 第Ⅱ卷 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13.如图所示，半径为4的圆中有一封闭曲线围成的阴影区域.‎ 在圆中随机撒一粒豆子，它落在阴影区域内的概率是，则阴影部分的面积约为_________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 圆中随机撒一粒豆子，它落在阴影区域内的概率是，可得，计算后即可得出结论.‎ ‎【详解】圆中随机撒一粒豆子，它落在阴影区域内的概率是，‎ 所以，‎ 又因为，‎ 所以.‎ 故答案为：.‎ ‎【点睛】本题考查的知识点是根据几何概型的意义进行模拟试验，计算不规则图形的面积，关键是要根据几何概型的计算公式，列出豆子落在阴影区域内的概率与阴影部分面积及圆面积之间的关系．‎ ‎14.甲乙两套设备生产的同类型产品共5600件，采用分层抽样的方法从中抽取一个容量为80的样本进行质量检测，若样本中有50件产品由甲设备生产，则乙设备生产的产品总数为_______件.‎ ‎【答案】2100‎ ‎【解析】‎ ‎【分析】‎ 根据样本容量为80，可得抽取的比例，再求得样本中由乙设备生产的产品数，即可得出乙设备生产的产品总数.‎ ‎【详解】已知甲乙产品总数为5600，样本容量80，‎ 所以抽取比例为：，‎ 因为80件样本中，有50件产品由甲设备生产，‎ 则有30件产品由已设备生产，‎ 所以乙设备生产产品总数为.‎ 故答案为：2100.‎ ‎【点睛】本题考查了分层抽样方法，熟练掌握分层抽样方法的特征是解题的关键．‎ ‎15.某单位有840名职工，现采用系统抽样方法抽取42人做问卷调查，将840人按1，2，…，840随机编号，若第八组抽得的号码为144，则在第三十组中抽得的号码是________.‎ ‎【答案】584.‎ ‎【解析】‎ ‎【分析】‎ 根据系统抽样的定义，确定抽样的间距，利用等差数列的通项公式，即可求出结论．‎ ‎【详解】因为从840人中抽取42人，所以抽取的间距为，‎ 即号码构成公差的等差数列，‎ 设抽到的第一组号码为，各组抽取号码为，‎ 所以各组抽取的号码为：，‎ 由于第八组抽得的号码为144，即，‎ 即，解得，‎ 则在第三十组中抽得的号码是：.‎ 故答案为：584.‎ ‎【点睛】本题主要考查系统抽样的定义，还运用了等差数列的通项公式，利用条件确定系统抽样的组距是解决本题的关键．‎ ‎16.如图甲是第七届国际数学教育大会（简称）的会徽图案，会徽的主体图案是由如图乙的一连串直角三角形演化而成的，其中，如果把图乙中的直角三角形继续作下去，记的长度构成数列，则此数列的通项公式为_____．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 由图可知，由勾股定理可得,利用等差数列的通项公式求解即可.‎ ‎【详解】根据图形，‎ 因为都是直角三角形，‎ ‎,‎ 是以1为首项，以1为公差的等差数列，‎ ‎，‎ ‎，故答案为.‎ ‎【点睛】本题主要考查归纳推理的应用，等差数列的定义与通项公式，以及数形结合思想的应用，意在考查综合应用所学知识解答问题的能力，属于与中档题.‎ 三、解答题（本大题共6小题，共70分）‎ ‎17.已知圆的方程为，求过点的圆的切线方程.‎ ‎【答案】或.‎ ‎【解析】‎ ‎【分析】‎ 由圆的方程找出圆心坐标与半径，分两种情况考虑：若切线方程斜率不存在，直线满足题意；若斜率存在，设出切线方程，根据直线与圆相切时圆心到切线的距离，求出 的值，综上即可确定出满足题意的切线方程；‎ ‎【详解】由圆的方程得到圆心，半径，‎ 当直线斜率不存在时，方程与圆相切；‎ 当直线斜率存在时，设方程为，即，‎ 由题意得：，解得：，‎ ‎∴方程为，即，‎ 则过点的切线方程为或.‎ ‎【点睛】本题考查了直线与圆相交的性质，涉及的知识有：点到直线的距离公式，垂径定理，勾股定理，以及圆的标准方程，利用了分类讨论的思想，熟练掌握定理及公式是解本题的关键．‎ ‎18.甲、乙两位同学参加数学竞赛培训，现得到他们在培训期间参加的8次比赛成绩如下：甲：81，79，95，88，84，93，78，82；乙：80，83，92，85，75，95，80，90.‎ ‎（1）试画出甲、乙两位同学比赛成绩的茎叶图，你能从茎叶图中获取哪些信息？（不少于三条）‎ ‎（2）在甲同学的8次比赛成绩中，从不小于80分的成绩中随机抽取2个成绩，列出所有可能的结果，并求抽出的2个成绩均大于85分的概率.‎ ‎【答案】（1）见解析；（2）结果见解析，所求的概率是.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用所给数据，即可画出甲、乙两位学生成绩的茎叶图；由茎叶图可得出学生甲成绩的中位数和学生乙成绩的众数；根据乙的数据，可求出学生乙成绩的平均数；‎ ‎（2）从甲同学超过80分的6个成绩中任取两个，基本事件共15个，抽出的2个成绩均大于85分，共3个，即可求抽出的2个成绩均大于85分的概率．‎ ‎【详解】（1）根据题意，画出茎叶图如下：‎ 由茎叶图可知，甲成绩的中位数为83，乙成绩的众数为80，‎ 学生乙成绩的平均数为：.‎ ‎（2）从不小于80分的成绩中抽取2个成绩，所有结果为：‎ ‎，，，，，，，，‎ ‎，，，，，，，共15个，‎ 其中，满足2个成绩均大于85分的有，，共3个，‎ 故所求的概率是.‎ ‎【点睛】本题考查茎叶图，以及根据茎叶图求中位数、众数、平均数，还考查利用列举法求古典概率，同时考查学生分析解决问题的能力．‎ ‎19.随着我国经济的发展，居民的储蓄存款逐年增长.某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ 时间代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎（1）求关于的回归方程；‎ ‎（2）试预测该地区在建国一百周年时的的储蓄存款，并求关于的回归方程.‎ 附：，.‎ ‎【答案】（1）；（2），当时，千亿元.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先求出和，根据公式求得和的值，即可求出线性回归方程；‎ ‎（2）由，先算出求关于的回归方程，代入时，可预测该地区在建国一百周年时的的储蓄存款.‎ ‎【详解】（1）由题意，，，‎ ‎，，‎ ‎∴，，‎ ‎∴关于的回归方程；‎ ‎（2）由题可知，，‎ ‎，‎ 即，‎ 所以当时，千亿元.‎ ‎【点睛】本题考查线性回归方程的求法，考查计算能力，是中档题．‎ ‎20.（1）求证：当，，为正数时，；‎ ‎（2）已知，，求证.‎ ‎【答案】（1）见解析；（2）见解析.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）将所证不等式的左端展开，重新组合，利用基本不等式即可证得结论成立；‎ ‎（2）分别化简左右两边，得左边，右，要证 ‎，即证，同时运用同角三角函数关系化简，即可证明.‎ ‎【详解】（1）证明：左边，‎ 因为、、为正数，‎ ‎∴左边，‎ 当且仅当时取等号.‎ ‎∴.‎ ‎（2）左，右，‎ 要证，只需证，‎ 即证，‎ 即证，‎ 而，所以原方程成立.‎ ‎【点睛】本题考查不等式的证明，着重考查基本不等式的应用，考查分析法、综合法，考查推理证明能力，属于中档题．‎ ‎21.为了解某高校学生中午午休时间玩手机情况，随机抽取了100名大学生进行调查.下面是根据调查结果绘制的学生日均午休时间的频率分布直方图，将日均午休时玩手机不低于40分钟的学生称为“手机控”.‎ ‎（1）求列联表中未知量的值；‎ 非手机控 手机控 合计 男 女 ‎10‎ ‎55‎ 合计 ‎（2）能否有把握认为“手机控与性别有关”？‎ ‎.‎ ‎0.05‎ ‎0.10‎ ‎3.841‎ ‎6.635‎ ‎【答案】（1），，，；（2）没有把握认为“手机控”与性别有关.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由频率分布直方图能求出在抽取的100人中，可算出“手机控”人数，因而得出“非手机控”的人数，即可算出.‎ ‎（2）求出2×2列联表，假设：“手机控”与性别没有关系，求出，从而得到没有95%把握认为“手机控”与性别有关．‎ ‎【详解】（1）由频率分布直方图可知，在抽取的100人中，‎ ‎“手机控”有：人，非手机控75人，‎ ‎∴，，，；‎ ‎（2）从而列联表如下：‎ 非手机控 手机控 合计 男 ‎30‎ ‎15‎ ‎45‎ 女 ‎45‎ ‎10‎ ‎55‎ 合计 ‎75‎ ‎25‎ ‎100‎ 假设：“手机控”与性别没有关系.‎ 将列联表中的数据代入公式，计算得：，‎ 当成立时，，‎ ‎∴，所以没有把握认为“手机控”与性别有关.‎ ‎【点睛】本题考查独立性检验的应用，还涉及频率分布直方图求频数，考查学生的计算能力.‎ ‎22.在平面直角坐标系中，已知圆：，点，过点的直线交圆于、两点.‎ ‎（1）试判断直线：与圆的位置关系；‎ ‎（2）设弦的中点为，求的轨迹方程.‎ ‎【答案】（1）直线与圆相交；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）由直线：可知过定点，求圆心到的距离，与半径2比较，通过判断点和圆的位置关系，即可得出直线与圆的位置关系；‎ ‎（2）分类讨论，当点与点不重合时，利用圆的性质得出，运用向量垂直的坐标运算，即可得出的轨迹方程；当点与点重合，即，时，也满足上式；综合得出轨迹方程.‎ ‎【详解】（1）由圆的方程可知，圆心，半径为2，‎ 因为直线过定点，且，‎ 所以点在圆内，故直线：与圆相交.‎ ‎（2）由圆的性质知：当点与点不重合时，‎ 则，​∴，‎ 设，则，，‎ 则.‎ 当点与点重合，即，时，也满足上式.‎ ‎∴点的轨迹方程为.‎ ‎【点睛】本题考查直线与圆的位置关系和轨迹方程，还利用点与圆的位置关系、圆的性质、向量垂直的坐标运算，同时考查分析能力和转化思想.‎ ‎ ‎